
- •Кафедра начертательной геометрии и графики
- •Лекция 1 введение
- •Из истории предмета
- •Методы проецирования
- •Основные системы изображений, получаемые при помощи проецирования
- •Ортогональный чертеж. Проецирование точки
- •Октанты
- •Знаки прямоугольных координат в различных октантах
- •ТочкА на прямой
- •Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
- •4) Осевая плоскость.
- •Плоскости, параллельные двум осям координат
- •Прямые частного положения в плоскости
- •Лекция 5
- •6 (Ac). Прямая, перпендикулярная плоскости
- •Взамно перпендикулярные плоскости
- •Основы линейной перспективы. Сущность метода.
- •Система плоскостей линейной перспективы
- •Перспективы точек, расположенных в различных частях пространства.
- •Перспектива прямой линии.
- •Взаимное положение прямых Параллельные прямые
- •Пересекающиеся и скрещивающиеся прямые
- •Выбор точки и угла зрения. Ориентировка картины
- •Методы построения перспективы радиальный метод
- •Метод архитекторов
- •Лекция 7 аксонометрические проекции
- •Аксонометрические проекции
- •Вместо заключения: начертательная геометрия и машинная графика
- •Дополнительный
- •Оглавление
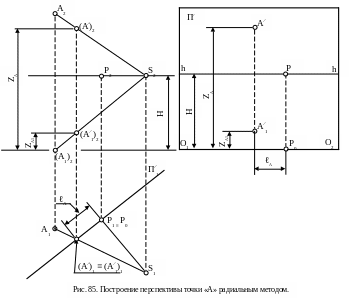
Методы построения перспективы радиальный метод
Сущность этого метода заключается в определении точек пересечения лучей с картинной плоскостью (рис. 85).
Перспектива А/ и вторичная проекция А/1 точки А на плоскости картины П/ строятся на координатах ZA, ZA1 и ℓA. Координаты ZA и ZA1 – это высотные отметки (расстояние от предметной плоскости) фронтальных проекций (А/)2 и (А/1)2 точек пересечения проекционных лучей S2А2 и S2(А1)2 из точки зрения S на точку А и ее горизонтальную проекцию А1 с плоскостью картины. Координата ℓA – это расстояние на плане (в предметной плоскости) между линией РР0 и проекцией линии пересечения лучевой плоскости на точку А с плоскостью картины.
Метод архитекторов
Данный метод построения перспективы основан на использовании точек схода параллельных прямых.
Сущность рассматриваемого метода может быть показана на примере построения перспективы фигуры, расположенной на горизонтальной плоскости
(рис. 86):
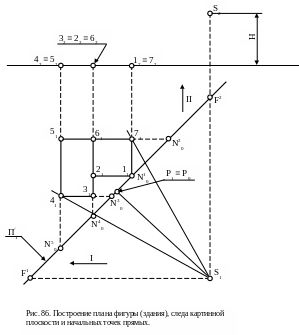
строится план фигуры (например, план фасада здания);
с учетом вышеуказанных рекомендаций определяются положения следа картинной плоскости П∕1, точки зрения S (S1, S2) и главной точки P (P1 ≡ P0) на плане;
л
 инии
контура плана могут быть разделены на
два пучка параллельных пря-
инии
контура плана могут быть разделены на
два пучка параллельных пря-
мых (направления I и II). Определяются перспективы несобственных точек (F11 и F12) каждого из пучков. Точка F11 является перспективой несобственной точки пучка параллельных прямых направления I, а точка F12 является перспективой несобственной точки пучка параллельных прямых направления II. Обе точки найдены при помощи лучей S1F11 и S1F12, параллельных соответственно направлениям Iи II;
в качестве вторых точек для построения перспективы каждой из прямых используются характерные точки, в которых эти прямые пересекают плоскость картины, т.е. начальные точки прямых ( точки N10, N20, N30, N40, N50,);
полученные точки с плана (рис. 86) с учетом масштаба построения перспективы переносятся на картину (рис. 87). При этом точки F1 , F2 и Р откладываются на линии горизонта (h - h), а точки N10, N20, N30, N40, N50 на линию основания картины (О1 – О2). Расстояние между линией горизонта (h - h) и линией основания картины (О1 – О2) принимается равным высоте расположения точки зрения S – H (с учетом масштаба). Строятся перспективы прямых, пересечения которых определяют вершины заданного контура. Так, точка пересечения прямых N30 F1 и N40 F2 представляют собой перспективу точки 3. Аналогично находятся остальные точки.
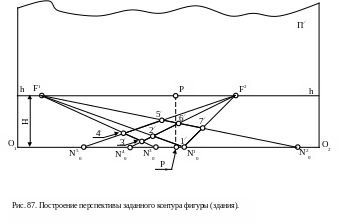
Итак, каждая точка плоской фигуры определяется пересечением прямых, принадлежащих двум различным пучкам параллельных линий.
Построение перспективы предмета (например, здания) проводится с изменением всех линейных размеров с учетом принятого масштаба.
После того, как начерчены ортогональные проекции фасада и плана здания (рис. 88) и построена перспектива контура плана здания (см. пример построения пер-
с пективы
контура – рис. 87), построение перспективы
здания осуществляется в такой
последовательности (рис. 89):
пективы
контура – рис. 87), построение перспективы
здания осуществляется в такой
последовательности (рис. 89):
через вершины (точки 1/, 2/, 3/ и т.д.) проводятся тонкие вертикальные прямые (будущие ребра здания);
от точки 1/ на проходящей через нее вертикали откладывается отрезок 1/ - А/ длиной Н1, умноженный на масштаб. Поскольку ребро А лежит в плоскости картины, высота этого ребра является истинной величиной;
ч
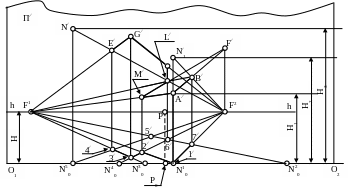
Рис. 89. Построение перспективы здания.
ерез точку А/ проводится прямая в точку схода следов F1. На этой прямой в точке пересечения с вертикалью 2/ - М/ находится точка М/;для того, чтобы получить перспективы вертикальных ребер высотой Н3, проходящих через точки 3/, 4/, 5/, и 6/, необходимо соответственно на вертикалях из точек N40, N50, N20, или N30, отложить отрезок, равный Н3, умноженный на масштаб. Из точек F1 и F2 через полученные точки проводятся прямые и там, где соответствующие прямые (например, F2N/ и F1G/) пересекут вертикали из точек 3/, 4/, 5/ и 6/ строятся верхние точки ребер (например, E/ и G/), а соответственно и перспективы самих ребер.
Аналогично производится построение ребер высотой Н2.
Проверкой точности построения является сходимость прямых A/B/и M/L/на вертикали, проведенной через точку сходаF2 (в точке F/).
