15 Предельные теоремы Лапласа и Пуассона. Геометрические вероятности

Впервые предельная теор. Была сформул. Муавром в 1730 г., когда p=q=1/2.

Локальная теорема Муавра-Лапласа:

Если вер-ть наступления нек-го соб. А в n независимых испытаниях постоянна и равна p (0<p<1), то вер-ть того, что в этих испытаниях соб.А наступит ровно m раз, удовлетворяет след.соотношению:

, где .

Из теоремы следует, что при больших значениях n→∞, правая часть стемится к 1.

.

Очевидно, что φ(x) четн.ф-я, т.е. φ(-x)= φ(x). Значение φ(x) табулировано.

Вторая ф-ла Лапласа дает приближенное выражение для вер-ти того, что число наступления события А в n опытах окажется заключенным в некотором отрезке.

Интегральная теорема Лапласа:

Если вер-ть появления сою.А в каждом испытании постоянна и равна p, то вер-ть того, что соб.А наступит в n испытаниях от k₁ до k₂ раз, определяется формулой:

.

, .

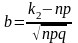- ф-я Лапласа, она не выражается в элементарных функциях

12 Схема независимых испытаний Бернулли

Серия повторных независимых испытаний, в каждом из которых данное событие имеет одну и ту же вероятность , не зависящую от номера испытания, называется схемой Бернулли. Одинаково независимые между собой испытания в каждом из которых событие А, наступающее с положительной вероятностью p, рассматривается в границах опыта S наз испытанием Бернулли. Таким образом, в схеме Бернулли для каждого испытания имеются только два исхода: событие (успех), вероятность которого и событие (неудача), вероятность которого .

Условия схемы Бернулли:

число испытаний конечно

испытания независимы

вероятность наступления события А постоянна в каждом испытании.

- формула Бернулли . А сами испытания называются биномиальными .

Биномиальный закон распределения вероятностей задается 2 параметрами:

вероятностью успеха р

числом испытаний n

число n и p в схеме Бернулли играет следующую роль: одно из двух ближайших к нему целых чисел является наиболее вероятным числом успехов.

Условимся для краткости n –кратное повторение опыта называть серией. Пусть мы производим N серий, где в первой серии А наступило k1 раз, во второй k2 … N-ой kn раз. Составим среднеарифметическое числа успехов

13 Если СВ Х принимает значения Х=0,1,2,…,m,…,n с вероятностью

_m

P_п(m)=С_nр^mq^{n –m} , то говорят,что СВ Х распределена по биноминальному закону.

Схема Бернулли повторных независимых испытаний с вероятностью р=р(А) и q=1-p

Рассмотрим формулу Бинома Ньютона:

_{0 1 m}

(p+q)ⁿ=C_np⁰qⁿ+C_np¹q^n-1+…+ C_n

_n

p^mq^n-m+…+C_npⁿ

Составим ряд распределения биноминального закона:

Х	0	1	…
Р	q^n	1 C	….

Числовые характеристики биноминального закона.

1. М(Х)=np, 2)D(X)=npq 3) σ(X)=√npq

Док-во:

1. Х—число появлений события А в n опытах как сумму n независимых СВ:

Х=Х₁+Х₂+…+Х_n , где Х_і—число появлений события А в і-ом опыте. Х_і={0;1}

Хі	0	1
Р	q	p

М(Х)=0*q+1*p=p

_n

М(Х)=М(Х₁+Х₂+…+Х_n)=∑М(Х_і)=

^і=1

р+р+р+...+р(n раз)=np

2. D(Х)=М(Х²)-(М(Х))²

Хі^2	0^2	1^2
Р	q	p

М(Х_і²)=0²*q+1²*p=p

М(Х²)=np

D(Х_і)=М(Х²_і)-(М(Х_і))²

D(Х_і)=р-р²=p(1-p)=pq

D(Х)=D(Х_і+...+Х_n)=D(Х₁)+D(Х₂)+

_{n n}

…+D(Х_n)=∑D(Х_і)=∑pq=npq

^{і=1 і=1}

3. σ(Х)=√D(Х)=√npq

М(Х)=np

D(Х)=npq

σ(Х)=√npq

14 ЗАКОН ПУАССОНА.

Пусть СВ Х принимает значения:

Х=0,1,2,…,m,…

P(X=m)=P_n(m)=(e^-λ λ^m)/m!

Р-вероятн появл соб А в одном из n независ испыт, когда n достат велико, а р-мало. λ=nр

Запиш ряд распред СВ Х, котор будет назыв закон Пуассона

Х	0	1	2
Р	e^-^λ	e^-^λ/1!	e^-^λ λ^2/2!
Х	…	m	…
Р	…	e^-λ λ^m/m!	…

_∞

с

_∞ ^∞

= e^-λ∑ (m-1)λ^m/(m-1)!+ e^-λ∑ λ^m/

^{m=1 v=1}

_∞

/(m-1)!= e^-λ∑ λ^m-2 λ²/(m-2)!+

^m=2

_{∞ ∞}

+ e^-λ∑ λ^m/(m-1)!= e^-λλ²∑ λ^m-2/(m-

^{m=1 m=2}

_∞

2)!+ e^-λλ∑ λ^m-1/(m-1)!= e^-λ λ²* e^λ+

^m=1

+ e^-λ λ* e^λ= λ²+ λ

М(Х²) = λ²+ λ

D(Х)=М(Х²)-(М(Х))²= λ²+ λ- λ²= λ

D(X)=M(X)= λ

3. σ(Х)=√ D(Х)=√λ , ч.т.д.

Замечание: закон Пуассона завис от одн парам λ; биномин закон завис от n,p.

B(n;p)