Распределённых по закону Пуассона

M(x)=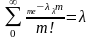

D(x)=M(x²)-(M(x))²

M(x²)=

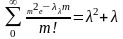
D(x)=M(x²)-(M(x))²=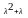 - 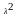= 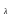(+см. п. 30)

В законе Пуассона мат. Ожидание равно дисперсии M(x)=D(x)=λ

Закон Пуассона зависит от одного параметра λ, биномиальный закон зависит от n , p

17 Равномерное распределение. Числовые характеристики и функция распределения.

Пусть НСВ Х имеет плотность распределения f(x),

1. Мат. Ожидание M(X)=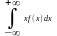 (1); 2. Дисперсия D(x)= 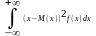(2)

также дисперсию можно находить по ф-ле: D(x)=M(x²)-(M(x))² D(x)=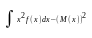 (3)

при этом все несобств. Интегралы предполаг-ся абсолютно сходящимися. В противном случае числовых хар-к у раких СВ не существует.

Равномерное распределение:

Непр. СВ Х наз-ся распределённой по равеномерному з-ну, если плотность её распределения имеет вид:

f(x)={ 0, x<a;

c=const, a<=x<=b

0, x>b

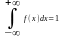
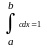
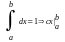=1 c(b-a)=1 c=1/(b-a)

f(x)={ 0, x<a;

1/(b-a), a<=x<=b

0, x>b

M(x)=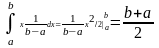

D(x)=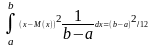

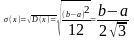
M(x)=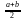 ; D(x)=(b-a)²/12; 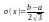; F(x)= ,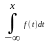

1) x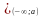 F(x)=0; 2) x 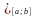F(x)=(x-a)/(b-a); 3) x 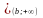F(x)=1

F(x)={ 0, x<a;

x-a/(b-a), a<=x<=b

1, x>b

11 Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством Где f ( x ) дифференциальная функция. Предполагается, что интеграл сходится абсолютно.

В частности, если возможные значения принадлежат интервалу ( a , b ), то Модой М0(Х) непрерывной случайной величины называют то ее возможное значение, которому соответствует максимум дифференциальной функции.

О.Медианой Me(X) непрерывной случайной величины называют то ее возможное значение, которое определяется равенством Р ( Х < Me(X) )=P(X> Me(X)). .Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством Или равносильным равенством В частности, если возможные значения принадлежат интервалу ( a , b ), то

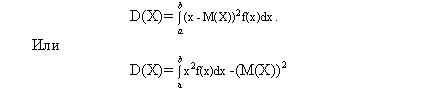
23 Теорема (збч в форме Чебышова)

Если последовательность независимых СВ 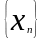имеет конечное значение мат. ожиданий ,а дисперсии этих СВ ограничены одной и той же константой, то данная последовательность удовлетворяет ЗБЧ.

Эта теорема утверждает, что среднеарифметическое больного числа независимых СВ утрачивает характер случайности и сходится по вероятности к постоянному числу.

Неравенство Маркова.

Теор.: Если СВ x принимает только неотрицательные значения, то для любого 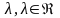справедливо .

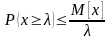Неравенство Чебышова.

Для любой СВ – x имеющей конечное значение дисперсии .

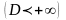При любом сколь угодно малом 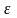(эпсилон) справедливо неравенство

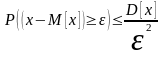Неравенство показывает, что если дисперсия мала по сравнению с 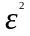и практически можно пренебречь с возможностью осуществления события

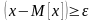, то малой будет и сама величина .

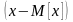Неравенство Чебышова имеет ограниченное значение для практики, т. К. Даёт грубые оценки, но оно служит основой док-ва многих предельных теорем ТВ.

22 Известно, что если случайная величина X задана плотностью распределения о вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова: Пусть случайная величина X распределена по нормальному закону. Тогда Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную отсюда Найдем новые пределы интегрирования. Если ,то ,если ,то тогда Выражение входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем где Ф(x) = ряд … C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.

Отметим ряд свойств функции Лапласа, полезных для применения.

1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).

2. Функция Ф(x) – возрастающая, быстро приближающаяся к своему пределу, равному 0,5: Ф(0) = 0, Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986, Ф(4) = 0,4999 и т.д. На практике полагают Ф(x) для x>5.

L]iuqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqfffffffffffffffffffffffffffffffffffffffffffffffffffffffff67ee444