Вариант 9.
1. В декартовой прямоугольной системе координат даны вершины пирамиды , C1, D1. Найдите:
а) длину ребра ;
б) косинус угла между векторами и ;
в) уравнение ребра ;
г) уравнение грани С1;
если
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
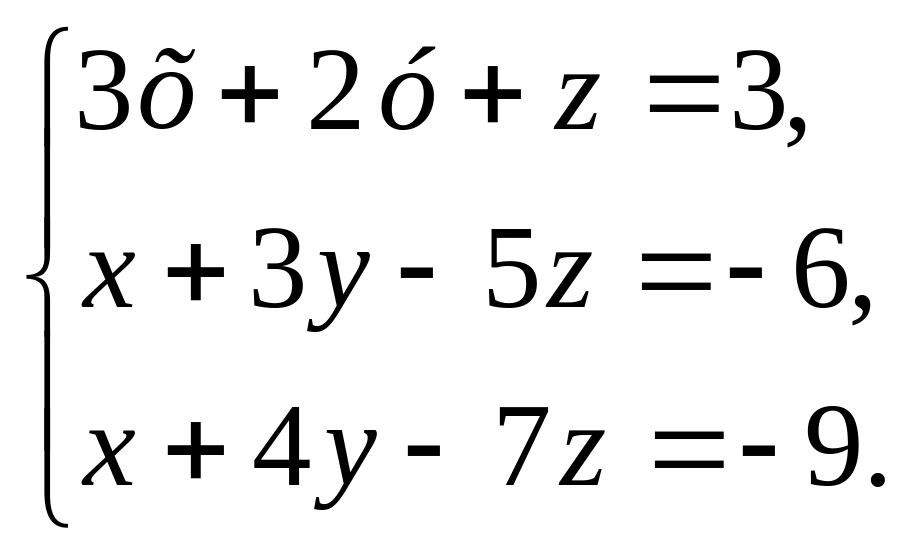
3. На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а). Все выбранные булочки с изюмом; б). Только одна булочка с изюмом.
4. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
5. Задан закон распределения дискретной случайной величины X:
-
Х
-2
-1
0
1
2
3
4
р
0,08
0,1
0,14
0,1
1
0,1
0,1
р
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение данной случайной величины;
в) функцию распределения F(x) и построить ей график;
г) закон
распределения случайной величины
,
если её значения заданы функциональной
зависимостью
6. Установлено, что третья часть покупателей, при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина:
а) ровно 50 человек приобретут товар;
б) от 100 до 120 человек приобретут товар?
Методические рекомендации к выполнению контрольной работы Векторная алгебра и элементы аналитической геометрии
Для решения задачи 1 и задачи 2 необходимо изучить следующую литературу:
Глава 3, стр. 63-74,
Глава 4, стр. 95-101
Глава 9. § 1-13. Стр. 222-251
Теперь рассмотрим применение изученных формул на примерах.
ЗАДАЧА 1.
В
декартовой прямоугольной системе
координат даны вершины пирамиды
.
Найдите:
а) длину ребра ;
б)
косинус
угла между векторами
и
;
в) уравнение ребра ;
г) уравнение грани С1;
если
Решение.
а
)
Найдем координаты вектора А1В1 по формуле
где
- координаты точки А1,
-координаты
точки В1.
Итак
={1-(-2);-3-2;0-2}={3;-5;-2}. Тогда
=
=
.
Итак,
длина отрезка,
(или
длина вектора
)
равна
.
Это и
есть
искомая длина
ребра.
б)
Координаты
={3;-5;-2}
уже известны, осталось определить
координаты вектора
={6-
(-2); 2 - 2; 4 - 2}= {8,0; 2}.
Угол между векторами и вычислим по формуле
cos
φ
=
г де скалярное произведение векторов А1В1 и А1С1 равно ( , )=3·8+(-5)·0+(-2)=24+0-4=20,
=
,
=
=
.
Итак, cos φ = 20 = 10
·
в) Координаты точки А1(-2,2,2) обозначим соответственно Х0 = -2, У0 = 2, Z0 = 2, а координаты точки В1(1,-3,0) через X1 = 1, У1 = -3, Z1 = 0 и воспользуемся уравнением прямой и пространстве, проходящей через две точки:
.
Следовательно, уравнение ребра имеет вид
.
г) Обозначим координаты векторов , и через Х1=3, У1= -5, Z1= -2 и Х2=8, У2= 0, Z2=2 соответственно. Векторное произведение данных векторов определяется формулой
·A1C1 = {Y1·Z2-Y2·Z1;Z1·X2-Z2·X1;X1·Y2-X2·Y2} =
= {(-5)·2-0·(-2);-2·8-2·3;3·0-8·(-5)}={-10,-22,40}
Так как данный вектор перпендикулярен грани С1, то можно воспользоваться уравнением плоскости, проходящей через точку (Х0 У0, Z0) перпендикулярно вектору {А;В;С}, которое имеет вид A·(X-X0)+B·(Y-Y0)+С·(Z-Z0)=0.
Подставим координаты точки А1 (Хо= -2, У0=2, Z0=2) и координаты перпендикулярного вектора А= -10, В= -22, С=40 в это уравнение:
- 10 ( X + 2 ) - 22 (У – 2) т 40 ( Z- 2) - 0. Раскроем скобки и приведем подобные члены - 10 х -22 у + 40z + (-20 + 44-80)=0. Итак, уравнение грани ,C1 имеет вид: -10х- 22у + 4О z-56=0 или -5х- lly + 20z-28=0.