
- •Пермский институт (филиал) фгбоу впо
- •Математика
- •Часть 2: Высшая математика
- •Предисловие и общие рекомендации студенту-заочнику по работе над курсом
- •Чтение учебной литературы.
- •Решение задач.
- •Самопроверка.
- •Консультации.
- •Контрольные работы.
- •Лекции и практические занятия.
- •Зачет и экзамен.
- •Список рекомендуемой литературы. Основная литература
- •4. Высшая математика для экономистов (под ред. Проф. Н.М.Кремера). – м.: Банки и биржи, издательское объединение юнити, 1998
- •Дополнительна литература
- •1. Данко п.Е., Попов я.Г., Кожевникова т.Я. Высшая математика в упражнениях и задачах. Ч. I, II – м.: Высшая школа, 1990.
- •Справочники
- •Правила выбора варианта контрольной работы, ее оформление и зачета
- •Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
- •При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.
- •Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Методические рекомендации к выполнению контрольной работы Векторная алгебра и элементы аналитической геометрии
- •Глава 3, стр. 63-74,
- •Глава 4, стр. 95-101
- •Глава 9. § 1-13. Стр. 222-251
- •Задача 2.
- •Элементы теории вероятности и математической статистики
- •Задача 3.
- •Задача 4.
- •Задача 5.
- •Задача 6.
- •Вопросы к экзамену (за два семестра)
Задача 2.
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;

Решение.
а) Решим данную систему уравнений с помощью формул Крамера (см.[2] глава 10. стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:

Решение.
а) Решим данную систему уравнений с помощью формул Крамера ( см. [2] глава 10, стр. 268).
Тогда
![]() ,
где
,
где

Так
как Δx=
-60; Δy=
-60; Δz=60;
Δ=
-120, то x=![]() ;
y=
;
z=
;
y=
;
z=![]() .
.
6) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнении приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения, легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.
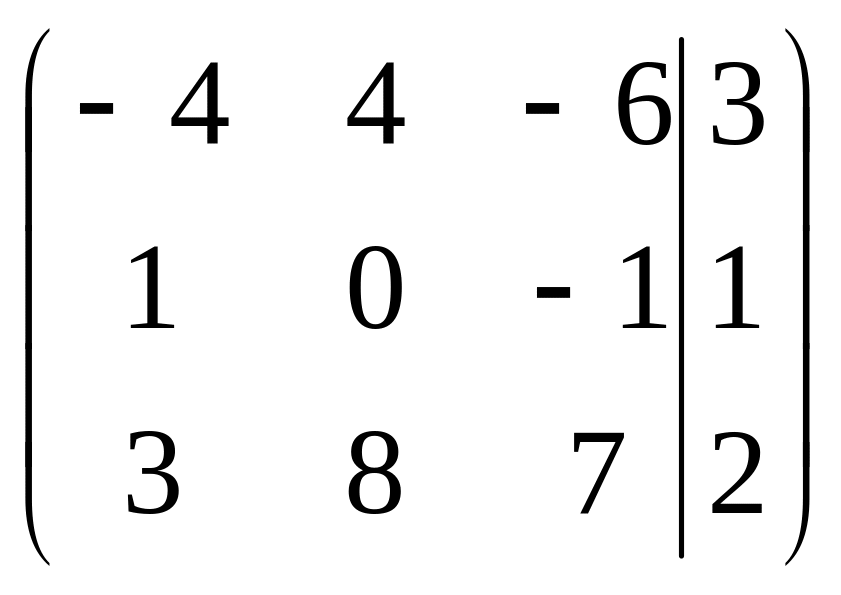
Поменяем местами первую и вторую строки матрицы, чтобы в ее левом верхнем углу была единица. Получим матрицу.

Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид.

Умножим каждый элемент первой строки матрицы на -3. и прибавим полученные числа к соответствующим элементам третьей строки. Получим:

Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.

Умножим каждый элемент второй строки матрицы на -8 и прибавим полученные числа к соответствующим элементам третьей строки:

Данная
матрица соответствует системе уравнений
![]() ,
решение которой совпадает с решением
исходной системы. Начинай с последнего
уравнения, несложно найти все
,
решение которой совпадает с решением
исходной системы. Начинай с последнего
уравнения, несложно найти все
неизвестные.
![]() Действительно,
так как z=
Действительно,
так как z=![]() =
и y
=
и y![]() z=
z=![]() ,
то y
·
,
то y
·
Отсюда,
y
-![]() =
=![]() =
=![]() =
.
Из x-z=1
имеем =z+1=
+1=
=
.
Из x-z=1
имеем =z+1=
+1=
Ответ: x= , y= , z= .
Элементы теории вероятности и математической статистики
Для решения задачи 3 см. [5] глава 1. § 1—5.
Задача 3.
На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги, Вычислить вероятность того, что среди них;
А) нет упаковок с бумагой более низкого качества,
Б) есть одна упаковка такой бумаги.
Решение.
Рассмотрим два случайных события:
А – среди взятых трех упаковок нет упаковок с бумагой более низкого качества;
В - среди взятых трех упаковок есть одна упаковка с бумагой более низкого качества (и, следовательно, две – с бумагой более высокого качества).
Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть
![]() =
=![]() =
=![]() =
=![]() =13·9·28=3276
– числу сочетаний из 28 элементов по 3.
=13·9·28=3276
– числу сочетаний из 28 элементов по 3.
а) Подсчитаем число исходов, благоприятствующих интересующему нас событию (нет упаковок с бумагой более низкого качества). Это число исходов ровно числу способов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть
=![]() =
=![]() =
=![]() =11·23·8=2024
=11·23·8=2024
искомая вероятность равна отношению числа исходов, благоприятствующих событию А, к числу всех элементарных исходов:
Р(А)=![]() =
=![]() ≈0,62
≈0,62
б)
Подсчитаем число исходов,
благоприятствующих
данному событию (среди трех упаковок
бумаги
ровно 1 упаковка
содержит
бумагу
более
низкого
качества): две упаковки
можно
выбрать из 24 упаковок:
![]() =
=![]() =
=![]() =
=![]() =276
способами,
при этом одну упаковку нужно выбирать
из четырех:
=276
способами,
при этом одну упаковку нужно выбирать
из четырех:
![]() =
=![]() =
=![]() =4
способами.
Следовательно,
число
благоприятствующих исходов равно
=4
способами.
Следовательно,
число
благоприятствующих исходов равно
![]() ·
=276·4=1104
·
=276·4=1104
Искомая вероятность
равна отношению числа исходов,
благоприятствующих событию В, к числу
всех элементарных исходов
Р(В)= =
=![]() ≈0,34
≈0,34
Ответ: а)Р(А) =0,62; б) Р(В)=0,34.
