Короткі відомості з теорії та приклади розв’язання задач

Визначення нелінійного рівняння

F(x)=0, де F(x) –функція, нелінійна щодо невідомого.

Приклади :

а) e^{x +2}-ln(x)+5=0 ;

б) sin(x+5) -tg2(x) -7=0 ;

в) x⁵-4x⁴+3x²-10=0.

Вирішити нелінійне рівняння – знайти значення х для якого F(x)=0.

2.1. Метод простих ітерацій (знаходження кореня рівняння x = f(x))

Дано : F(x)=0, x0  а ; b

Метод простих ітерацій заснований на представленні рівняння F(x)=0 у вигляді :x=f(x) та багатократному вживанні формули xn+1= f(xn) до тих пір, поки дотримується умова | xn+1- xn| ≤ε , де ε – задана погрішність обчислення кореня x. Блок-схема алгоритму представлена на Рис. 5.

Геометрична інтерпретація методу ітерацій

При 0 < │f(x )│< 1 {x_n} сходиться до x* з тієї сторони, з якою розташовано початкове наближення малюнок 3, а та б.

При -1 < │f(x )│< 1 послідовні наближення {x_n} по черзі розташовані з різних сторін від рішення x*, малюнок 4, а та б.

При │f(x )│> 1 {x_n} не сходиться до x*, тому треба скористатися іншим чисельним методом рішення нелінійного рівняння F(x)=0.

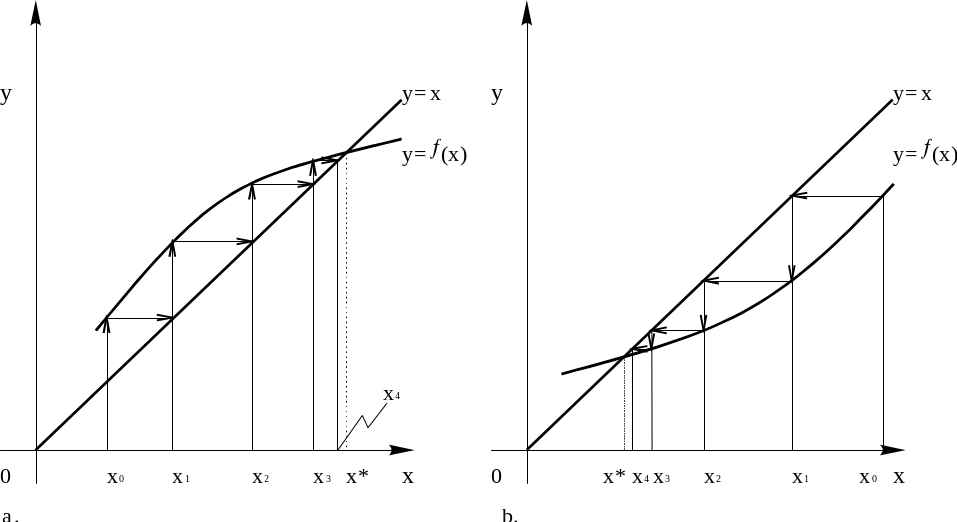x* – рішення нелінійного рівняння ;

х0 – початкове наближення.

Рис. 3.

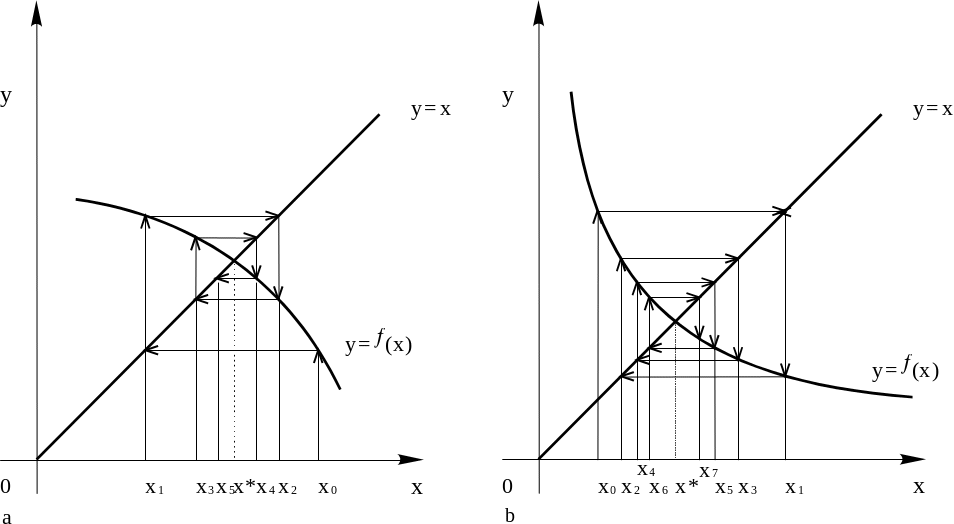Рис. 4.

Вибір початкового наближення : значення X = А або X = B, або X= ( A+B) /2 може бути вибрано як початкове наближення.

Рис. 5.

Приклад 1 : x2-ln(x) -2=0 ;

F(x)= x2 - ln(x) -2 x = ;

f(x) =

2.2. Метод Ньютона (метод дотичних)

Теорема. Хай функція F(x) при а ≤x ≤ b визначена і безперервна. Хай є два числа x1 і x2 : а ≤ x1 < x2 ≤ b. Якщо F(x1) і F(x2) мають протилежні знаки, то між x1 і x2 існує хоча б один корінь рівняння F(x)=0. (рис. 6.)

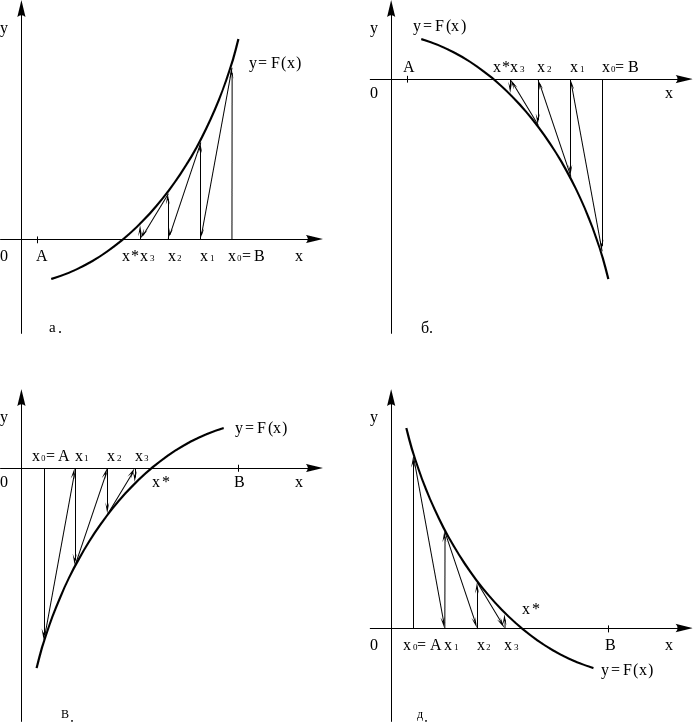
Рис.6

Ї

Рівняння дотичної, проведеної до кривої у = F(x) в крапці x0 : у = F(x0)+ (x-x0) F’(x0); , де x1 – точка перетину дотичної з віссю абсцис. Елементи послідовності {xn} обчислюються по наступному рекурентному співвідношенню до тих пір, поки виконується умова | xn+1- xn| ε де ε – задана погрішність обчислення кореня x.

Як х₀ вибирається той кінець відрізка [ а ; b ], на якому знаки F(x₀) і F"(x₀) співпадають. Блок-схема алгоритму представлена на рис.7.

Р ис. 7

2.3. Метод дихотомії

Дано : F(x)=0, x0  а ; b

Знайти : корінь нелінійного рівняння з точністю ε. Елементи послідовності {xn} обчислюються по формулі x = ( А + B )/2, а черговий інтервал вибирається з умови :

якщо F(x)* F(А)< 0, то В = х, інакше А = х, рис. 8, а, б. Елементи послідовності {xn} обчислюються до тих пір, поки виконується умова | B -A | > εде ε точність знаходження кореня рівняння F(x)=0.

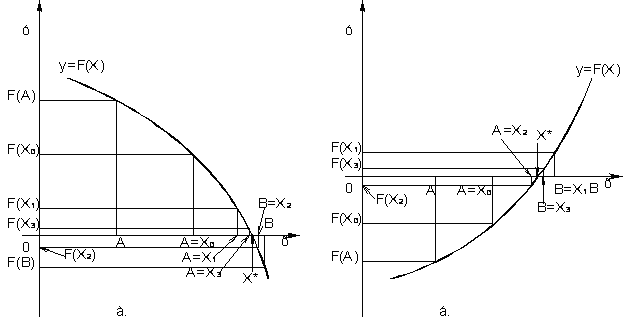
Рис. 8

HI

A=X

B=X

N=N-1

X=(A+B)/2

||B-A|<E

N=N+1

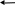
Рис. 9

2.4. Метод хорд

В цьому методі кожне значення x_n+1 знаходиться як точка перетину осі абсцис з хордою, проведеною через крапки з координатами (F(А),A) і (F(B),B), причому з цих крапок фіксується та, для якої знаки F(x) і F"(x) однакові. Якщо нерухомий кінець хорди x = А, то

,

початкове наближення x0 = В . Якщо нерухомий кінець хорди х = В, то

,

початкове наближення x0=А, малюнок 10, а - г. Обчислення проводяться до тих пір, поки | xn+1 - xn | ≥ ε , де ε – точність обчислення кореня рівняння F(x)= 0.

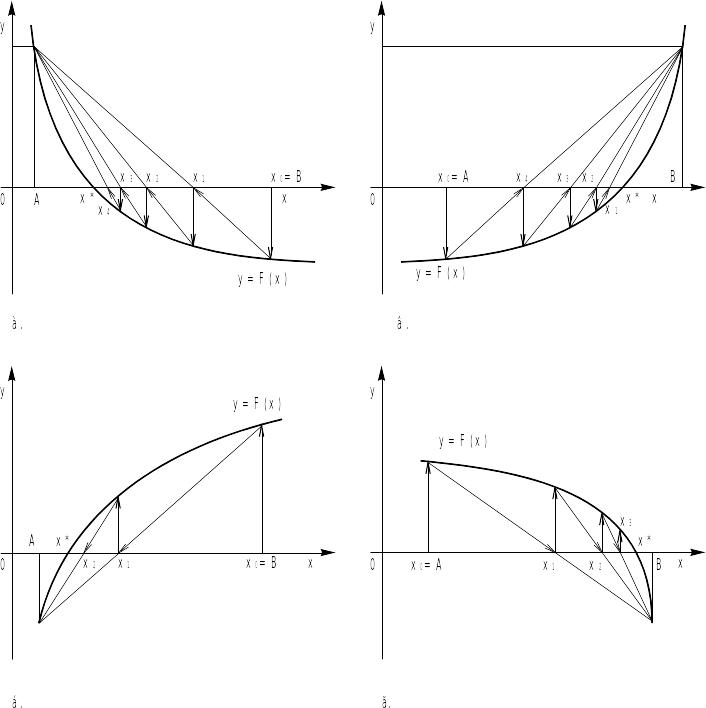
Рис.. 10.

Блок-схема алгоритму представлена на рис 11.

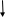
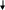
N=N+1

Рис. 11