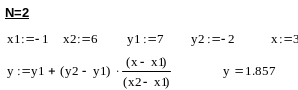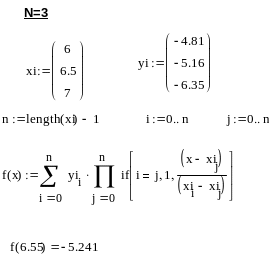3.3. Хибність інтерполяції

Якщо функція f(x), яка підлягає інтерполяції, достатнє число разів диференцюєма, то можна вивести формулу для визначення хибності інтерполяції. Оцінка максимальної хибності інтерполяції на всьому відрізку [ а ; b ] :

Mn

max | (x) - F_n-1(x)|  max | W_n-1(x)| ;

[а,b] n!

Mn = max | ⁽ⁿ⁾(x) | <  ;

[а,b]

W_n-1(x)= (x-x₁)(x-x₂)...(x-x_n-1).

3.4. Багатоінтервальна інтерполяція

Багатоінтервальна інтерполяція полягає в інтерполяції у(x) у ряді часткових інтервалів (які обмежені двома вузлами або групою вузлів) окремими поліномами невисокого ступеня. Така інтерполяція може застосовуватися при широкому загальному відрізку [а ; b], коли звичайна інтерполяція поліномом високого ступеня дає велику погрішність і веде до більшого часу обчислень. Помітимо також, що по вигляду полінома і значенням його коєфіціентів важко судити про вид залежності у(x).

Сплайн - інтерполяця

Сплайн-інтерполяція – є спеціальний вид багатоінтервальної інтерполяції.

Визначення. Хай відрізок [ а ; b ] розбитий на ( N-1 ) рівних часткових відрізків [ x_i, x_i+1 ],

де x_i = а + ( i-1 ) h, i = 1, 2,..., N-1, x_N = b ; x₁ = а ;

h = ( b - а ) / ( N-1 ).

Сплайном назвається функція, яка разом з декількома похідними безперервна на всьому заданому відрізку [ x_i ; x_i+1 ] окремо є деяким многочленом алгебри.

Максимальний по всіх часткових відрізках ступінь многочленів називається ступенем сплайна, а різниця між ступенем сплайна і порядком щонайвищої безперервної на [ а, b ] похідній – дефектом сплайна

Наприклад, безперервна шматково – лінійна функція ( рис. 19 ) ( ламана ) є сплайном першому ступеню з дефектом, рівному одиниці, оскільки безперервна тільки сама функція ( нульова похідна ), а перша похідна вже розривна.

На практиці найширше вживання одержали сплайны третьому ступеню, мають на [ а, b ] безперервну, принаймні, першу похідну.

Ці сплайны називаються кубічними і позначаються через S₃(x). Величина mi = S′₃(xi) називається нахилом сплайна в точці ( вузлі ) xi. В загальному випадку сплайн задається глобальним способом, тобто з використанням всіх вузлів при будь-якому їх розташуванні. Розглянемо кубічний сплайн, заданий локальним способом. Це завдання реалізується порівняно просто і потрибує істотно меншого об'єму пам'яті ЕОМ, ніж при глобальному способі завдання.

Кубічний сплайн, заданий локально – це інтерполююча функція у вигляді полінома третього ступеня, обчислювана по формулах :

i = int (( b-a ) / h ) ;

h = ( b-a ) / ( N-1) ;

(x_i+1-x)²(2(x-x_i)+h) (x-xi) ²(2(x_i+1-x)+h)

S3(x)= ----------------------- yi + ----------------------- y_i+1 +

h³ h³

(x_i+1-x)2(x-x_i) (x-x_i) 2(x-x_i+1)

+ ----------------- mi - ---------------- m_i+1

h² h²

де m_i, m_i+1 – перші похідні S₃(x).

Похідні локального сплайна можуть задаватися двома способами.

Спосіб 1. Похідні m_i і m_i+1 обчислюються за допомогою формул чисельного диференціювання по трьох крапках:

m_i=(y_i+1-yi-1)/2h , i=2, ..., n-1 ;

m_i=(4y₂-y₃-3y₁)/2h , i=1 ;

mn=(3y_n+y_n-2-4y_n-1)/2h , i=n .

Спосіб зручний тим, що для завдання сплайна вимагається вводити лише ординати yi (значення mi обчислюються програмою). Для зменшення часу багатократних обчислень у(x) бажано заздалегідь обчислити масив mi і берегти його в пам'яті ЕОМ.

Спосіб 2. Значення mi (обчислені окремо або одержані з графіка як нахили його у вузлах) задаються безпосередньо у вигляді масиву mi.

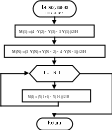
Блок-схема алгоритму представлена на рис. 20.

Примітка. Видачу результату здійснити з відповідними коментарями.

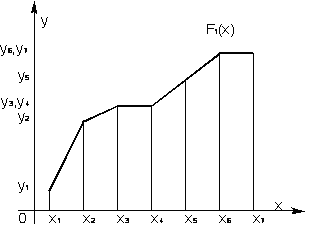
Рис. 19

Рис. 20

Форма Лагранжа	Форма Лагранжа

ЛІТЕРАТУРА

1. Бронштейн И.Н., Семендяев К.А. Довідник по математиці. – М.: Наука, 1986. – 544 с.

2. Волков Е.А. Чисельні методи: Навчальний посібник для вузів. –.: Наука, 1987. – 248 с.

3. Дьяконов В.П., І.В. Абраменкова MathCad 8 PRO в математиці, фізиці та Internet. – М.: „Нолидж”, 1999., 512 с., іл..

4. Дьяконов В.П. Довідник по алгоритмах і програмах на мові Бейсік для ПЕОМ. – М.: „Наука”, 1987. – 240 с.

5. Кир’янов Д.В. MathCad 12. – СПб.: БХВ-Петербург, 2005. – 576 с.: іл..

6. Сергованцев В.Т., Смирнов С.М. Збірка задач по обчислювальній техніці в інженерних і економічних розрахунках. – М.: ”Фінанси і статистика”, 1985. – 160 с.

7. Черняк А.А., Новиков В.А., Мельников О.І., Кузнєцов А.В. Математика для економістів на базі MathCad. – СПб.: БХВ–Петербург, 2003. – 496 с.: іл..

Навчальне видання