3.1. Форма Лагранжа

Інтерполяційний багаточлен Лагранжа, побудований по таблиці

(x1, y1); (x2, y2);

(x3, y3);…, (xn, yn), має вигляд

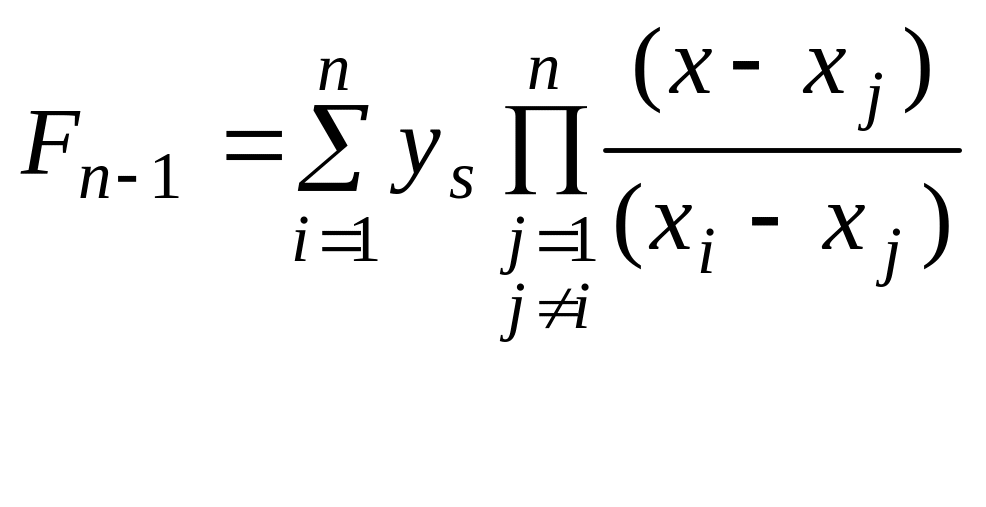. (1)

3.1.1 Лінійна інтерполяція

Хай задана таблиця x₁, x₂, …, x_n 

y₁, y₂, …, y_n , xi – різні.

Необхідно обчислити у в крапці x:

x_i1, x_i2 – найближчі до х вузли з набору x₁, x₂, …, x_n. Лінійна інтерполяція здійснюється по двох найближчих крапках.

Приклад 1

a). х [ x₁, x₂ ].

Тоді x_i1 = x₁ ; y_i1 = y₁,

x_i2 = x₂ ; y_i2 = y₂,

b). х [ x₄, x₅ ]

x_i1 = x₄ ; y_i1 = y₄,

x_i2 = x₅ ; y_i2 = y₅ , (рис. 12).

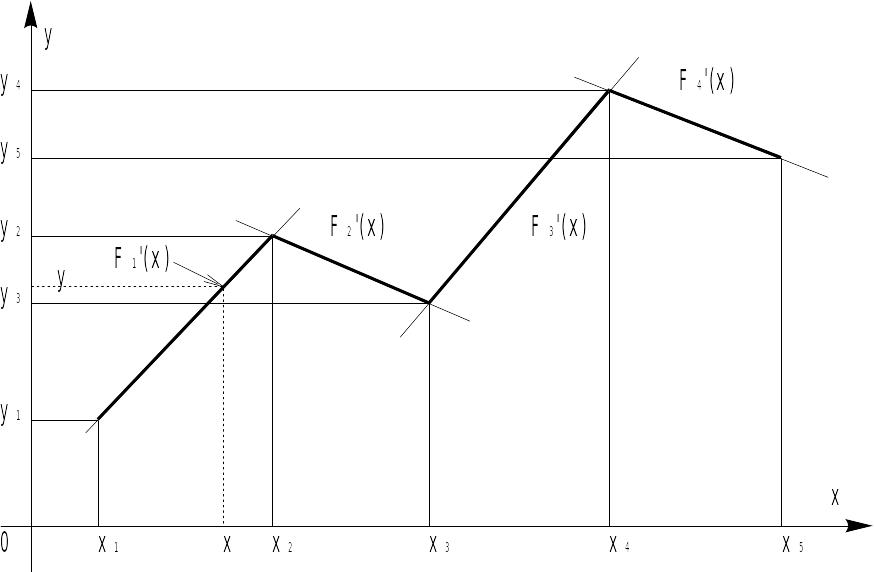
Рис. 12

На рис.13 представлена блок-схема алгоритму розрахунку інтерполяційного значення функції в крапці x по двох найближчих вузлових крапках, координати яких є початковими даними.

Основні позначення :

x₀ – значення х, при якому обчислюється інтерполяційне значення у ;

у₀ – інтерполяційне значення в крапці х0 ;

L – код помилки ;

x(1), x(2) – табличні значення аргументів ;

у(1), у(2) – табличні значення функції.

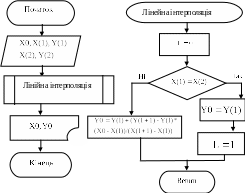
Рис. 13

На малюнку 14 представлена блок-схема алгоритму розрахунку інтерполяційного значення функції в будь-якій точці х з вибором найближчих вузлових крапок, по яким буде проводитися інтерполяція. Початковими даними є координати всіх експериментальних крапок і значення х, для якого потрібно обчислити інтерполяційне значення функції.

3.1.2. Квадратична інтерполяція

де x_i1, x_i2, x_i3 – найближчі до х вузлові крапки (рис. 15 ).

Квадратична інтерполяція здійснюється по трьох найближчих крапках.

Приклад 2

а). х  [ x₁, x₃ ]

б). х  [ x₃, x₅ ]

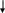
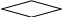
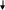
Рис.14.

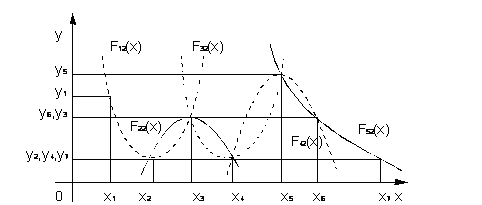
Рис.15.

3.1.3. Інтерполяція багаточленом степені n-1

Інтерполяцію багаточленом степені (n-1) виконують по n експериментальних крапках (малюнок 16). Інтерполяція здійснюватиметься по формулі (1). Блок-схема алгоритму представлена на малюнку 17.

Основні позначення:

Х і У – масиви розмірністю N;

N – число вузлових крапок;

x₀ – значення х, при якому необхідно знайти інтерпольоване значення функції;

у₀ – значення функції, обчислене в крапці x₀.

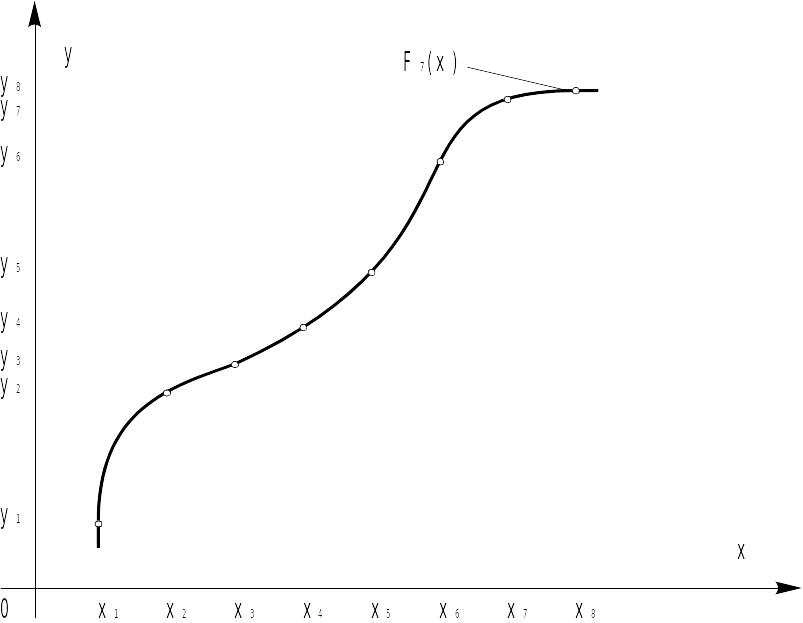
Рис. 16

3. 2. Форма Ньютона

Визначення. Хай x₁, x₂, …, x_n – довільні крапки (вузли), причому x_i x_j при i  j. Значення y₁, y_{2 ...,} y_n функції у в вузлах називаються розділеними різницями нульового порядку і позначаються як [xi], де i=1,….N.

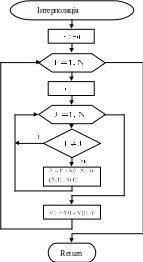
Рис.17

[ x₁] = y₁

[ x₂] = y₂

. . .

[ x_n] = y_n [ x_i] = y_i i = 1,… n .

Число у( x₁; x₂)= у( x₂; x₁)=

називається розподіленою різницею першого порядку функції у і позначається [x₁;x₂] = [x₂;x₁].

В загальному вигляді

у( x_i-1; x_i)= у( x_i; x_i-1)= де i =1,… n

Число

називаються розділеною різницею другого порядку функції у і позначаються [ x₁ ; x₂ ; x₃ ] .

В загальному вигляді

де i =1,… n

Розділена різниця k-го порядку визначається через розділені різниці ( k-1) -го порядку по рекурентній формулі , k =1,… n-1; aбо .

Наприклад, k= 1

Лема. Хай x1, x2 ., xn довільні попарно неспівпадаючі вузли, в яких відомі значення функції y1, y2, yn. Алгебраїчний багаточлен ( n - 1) степені

L_n-1(x)= у(x₁)+(x-x₁₎ у(x_1,x₂)+ (x-x₁)₍x-x₂)у₍x₁,x₂,x₃)+ (x-x₁)(x-x₂)…(x-x_n-1) у(x_1,x_2,x_3,…x_n) (2)

є інтерполяційним, тобто L_n-1(x_i)= у(x_i), i = 1, n.

Оскільки розділені різниці у(x₁), у(x₁; x₂), …, у( x₁; x₂; …x_n) це цілком певні числа то функція (2) є багаточленом (n-1)-й степені. Багаточлен (2) називається інтерполяційним багаточленом Ньютона для нерівних проміжків. Згідно твердженню, існує тільки один інтерполяційний багаточлен. Інтерполяційний багаточлен Лагранжа тотожно співпадає з інтерполяційним багаточленом Ньютона, тобто L_n-1(x)= F_n-1(x)

У інтерполяційного багаточлена Лагранжа бачимо наочну його залежність від кожного значення функції y_i, де i = 1, n. Це у багатьох випадках корисно. Проте при зміні n інтерполяційний багаточлен Лагранжа треба будувати наново. В цьому полягає його недолік.

Інтерполяційний багаточлен Ньютона (2) виражається не через значення функції у, а через її розділені різниці. При зміні степеня n у інтерполяційного багаточлена Ньютона потрібно додати або відкинути відповідне число стандартних доданків, Це зручно на практиці і прискорює процес обчислень. Інтерполяційний багаточлен Ньютона можна записати у вигляді

де i=2,…n

i=2,…n

При обчисленнях розділені різниці записуються у вигляді таблиці 4

Таблиця 4.1

xi	[xi]	[xi xi+1]	[xi;xi+1;xi+2]	[xi;xi+1;xi+2;xi+3]	[xi;xi+1;xi+2;xi+3;xi+4]
x1	у(x1)
		у(x1;x2)
x2	у(x2)		у(x1;x2;x3)
		у(x2;x3)		у(x1;x2;x3;x4)
x3	у(x3)		у(x2;x3;x4)		у(x1;x2;x3;x4;x5)
		у(x3;x4)		у(x2;x3;x4;x5)
x4	у(x4)		у(x3;x4;x5)
		у(x4;x5)
x5	у(x5)

Програма використовує наступні змінні :

Х0 – аргумент, при якому необхідно обчислити значення функції ;

(N-1) – ступінь багаточлена ;

N – число експериментальних даних ;

X(N),Y(N) – масиви, i = 1,N:

I,K – параметри циклів ;

L – значення багаточленів в крапці Х0 ;

P і I1 – робочі змінні.

Зауваження: розділені різниці заносяться в масив У. Блок-схема алгоритму представлена на рис. 18

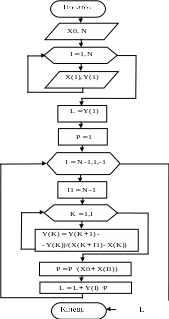
Рис.18