Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный горный институт имени Г.В.Плеханова

(технический университет)

Высшая математика

Ряды. Функции нескольких переменных.

Теория вероятностей и элементы

математической статистики

Учебно-методическое пособие

Санкт-Петербург

2009

УДК 517.52 (075.80)

ББК 22.161.1 + 22.161.6 + 22.131

        В723

Авторы:

А.П.Господариков, Т.Р.Акчурин, И.А.Лебедев, В.В.Тарабан

Учебно-методическое пособие дает возможность получить практические навыки при самостоятельном изучении материала и выполнении контрольных работ по темам, входящим в программу второго курса высшей математики.

Предназначено для студентов заочной формы обучения технических специальностей.

Научный редактор проф. А.П.Господариков

Рецензенты: кафедра прикладной математики (Санкт-Петербургский государственный университет путей сообщения); д-р физ.-мат. наук проф. С.И.Перегудин (Санкт-Петербургский государственный университет).

В723	Высшая математика. Ряды. Функции нескольких переменных. Теория вероятностей и элементы математической статистики: Учебно-методическое пособие / А.П.Господариков, Т.Р.Акчурин, И.А.Лебедев, В.В.Тарабан; Санкт-Петербургский государственный горный институт (технический университет). СПб, 2009. 113 с.

ISBN 978-5-94211-382-7

УДК 517.52 (075.80)

ББК 22.161.1 + 22.161.6 + 22.131

ISBN 978-5-94211-382-7

Ó Санкт-Петербургский горный институт имени Г.В.Плеханова, 2009

Введение

Изучая разделы курса высшей математики, необходимо научиться исследовать сходимость рядов, использовать функциональные ряды для вычислений и решения дифференциальных уравнений, находить и использовать частные производные функций нескольких переменных, вычислять кратные и криволинейные интегралы, а также применять теорию вероятностей и обрабатывать статистический материал.

Программа

1. Числовые ряды. Признаки сходимости числовых рядов.

2. Степенные ряды. Разложение функций в степенные ряды.

3. Применение степенных рядов для приближенных вычислений.

4. Ряды Фурье и их применение (метод Фурье).

5. Частные производные и полный дифференциал функций нескольких переменных.

6. Касательная плоскость и нормаль к поверхности.

7. Частные производные высших порядков функций нескольких переменных.

8. Градиент и производная по направлению.

9. Экстремум функции нескольких переменных.

10. Наибольшее и наименьшее значения функций нескольких переменных.

11. Двойной интеграл. Вычисление двойного интеграла.

12. Двойной интеграл в полярных координатах.

13. Тройной интеграл. Вычисление тройного интеграла.

14. Тройной интеграл в цилиндрических и сферических координатах.

15. Приложения кратных интегралов (вычисление объема, массы, центра тяжести, моментов инерции).

16. Криволинейные интегралы первого и второго рода. Формула Грина.

17. Независимость криволинейного интеграла второго рода от пути интегрирования.

18. Случайные события. Основные понятия теории вероятностей.

19. Вероятность суммы событий.

20. Вероятность произведения событий.

21. Формула полной вероятности и формула Байеса.

22. Повторение независимых опытов и теоремы Лапласа.

23. Теорема Бернулли и закон Пуассона.

24. Случайные величины. Закон распределения и функция распределения.

25. Математическое ожидание случайной величины.

26. Дисперсия и среднее отклонение случайной величины.

27. Биномиальный закон распределения и закон Пуассона.

28. Равномерный и нормальный законы распределения.

29. Система двух случайных величин. Закон и функция распределения.

30. Условный закон распределения и условное математическое ожидание.

31. Начальные и центральные моменты случайной величины и системы случайных величин. Коэффициент корреляции.

32. Выборка и эмпирическое распределение. Графическое представление.

33. Точечные оценки параметров распределения по эмпирическим данным.

34. Интервальные оценки параметров распределения по эмпирическим данным.

35. Понятие о критерии согласия. Критерий Пирсона хи-квадрат.

36. Статистическая и корреляционная связь. Уравнения прямых регрессий.

37^. Векторное поле. Циркуляция, поток, дивергенция и ротор.

38. Формула Стокса и формула Остроградского. Потенциальные и соленоидальные векторные поля.

39. Операционное исчисление. Теоремы об оригиналах и изображениях.

40. Применение операционного исчисления к решению дифференциальных уравнений.

1. Ряды

1.1. Сходимость числовых рядов

Рядом называется выражение вида

.

Ряд сходится, если существует конечный предел частичных сумм, образованных первыми членами ряда:

где

Этот предел называется суммой ряда.

Если конечного предела нет, то ряд расходится. Сумму сходящегося ряда можно найти приближенно, заменяя ее на частичную сумму с достаточно большим номером: . При этом остаток ряда

позволяет оценить точность такого приближения; при .

Сходимость и расходимость ряда не зависит от конечного числа членов.

Необходимый признак сходимости. Если ряд сходится, то . Следовательно, если , то ряд расходится (достаточный признак расходимости). Заметим, что необходимое условие не является достаточным для сходимости: так, для расходящегося гармонического ряда имеем .

Для положительных рядов ( ) имеются четыре основных признака сходимости.

Признак сравнения. 1. Пусть (n = 1, 2, …). Если ряд сходится, то сходится и ряд ; если ряд расходится, то расходится и ряд . 2. Ряды и сходятся и расходятся одновременно, если .

Последний предельный признак сравнения удобно применять к рядам, общий член которых зависит только от степеней переменной n. В этом случае ряд сравниваем с рядом Дирихле , который сходится при p > 1 и расходится при p  1.

Признак Даламбера. Если , то при ряд сходится, а при ряд расходится.

Этот признак удобно применять к рядам, общий член которых зависит от степеней и показательных функций переменной n, или содержит факториалы. Напомним определение факториала:

0! = 1, 1! = 1, 2! = 12, 3! = 123 = 6, …, n! = 12 …  (n – 1)n.

Радикальный признак Коши. Если , то при ряд сходится, а при – расходится.

Этот признак удобно применять к рядам, общий член которых зависит только от показательных функций переменной n.

Замечание. Признаки Даламбера и Коши (радикальный) не позволяют судить о сходимости ряда в случае l = 1 (требуется дополнительное исследование сходимости ряда или применение другого достаточного признака).

Интегральный признак Коши. Если непрерывная функция f(x) монотонно убывает на [1,) и a_n = f(n), то ряд и интеграл сходятся или расходятся одновременно.

Этот признак удобно применять к ряду, для которого нетрудно проинтегрировать функцию, задающую общий член ряда.

Пример 1. Определить сходимость или расходимость рядов:

1.  . 2.  . 3.  . 4.  . 5.  .  6.  .

Решение.

1.  , т.е. ряд расходится (признак расходимости).

2. Так как общий член ряда зависит только от степеней n , то для применения признака сравнения надо определить, какой степени n эквивалентно это выражение при n  :

.

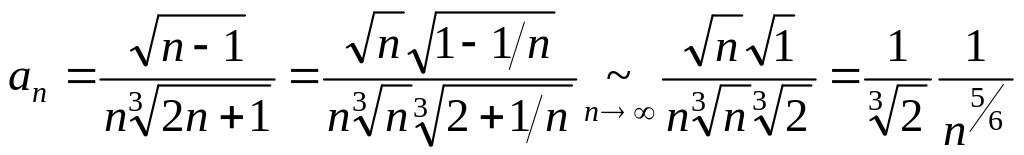Если 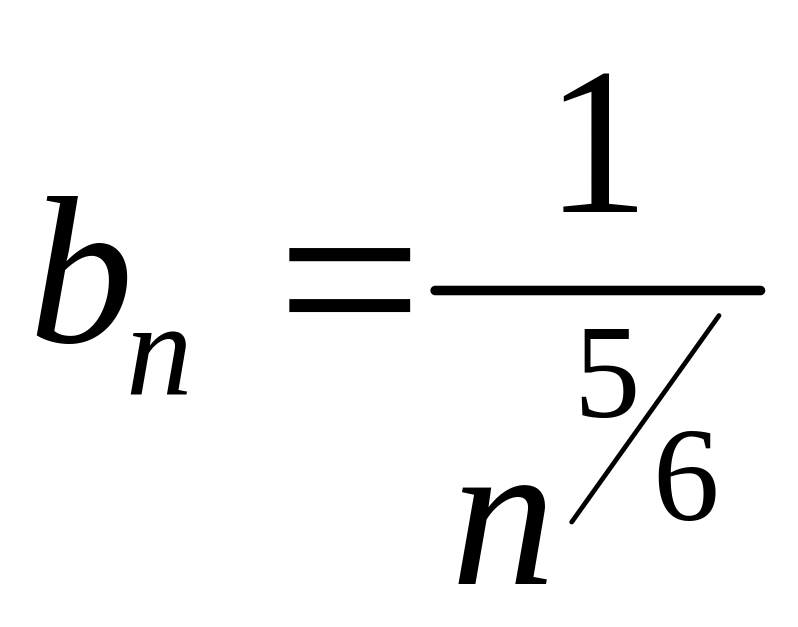, то в силу этой эквивалентности имеем

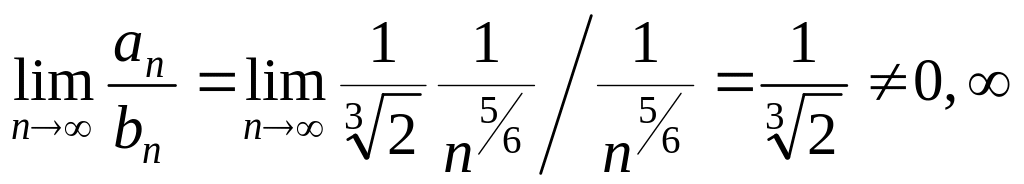
и по предельному признаку сравнения ряд расходится, так как расходится ряд Дирихле с показателем p = 5/6 < 1.

3.  . Найдем ,

и по признаку Даламбера ряд сходится.

4.  ,

= 

и по признаку Даламбера ряд сходится.

5.  . Найдем

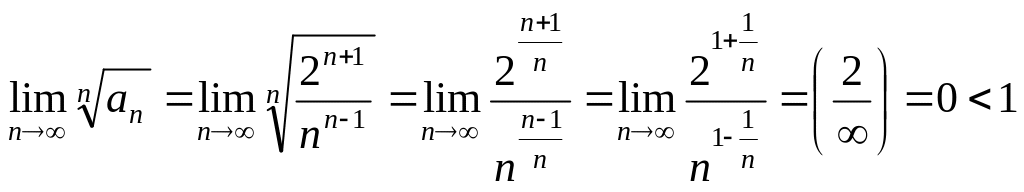
и по радикальному признаку ряд сходится.

6.  – непрерывная функция, убывающая на промежутке ; несобственный интеграл

сходится, и поэтому по интегральному признаку ряд тоже сходится.

Если для ряда с членами а_n произвольного знака сходится положительный ряд , из абсолютных величин его членов, то ряд называется абсолютно сходящимся. Если ряд сходится, а ряд расходится, то ряд называется условно сходящимся.

Для знакочередующихся рядов , где имеется следующий признак сходимости:

Признак Лейбница. Если для знакочередующегося ряда выполнено условие и члены монотонно убывают , то ряд сходится.

Следствие.

Пример 2. Определить сходимость рядов:

1.  . 2.  .

Решение. 1. Рассмотрим

,

где ряд из абсолютных величин сравним с рядом Дирихле , который сходится (p = 2 > 1). Тогда по предельному признаку сравнения ряд сходится абсолютно.

2. ,

т.е. такой ряд сравним с гармоническим, который расходится. По предельному признаку сравнения ряд из абсолютных величин также расходится, т.е. исходный ряд абсолютно расходится. Проверим для данного знакочередующегося ряда условия признака Лейбница:

,

члены монотонно убывают и, следовательно, по признаку Лейбница данный ряд сходится условно.