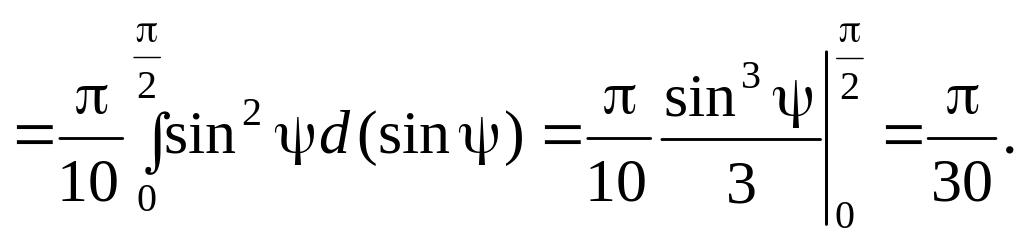- •Введение
- •Программа
- •1. Ряды
- •1.1. Сходимость числовых рядов
- •1.2. Степенные ряды. Разложение функций в степенные ряды
- •1.3. Применение степенных рядов
- •1.4. Ряды Фурье и их применение
- •2. Дифференциальное исчисление функций нескольких переменных
- •2.1. Частные производные и дифференциалы функций нескольких переменных
- •2.2. Экстремум функций нескольких переменных
- •2.3. Оптимизация функций нескольких переменных
- •3. Интегральное исчисление функций нескольких переменных
- •3.1. Двойной интеграл. Замена переменных
- •3.2. Вычисление объемов тел с помощью двойного интеграла
- •3.3. Вычисление тройного интеграла в декартовых координатах
- •3.4. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.5. Криволинейный интеграл первого рода
- •3.6. Криволинейный интеграл второго рода
- •3.7. Теорема Грина и независимость криволинейного интеграла от пути интегрирования
- •4. Элементы теории поля
- •4.1. Операционное исчисление и его применение
- •Контрольная работа 6
- •Контрольная работа 7
- •Контрольная работа 8
- •5. Теория вероятностей
- •5.1. Основные понятия теории вероятностей
- •5.2. Повторение независимых опытов
- •5.3. Случайные величины и их числовые характеристики
- •5.4. Система двух случайных величин и регрессия
- •6. Основы математической статистики
- •Контрольная работа 9
- •Контрольная работа 10
- •Рекомендательный библиографический список
- •Оглавление
3.2. Вычисление объемов тел с помощью двойного интеграла
Если тело V ограничено сверху
непрерывной поверхностью
![]() ,
снизу поверхностью
,
снизу поверхностью
![]() ,
а боковой поверхностью является
цилиндрическая поверхность с образующей,
параллельной оси Oz (проекцией тела
V на плоскость
,
а боковой поверхностью является
цилиндрическая поверхность с образующей,
параллельной оси Oz (проекцией тела
V на плоскость
![]() является область
),
то объем этого тела вычисляется по
формуле
является область
),
то объем этого тела вычисляется по
формуле
![]() .
(19)
.
(19)
Пример 16. Вычислить объем тела,
ограниченного поверхностями
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис.7).
(рис.7).
Решение. Плоскости
и
являются боковыми границами тела, так
как в их уравнениях нет переменной z.
Область интегрирования
ограничена линиями (следами боковых
границ) c такими же уравнениями как у
боковых стенок
и
и проекцией на Oxy линии пересечения
поверхностей
и
.
Исключая из этих уравнений z,
получим линии пересечения:
![]()
![]() (рис.8).
(рис.8).


![]() находим
находим
![]() .
Для поверхности
.
Для поверхности
![]() находим
находим
![]() = –1. Так как
= –1. Так как
![]() ,
то
– крышка и
,
то
– крышка и
![]() – дно. По формуле (19), рассматривая
область S как область
I типа и расставляя
пределы интегрирования, получим объем
тела
– дно. По формуле (19), рассматривая
область S как область
I типа и расставляя
пределы интегрирования, получим объем
тела
![]()
![]()
3.3. Вычисление тройного интеграла в декартовых координатах
Тройной интеграл определяется аналогично
двойному интегралу как предел
соответствующих интегральных сумм для
функции трех переменных. Условия
существования и свойства тройного
интеграла такие же, как у двойного
интеграла. Вычисление тройного интеграла
сводится к последовательному вычислению
трех определенных интегралов. Предположим,
что областью интегрирования является
тело
![]() ,
ограниченное снизу поверхностью
,
ограниченное снизу поверхностью
![]() ,
а сверху – поверхностью
,
а сверху – поверхностью
![]() .
Пусть это тело проектируется на область
D плоскости
,
элементарный объем
.
Пусть это тело проектируется на область
D плоскости
,
элементарный объем
![]() .
Тройной интеграл сводится к двойному
интегралу по области проекции D и
интегралу по dz.
.
Тройной интеграл сводится к двойному
интегралу по области проекции D и
интегралу по dz.
Если функция
![]() непрерывна в области
,
то
непрерывна в области
,
то

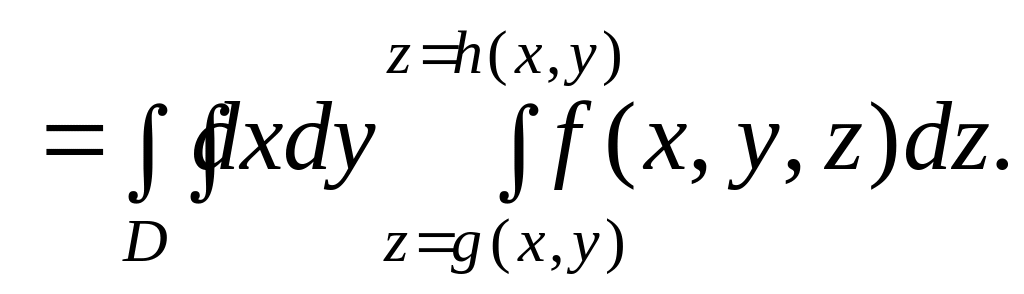
В частности, объем
![]() .
.

![]() ,
если областью интегрирования служит
пирамида, ограниченная плоскостями
,
если областью интегрирования служит
пирамида, ограниченная плоскостями
![]() ,
,
![]() ,
,
![]() и
и
![]() (рис.9).
(рис.9).
Решение. Область
![]() ,
на которую проектируется пирамида, есть
треугольник на плоскости
,
ограниченный прямыми
,
,
.
Так как на нижней поверхности
,
а на верхней
,
на которую проектируется пирамида, есть
треугольник на плоскости
,
ограниченный прямыми
,
,
.
Так как на нижней поверхности
,
а на верхней
![]() ,
то
,
то
![]() .
.
Вычисляя последовательно, получим
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
3.4. Вычисление тройного интеграла в цилиндрических и сферических координатах
Наряду с декартовыми координатами при вычислении тройного интеграла часто используется цилиндрическая система координат. Цилиндрические координаты связаны с декартовыми следующими соотношениями:
![]() ,
,
![]() ,
,
![]() .
.
Тогда замена координат имеет вид
![]() ,
(20)
,
(20)
где
![]() – область интегрирования в новых
координатах и якобиан
.
– область интегрирования в новых
координатах и якобиан
.
Пример 18. Определить массу
![]() прямого кругового цилиндра V
с высотой h и радиусом
основания R, если
плотность в любой
точке цилиндра равна расстоянию от этой
точки до оси цилиндра = r.
прямого кругового цилиндра V
с высотой h и радиусом
основания R, если
плотность в любой
точке цилиндра равна расстоянию от этой
точки до оси цилиндра = r.
Решение. Введем цилиндрическую систему координат, направив ось аппликат по оси цилиндра и совместив плоскость с нижним основанием цилиндра. Масса цилиндра равна тройному интегралу от плотности и по формуле (20)
![]() .
.
Пусть теперь в
пространстве задано тело
,
плотность которого в любой точке есть
функция координат этой точки:
![]() .
Координаты
центра тяжести этого тела находятся по
формулам
.
Координаты
центра тяжести этого тела находятся по
формулам
 ;
;
 ;
;
 .
(21)
.
(21)
Момент инерции
![]() тела
относительно оси
тела
относительно оси
![]()
![]() .
.
Аналогичные формулы имеют место для
моментов инерции
![]() и
и
![]() относительно осей
относительно осей
![]() и
и
![]() соответственно:
соответственно:
![]() ;
;
![]() .
(22)
.
(22)
Для плоских областей справедливы такие же формулы, как (21) и (17), но вместо тройного интеграла используется двойной.
Пример 19. Найти абсциссу
![]() центра тяжести тела
из примера 16. Тело считать однородным
с плотностью
центра тяжести тела
из примера 16. Тело считать однородным
с плотностью![]() .
.
Решение. Так как
![]() ,
то по (21) имеем
,
то по (21) имеем
![]()

![]() .
.
Пример 20. Найти момент инерции
тела относительно оси Oz,
ограниченного поверхностями
![]() и
и
![]() (рис.10). Плотность = 1.
(рис.10). Плотность = 1.
Решение. Найдем проекцию на
плоскость xOy линии
пересечения поверхностей z = 1 + x2 + y2
и z = 3:
1 + x2 + y2 = 3,
откуда x2 + y2 = 2.
Это окружность радиусом
![]() с центром в начале координат.
Воспользовавшись формулой (20), перейдем
к цилиндрическим координатам:
с центром в начале координат.
Воспользовавшись формулой (20), перейдем
к цилиндрическим координатам:

![]() .
.

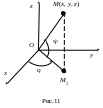
![]() ,
отсчитываемым от плоскости xOy,
полярным (или меридиональным) углом
проекции М1 точки М на
плоскость xOy и сферическим радиусом ,
равным расстоянию от точки до полюса O
(начала координат), т.е. = ОМ.
Формулы перехода от декартовой
прямоугольной к сферической системе
координат имеют вид
,
отсчитываемым от плоскости xOy,
полярным (или меридиональным) углом
проекции М1 точки М на
плоскость xOy и сферическим радиусом ,
равным расстоянию от точки до полюса O
(начала координат), т.е. = ОМ.
Формулы перехода от декартовой
прямоугольной к сферической системе
координат имеют вид
![]()
В этом случае якобиан
![]() и
и
![]()
![]() .
(23)
.
(23)
Пример 21. Найти
![]() по области V, ограниченной сферой
по области V, ограниченной сферой
![]() и плоскостями
и плоскостями
![]() (I октант).
(I октант).
![]()