Лабораторна робота №3 Моделювання динаміки пружної системи верстата

Мета роботи: визначення динамічних характеристик пружної системи верстата по методу механічних ланцюгів, побудова частотних характеристик системи з використанням пакета Mathcad

КОРОТКІ ТЕОРЕТИЧНІ ДАНІ

Динамічні характеристики систем з одним ступенем свободи

У

Рис. 1. Одномасова пружна система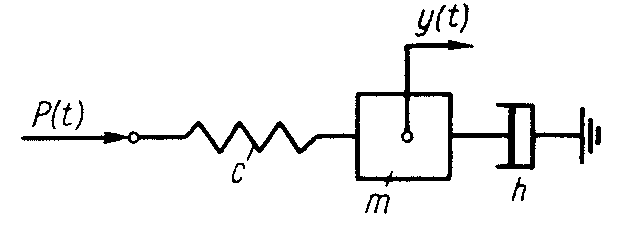

багатьох випадках пружні системи окремих елементів верстата можна приблизно привести до системи з одним ступенем свободи. Розглянемо таку найпростішу систему, що складається з маси т, пружної ланки з коефіцієнтом жорсткості з і демпфера в'язкого опору з коефіцієнтом демпфірування h (рис. 1). Вхідною координатою цієї системи є сила Р, що змінюється в часі і прикладена до вільного кінця пружної ланки, а вихідною координатою – переміщення у маси.

Рівняння руху системи

(3.1)

Перший член лівої частини рівняння (1) являє собою силу інерції, другий – силу демпфірування, третій – силу пружності.

Розділимо обидві частини рівняння на с і позначимо:

; ; ,

де – період власних коливань, с;

– власна кутова частота коливань, 1/с;

– власна частота коливань, Гц;

– постійна часу демпфірування, с;

– відносний коефіцієнт демпфірування;

– статична характеристика (податливість), мм/Н.

Рівняння (1) одержує наступний вигляд

(3.2)

Отже, динамічна характеристика пружної системи визначається трьома параметрами: К_ус, Т и ξ. Коефіцієнт ξ залежить від сил непружного опору, тому термін "пружна система" є певною мірою умовним.

Диференціальне рівняння (2) можна представити в більш компактній, операторній формі введенням символів операції диференціювання за часом

(3.3)

Операторна форма запису принципово не відрізняється від звичайної.

Передатна функція елемента чи системи є відношення вихідної координати х_вых до вхідного х_вх, записане в операторній формі:

.

Передатна функція може мати певну розмірність, що відповідає відношенню розмірності вихідної координати до вхідної, чи бути безрозмірною, коли координати виражені у відносних або однакових одиницях.

Стосовно до пружної системи передатна функція є відношення вихідної координати – пружного переміщення у – до вхідної координати – сили Р:

(3.4)

В усталеному русі (р = 0) передатна функція W переходить у статичну характеристику . У рівнянні (3.4) над позначеннями величин переміщення і сили, що змінюються в часі, додані хвилясті лінії, щоб підкреслити відмінність цих величин від величин, що входять у вираження для К_ус.

Перехідна, або часова, функція характеризує перехідний процес, що виникає після миттєвого прикладення до системи постійної сили Р, і визначається рішенням рівняння (3.3). Загальне вирішення цього рівняння виходить підсумовуванням рішення однорідного рівняння (без правої частини) і приватного рішення неоднорідного рівняння.

Якщо ξ > 1, то демпфірування велике і перехідний процес неколивальний, маса без коливань рухається до нового рівноважного стану. При східчастій зміні сили Р (рис. 3.2, а) графік перехідного процесу описується двома експонентами з різними постійними часу (рис. 3.2, б).

Якщо ξ < 1, те перехідний процес коливальний і графік його являє собою згасаючу синусоїду, амплітуда якої убуває по експонентному закону (рис. 3.2, в). Відношення будь-яких двох послідовних пікових значень одного знака залишається незмінним протягом усього процесу:

.

В

Рис. 3.2. Перехідні процеси одномасової системи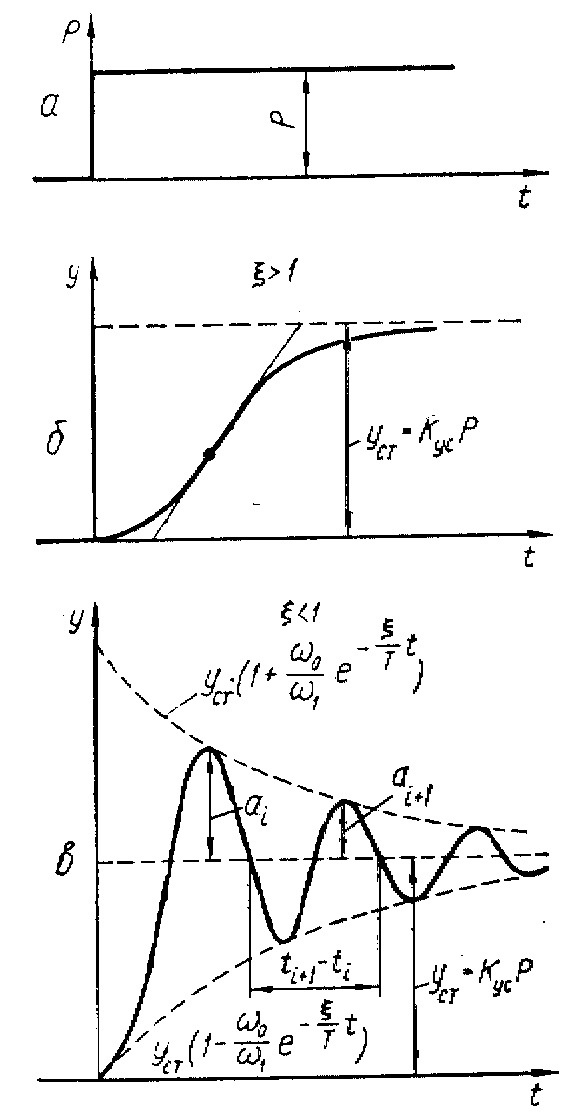

еличина характеризує ступінь затухання коливань і називається логарифмічним декрементом коливань.

Частотні характеристики описують сталі змушені коливання пружної системи, викликані гармонійним впливом на вході. Якщо до вільного кінця пружної ланки прикласти силу , то на виході системи після перехідного процесу установляться гармонійні коливання з амплітудою в₀ і тією же частотою, але зсунуті по фазі на кут φ.

Розглянуті функції можна представити на комплексній площині у вигляді обертових векторів Р₀ і у₀. Для кожного моменту часу сила визначається вектором Р₀ , проведеним з початку координат під кутом ωt до речовинної осі. Таким чином, речовинна частина гармонійної сили дорівнює , а уявна .

Позначивши комплексний вираз сили через Р(t), можна написати наступне рівняння:

,

де .

Оскільки по формулі Ейлера , то силу, що змінюється по гармонійному закону, можна виразити в комплексній показовій формі

.

Вираження можна розглядати як обертовий одиничний вектор, проекція якого на дійсну вісь дає гармонійний рух з одиничною амплітудою та з кутовою частотою ω.

Переміщення маси на виході пружної системи в комплексній показовій формі буде

.

Частотна характеристика пружної системи (або частотна передатна функція) є відношення вихідної координати (переміщення) до вхідної координати (сили)

,

де – відношення амплітуд вихідної і вхідної координат; – фазовий кут.

Оскільки ; , то оператору диференціювання відповідає і частотну передатну функцію системи можна одержати заміною перемінної на в рівнянні (3.4):

. (3.5)

Після перетворень рівняння (5) може бути представлене у вигляді

,

де – відповідно дійсна і уявна частини комплексного виразу.

Відношення амплітуд вихідної до вхідної координати (динамічна податливість)

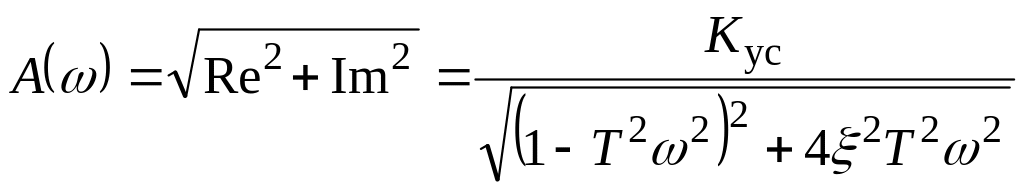, (3.6)

фазовий кут

(3.7)

Побудований на основі цих рівнянь графік залежності від відношення частот (амплітудно-частотна характеристика) показаний на рис. 3.3, а; графік залежності фазового кута φ від відношення частот (фазово-частотна характеристика) – на рис. 3.3, б, амплітудно-фазова частотна характеристика (АФЧХ) – на рис. 3.3, в. Вона побудована на комплексній площині і являє собою геометричне місце кінців векторів динамічної податливості при зміні ω від 0 до ∞. По речовинній осі для кожної частоти відкладений компонент податливості, що збігається по фазі з напрямком дії сили, а по уявній – компонента податливості, зсунута на по фазі щодо напрямку дії сили.

Довжина вектора, проведеного з початку координат у точку АФЧХ, дорівнює модулю динамічної податливості А(ω), а кут між цим вектором і напрямком дійсної осі – фазовий кут φ(ω).

При малому значенні відношення амплітуда змушених коливань лише небагато відрізняється від статичного переміщення . Якщо ж частота змушених коливань ω наближається до частоти власних коливань ω₀ системи, то при відсутності демпфірування амплітуда змушених коливань прагне до нескінченності. При резонансі (ω = ω₀₎ і наявності демпфірування А(ω) має кінцеве, збільшене значення. При ω > ω₀ амплітуда в₀ зменшується, при ω >> ω₀ стає дуже малою.

Рис. 3.3. Частотні характеристики одномасової системи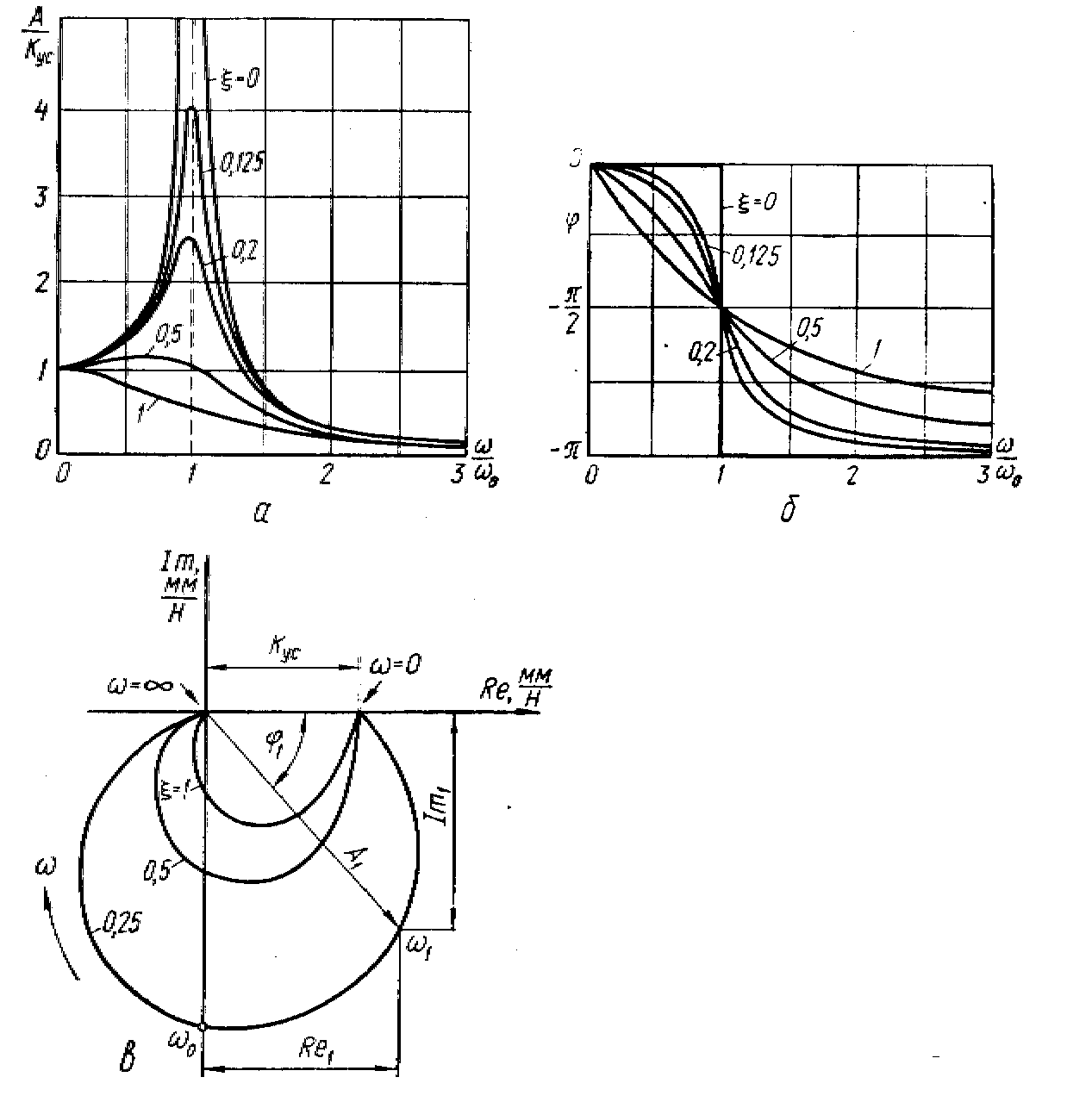

Вигляд АФЧХ визначається значенням відносного коефіцієнта демпфірування ξ. При малому демпфіруванні форма АФЧХ в основній своїй частині наближається до окружності, розташованої симетрично відносно уявної координати. Якщо демпфірування визначається внутрішнім тертям (гістерезисне демпфірування) і воно збігається по фазі зі швидкістю, але не пропорційно її значенню, а пропорційно переміщенню, то основна частина АФЧХ являє собою окружність. Діаметр, розташований на мнимій осі, що відповідає резонансу, є мірою демпфірування системи.

Відношення є коефіцієнтом динамічності системи.

Метод механічних ланцюгів

Рішення задач динаміки складних лінійних механічних систем з багатьма ступенями свободи в багатьох випадках можна спростити, застосувавши метод механічних ланцюгів. Розрахункова схема механічного ланцюга, що відповідає розглянутій механічній системі, складається з активних елементів – джерел сили (моменту) або швидкості з заданим законом зміни у часі і пасивних елементів – мас (моментів інерції), опорів – демпферів і пружностей.

Кожен елемент механічного ланцюга розглядається як двополюсник. Позначення елементів на схемах показані на рис. 3.4. Рух маси розглядається відносно нерухомої системи координат. Тому позначення маси (прямокутник) дається в сполученні із символом нерухомої системи координат (куточком). Полюс b елемента маси, зв'язаний з кутом, має швидкість, рівну нулю.

1 2 3 4 5

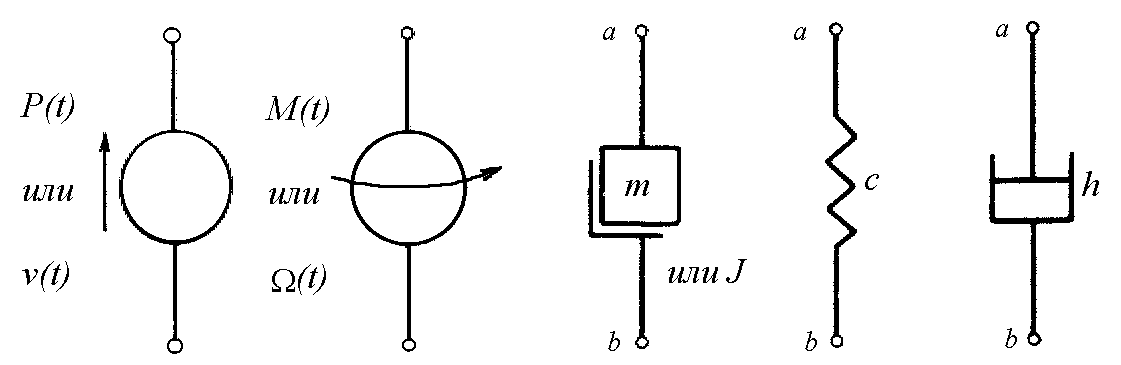
Рис. 3.4. Елементи механічних ланцюгів:

1 – джерело сили або швидкості при поступальному русі: 2 – джерело моменту чи кутової швидкості; 3 – маса або момент інерції; 4 – пружність; 5 – демпфер з в'язким опором

Прийнято переміщення s і швидкість v полюсів-кінців елементів позначати індексами, що відповідають позначенням цих полюсів.

Сила інерції маси m визначається рівнянням

(3.8)

де – оператор диференціювання.

Сила пружності

(3.9)

Сила демпфірування

(3.10)

При складанні розрахункових схем механічних ланцюгів кінці елементів, що рухаються спільно і мають однакові швидкості, з'єднують у спільні вузли. Один з кінців кожного елемента – маси, що має нульову швидкість, з'єднують з базою відліку – системою координат. Один з кінців джерела сили (моменту) чи швидкості також з'єднують з базою відліку. Розрахунок механічних ланцюгів ведуть відносно їхніх рівноважних станів. Тому сила ваги та інші постійні сили не враховуються. При розрахунку механізмів обертального руху в рівняння входять тільки перемінні швидкості, створювані перемінними складовими моментів, і аналіз механічних ланцюгів виробляється в рівномірно обертовій системі координат, щодо якої система замкнута.

При розрахунку механічних ланцюгів на основі принципу Даламбера і загального рівняння динаміки складається рівняння балансу сил (моментів) вузла чи швидкостей контуру:

для балансу сил (моментів) вузла алгебраїчна сума всіх сил (моментів), прикладених до кожного вузла з'єднання елементів механічного ланцюга, дорівнює нулю;

для балансу швидкостей контуру алгебраїчна сума усіх швидкостей елементів замкненого механічного ланцюга дорівнює нулю.

Ці рівняння аналогічні рівнянням законів Кірхгофа для електричних ланцюгів.

Якщо рух створюється джерелом сили (моменту), то складаються рівняння балансу сил (моментів) вузлів, а якщо джерелом швидкості – рівняння балансу швидкостей контурів.

При розрахунку механічних ланцюгів будемо позначати переміщення і швидкості вузлів буквами s і v з індексами відповідних вузлів.

Для механічної системи, що складається з маси т, пружин с₁ і с₂, демпфера h (рис. 3.5 а), розрахункова схема механічної системи дана на рис. 5 б.

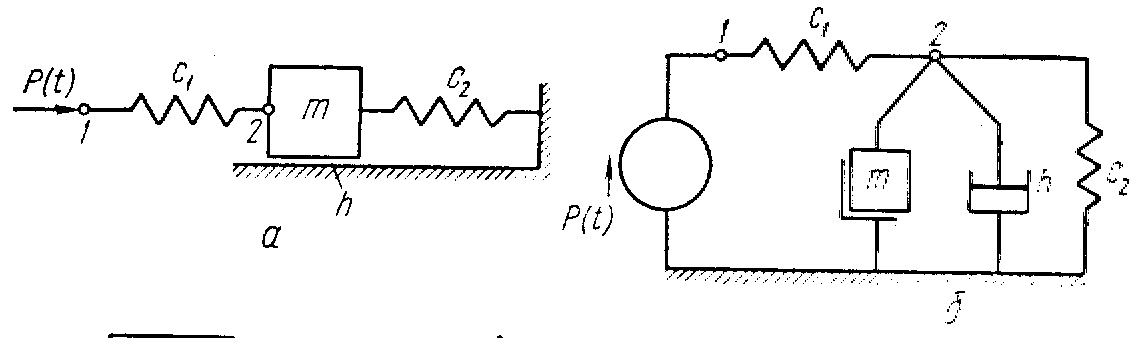
Рис. 3.5. Схеми механічних ланцюгів систем з поступальним рухом

Баланс сил у вузлі 1

(3.11)

Баланс сил у вузлі 2

(3.12)

З цих рівнянь можуть бути отримані різні передатні функції системи (у залежності від того, яка величина прийнята як вхід і яка – як вихід).

Визначимо динамічну податливість . З рівняння (3.12)

Після підстановки в рівняння значення s₂ і перетворень

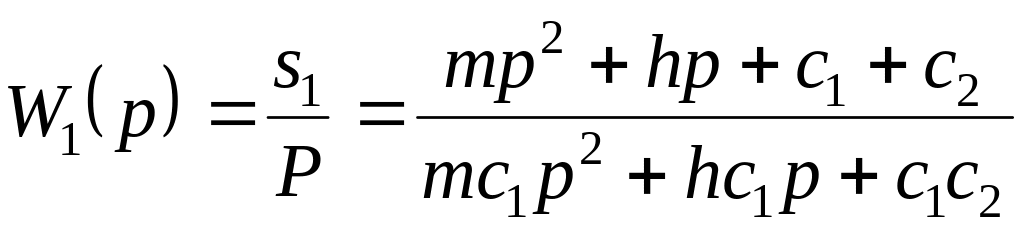
Розділимо чисельник і знаменник отриманого виразу передатної функції на с₁с₂, щоб останній член знаменника дорівнював одиниці, як це звичайно прийнято. Тоді

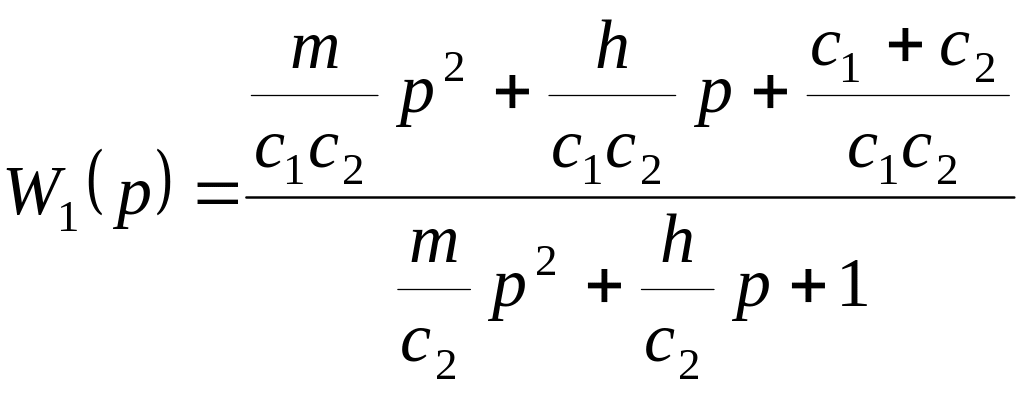
У статичному режимі, коли р = 0, податливість системи дорівнює

Аналогічно одержуємо передатну функцію