
- •Часть I Введение
- •I. Матрицы.
- •1. Основные понятия.
- •2. Действия над матрицами
- •2. Определители
- •1. Основные понятия
- •2. Свойства определителей (необходимы для вычисления определителей):
- •3. Невырожденные матрицы
- •2. Ранг матрицы
- •II. Система линейных уравнений.
- •1. Основные понятия
- •2. Решение системы линейных уравнений
- •3. Решение не вырожденных линейных систем.
- •4. Метод Гаусса
- •5. Система однородных линейных уравнений
- •6.Модель Леонтьева многоотраслевой экономики
- •III. Элементы векторной алгебры
- •1. Основные понятия
- •2. Операции над векторами
- •3. Векторное пространство и п – мерный вектор
- •3.1. Линейная зависимость векторов
- •Размерность и базис линейного пространства.
- •3.3. Разложение вектора в ортогональном базисе.
- •3.4.Переход к новому базису.
- •3.5. Линейные операторы.
- •3.6. Собственные векторы и собственные значения линейного оператора.
- •2. Симметричный оператор.
- •3. Ортогональность собственных векторов.
- •3.7.Квадратичные формы.
- •IV Аналитическая геометрия на плоскости.
- •1.Система координат. Основные понятия.
- •Линия на плоскости(основные понятия)
- •2. Уравнение прямой на плоскости
- •1) Уравнение прямой с угловым коэффициентом
- •2) Общее уравнение прямой X
- •7) Нормальное уравнение прямой
- •8) Угол между двумя прямыми
- •9) Точка пересечения прямых
- •10) Расстояние от точки до прямой
- •3.Линии второго порядка на плоскости.
- •1) Окружность
- •2) Эллипс
- •3) Гипербола.
- •Исследование формы гиперболы по ее уравнению
- •Асимптоты гиперболы
- •4) Парабола
- •Исследование формы параболы по ее уравнению
- •5) Общее уравнение линий второго порядка
- •V Аналитическая геометрия в пространстве
- •1. Уравнение поверхности и линии в пространстве
- •2.Поверхности второго порядка
- •VI. Основы математического анализа
- •1. Множества. Действительные числа
- •6. Предел функции
- •1) Предел функции в точке
- •2) Предел функции при X→∞.
- •3) Бесконечно большая функция (б.Б.Ф.).
- •4) Бесконечно малые функции.
- •6) Признаки существования пределов.
- •7) Первый замечательный предел.
- •8. Комплексные числа
4. Метод Гаусса
(решение систем линейных уравнений)
Одним из наиболее универсальных и эффективных методов решения систем линейных уравнений является метод Гаусса, заключающийся в последовательном исключении неизвестных.
Пусть дана система уравнений:
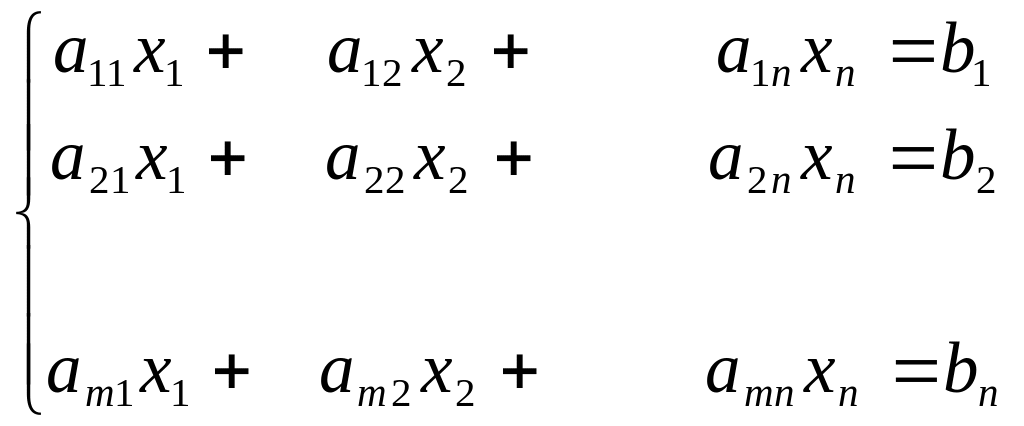
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Опишем все это поподробнее:
Прямой ход. Будем считать, что
а11 ≠ 0 (если а11
= 0, то переставим строки так, чтобы
первый элемент
![]() не был равен 0), после этого
преобразуем систему исключив неизвестное
х1 во всех уравнениях,
кроме первого. (для чего умножим обе
части первого уравнения на (
не был равен 0), после этого
преобразуем систему исключив неизвестное
х1 во всех уравнениях,
кроме первого. (для чего умножим обе
части первого уравнения на (![]() )
и сложим полученное со вторым уравнением
системы). Затем умножим обе части первого
уравнения на (
)
и сложим полученное со вторым уравнением
системы). Затем умножим обе части первого
уравнения на (![]() ) и сложим с третьим уравнением системы.
Продолжая этот процесс получим
окончательно:
) и сложим с третьим уравнением системы.
Продолжая этот процесс получим
окончательно:
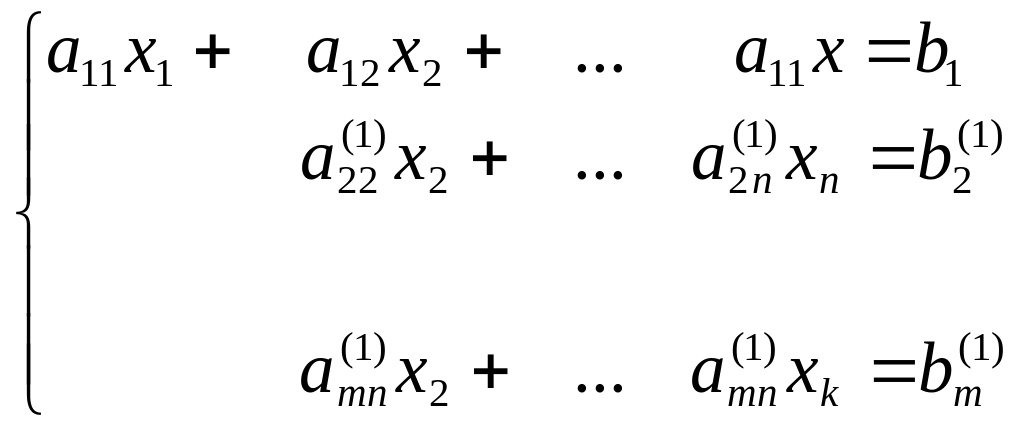
Здесь
![]() – новые значения коэффициентов и правых
частей, которые получаются после первого
шага.
– новые значения коэффициентов и правых
частей, которые получаются после первого
шага.
Аналогичным образом, считая главным
элементом
![]() исключим х2 из всех
уравнений системы кроме первого и
второго и так далее. Продолжаем этот
процесс пока возможно. Если в процессе
приведения системы к ступенчатому виду
появится нулевое уравнение т.е. равенство
вида 0 = 0, их отбрасывают. Если же появится
уравнение вида 0 = bi
, а bi
≠ 0, то это говорит о несовместимости
системы.
исключим х2 из всех
уравнений системы кроме первого и
второго и так далее. Продолжаем этот
процесс пока возможно. Если в процессе
приведения системы к ступенчатому виду
появится нулевое уравнение т.е. равенство
вида 0 = 0, их отбрасывают. Если же появится
уравнение вида 0 = bi
, а bi
≠ 0, то это говорит о несовместимости
системы.
Проведя все эти операции до конца, получим следующую систему уравнений:
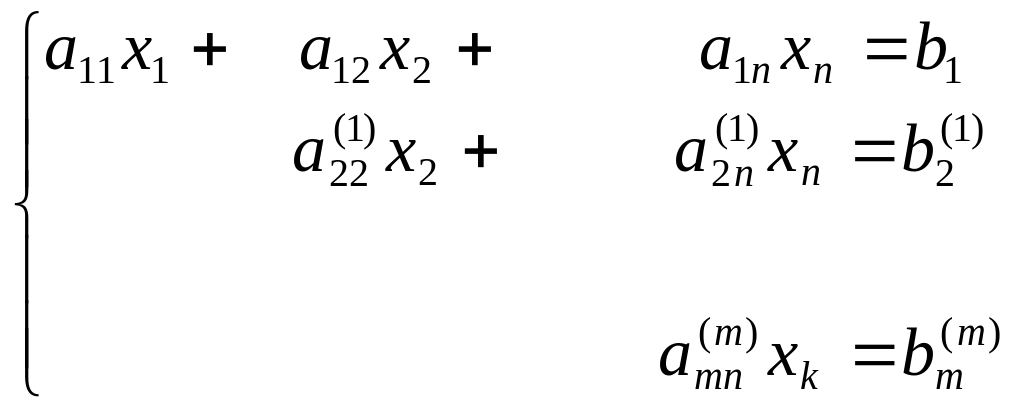

где k < n, aii ≠ 0, i = 1к. Коэффициенты aii называются главными элементами системы.
Второй этап заключается в решении ступенчатой системы уравнений. Она, вообще говоря, имеет бесчисленное множество решений.
В последнем уравнении этой системы
выражаем первое неизвестное
![]() через остальные неизвестные (хk+1
… xn).
Затем подставляем значение Хk
в предпоследнее уравнение системы
и выражаем xk-1
через (хk+1 …
xn),
затем находим xk-2
…х1. Придавая свободным неизвестным
(хk+1 … xn)
произвольные значения получим бесчисленное
множество решений системы.
через остальные неизвестные (хk+1
… xn).
Затем подставляем значение Хk
в предпоследнее уравнение системы
и выражаем xk-1
через (хk+1 …
xn),
затем находим xk-2
…х1. Придавая свободным неизвестным
(хk+1 … xn)
произвольные значения получим бесчисленное
множество решений системы.
Пример:
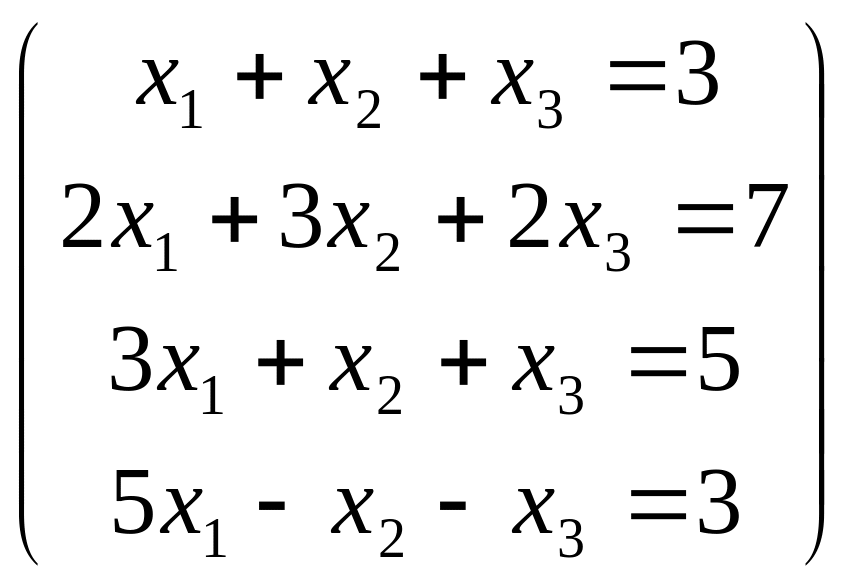
Решение: Произведем элементарные преобразования над строчками расширенной матрицы системы:
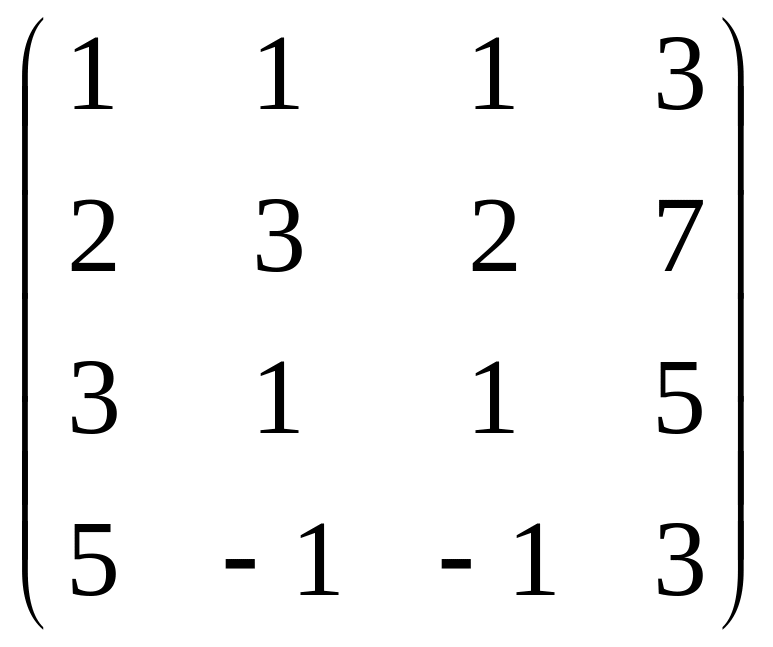 ~
~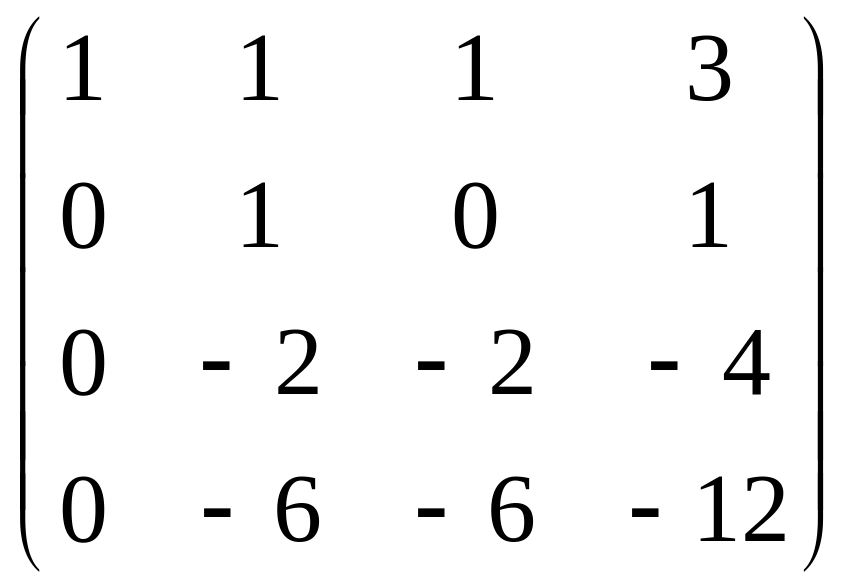 ~
~ ~
~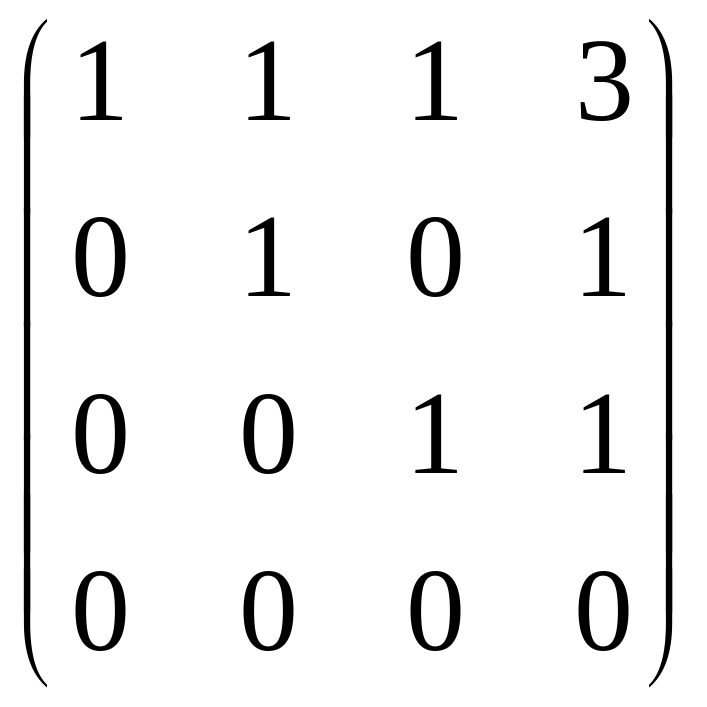
Полученная матрица соответствует системе:
 итого
итого
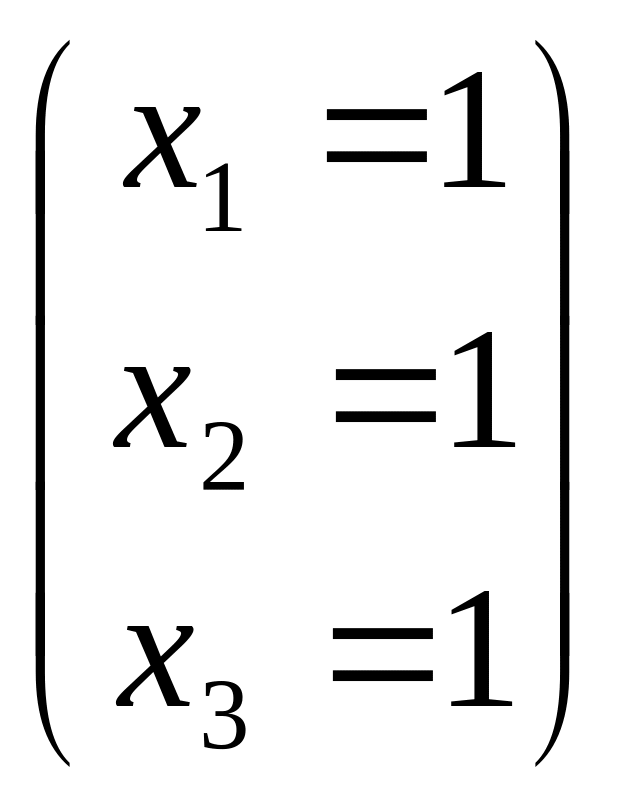
5. Система однородных линейных уравнений
Пусть дана система однородных линейных уравнений:

Очевидно, что однородная система всегда совместна (r(A) = r(Ā)), т.к. она имеет нулевое решение х1=х2=…хп=0
При каких условиях однородная система имеет и ненулевое решение?
Теорема Для того. Чтобы система однородных уравнений имела ненулевое решение необходимо и достаточно, чтобы ранг r её основной матрицы был меньше числа n неизвестных т.е. r<n.
Необходимость. Так как r не
может превосходить размера матрицы, то
очевидно r ≤ n.
Пусть r = n. Тогда
один из миноров размера п×п отличен
от нуля. Поэтому соответствующая система
линейных уравнений имеет единственное
решение
![]() , ∆i=0, ∆≠0. Значит,
других, кроме тривиальных решений нет.
Итак если есть нетривиальное решение,
то r<n.
, ∆i=0, ∆≠0. Значит,
других, кроме тривиальных решений нет.
Итак если есть нетривиальное решение,
то r<n.
Достаточность. Пусть r<n, но тогда, поскольку ранг системы меньше числа её неизвестных, эта система имеет бесконечно много решений, а значит и хотя бы одно нулевое решение, о чем говорилось выше (теорема 3) два следствия вытекают из этой теоремы.
Следствие 1 Если число уравнений однородной системы меньше числа её неизвестных, то система имеет нулевое решение.
Следствие 2 Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение, тогда и только тогда когда ∆=0.
