
- •Дискретная математика. Теория и практика
- •Оглавление
- •Глава 1. Множества 6
- •Глава 2. Комбинаторика 24
- •Глава 3. Отношения. Отображения 34
- •Глава 4. Алгебраические структуры 55
- •Предисловие
- •Введение
- •Глава 1. Множества
- •1.1. Множества и их элементы. Способы задания множеств
- •1.2. Подмножества
- •1.3. Операции над множествами
- •1.4. Диаграммы Эйлера – Венна
- •1.5. Прямое произведение множеств
- •1.6. Метод математической индукции
- •1.7. Соответствия
- •1.8. Задачи, связанные с определением мощности конечного множества
- •Задачи и упражнения к главе 1
- •Глава 2. Комбинаторика
- •2.1. Правила суммы и произведения
- •2.2. Размещения и сочетания
- •2.3. Примеры решения задач
- •2.4. Бином Ньютона
- •2.5. Свойства биномиальных коэффициентов. Треугольник Паскаля
- •Задачи и упражнения к главе 2
- •Глава 3. Отношения. Отображения
- •3.1. Понятие отношения
- •3.2. Способы задания бинарных отношений
- •Характеристическим свойством.
- •3.3. Операции над бинарными отношениями
- •3.4. Свойства матриц бинарных отношений
- •3.5. Свойства бинарных отношений
- •3.6. Определение свойств бинарного отношения по его матрице
- •3.7. Отношение эквивалентности
- •3.8. Счетные и несчетные множества
- •3.9. Отношение порядка. Диаграммы Хассе
- •3.10. Функции
- •Задачи и упражнения к главе 3
- •Глава 4. Алгебраические структуры
- •4.1. Алгебраические операции и их свойства
- •4.2. Понятие алгебраической структуры
- •4.3. Алгебры с одной бинарной алгебраической операцией
- •4.4. Алгебры с двумя бинарными алгебраическими операциями
- •4.5. Конечные поля
- •4.6. Булевы алгебры
- •4.7. Гомоморфизмы алгебр
- •4.8. Алгебраические системы. Решетки
- •Задачи к главе 4
- •Список литературы
4.4. Алгебры с двумя бинарными алгебраическими операциями
Среди алгебр с двумя бинарными алгебраическими операциями особо выделяются кольца и поля.
Определение 4.21. Алгебра А = < А, +, ∙ > называется ассоциативным кольцом с единицей, если выполняются следующие условия (аксиомы):
алгебра < A, + > есть коммутативная аддитивная группа;
алгебра < A, ∙ > есть мультипликативный моноид;
умножение дистрибутивно относительно сложения, то есть
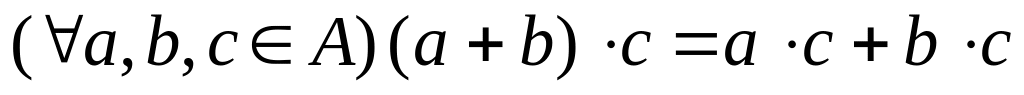 и
и
 .
.
Замечание 4.5. В дальнейшем под словом «кольцо» будем подразумевать ассоциативное кольцо с единицей.
Элементы множества А называются элементами кольца А = < А, +, ∙ >.
Определение 4.22. Группа < A, + > называется аддитивной группой кольца А = < А, +, ∙ >. Нейтральный элемент относительно сложения называется нулем кольца и обозначается через 0 или 0А.
Определение 4.23. Моноид < A, ∙ > называется мультипликативным моноидом кольца А = < А, +, ∙ >. Нейтральный элемент относительно умножения называется единицей кольца А и обозначается через 1 или 1А.
Определение
4.24. Кольцо
называется коммутативным,
если операция умножения коммутативна,
т.е.
![]() .
.
Пример 4.14. Алгебра < Z, +, ∙ > образует коммутативное кольцо целых чисел.
Определение 4.25. Полем называется коммутативное кольцо, в котором нуль кольца отличен от единицы кольца и для каждого ненулевого элемента существует обратный к нему относительно операции умножения.
Пример 4.15. Кольцо целых чисел < Z, +, ∙ > полем не является, так как ни один ненулевой элемент, кроме 1, не обладает обратным к нему.
Пример 4.16. Множества Q, R и С образуют бесконечные поля относительно обычных операций сложения и умножения, которые соответственно называются полем рациональных чисел, полем действительных чисел и полем комплексных чисел.
Пример
4.17. Выяснить,
образует ли алгебра <![]() >
>
кольцо, поле?
Решение. Докажем сначала, что операции сложения и умножения матриц являются бинарными алгебраическими операциями на множестве
М
=
![]() .
Для
этого
достаточно показать замкнутость
множества М
относительно этих операций.
.
Для
этого
достаточно показать замкнутость
множества М
относительно этих операций.
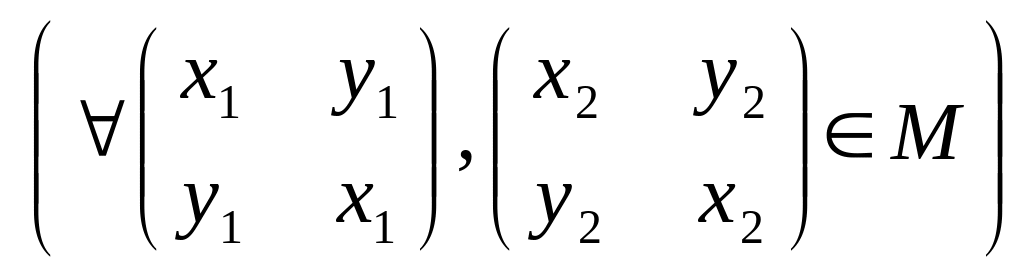
![]()
![]() =
=
![]()
M.
M.
Следовательно, операции «+» и «» – бинарные алгебраические операции на М.
Сложение
произвольных матриц (если оно определено)
коммутативно и ассоциативно. Значит,
«+» коммутативно и ассоциативно на М.
Очевидно, что матрица
![]()
М
есть нейтральный элемент относительно
«+», а
М
есть нейтральный элемент относительно
«+», а
![]() М
– противоположный элемент для произвольной
матрицы
М
– противоположный элемент для произвольной
матрицы
![]() из множества М.
Следовательно, < М,
+ > – коммутативная группа.
из множества М.
Следовательно, < М,
+ > – коммутативная группа.
Умножение произвольных матриц (если оно определено), а значит и матриц из множества М, является ассоциативной операцией. Пусть – произвольная матрица из множества М.
![]() =
=
![]() =
=
![]()
b
=
![]() при x
0. Отсюда xa
+
при x
0. Отсюда xa
+
![]() = x.
Выполним преобразования:
= x.
Выполним преобразования:
x2a
+ y2
– y2a
= x2
y2
(1
–
a)
= x2
(1
–
a)
1
–
a
= 0
a
= 1
b
=
![]() =
0.
=
0.
Если
x
=
0, то
![]() .
Так как y
– произвольное действительное число,
то и в этом случае получаем, что a
= 1 и b
= 0. Получили, что
.
Так как y
– произвольное действительное число,
то и в этом случае получаем, что a
= 1 и b
= 0. Получили, что
![]() М
– нейтральный элемент относительно
«».
Следовательно,
М
– нейтральный элемент относительно
«».
Следовательно,
< М, > – моноид.
Известно, что умножение дистрибутивно относительно сложения для произвольных матриц (если операции имеют смысл), в частности, и для матриц из множества М.
Таким образом, алгебра < М, +, > – кольцо.
![]() =
=![]() =
=
=
=![]() .
.
Получили, что «» – коммутативно. Следовательно, кольцо коммутативно. Нуль кольца отличен от единицы кольца: ≠ . Выясним, для каждого ли ненулевого элемента из множества М существует обратный к нему. Легко видеть, что роль обратного элемента к матрице из М играет обратная к ней матрица.
![]()
![]()
![]() ≠
0
x2
–
y2
≠
0
x2
y2
x
±
y.
≠
0
x2
–
y2
≠
0
x2
y2
x
±
y.
Значит,
множество М
содержит ненулевые матрицы, например
матрицу
![]() ,
для которых не существуют обратные к
ним.
,
для которых не существуют обратные к
ним.
Итак, алгебра < М, +, > образует коммутативное кольцо, но не является полем.
