
- •Задачи а
- •6. Найти общее решение дифференциального уравнения .
- •16. Является ли функция решением уравнения ?
- •10.2. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
- •5. Решить задачу Коши: .
- •10.3. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •Задачи а
- •5. Решить задачу Коши:
- •18. Решить задачу Коши: .
- •10.4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами со специальной правой частью
- •2. Решить задачу Коши .
- •14. Решить задачу Коши .
- •19. Решить задачу Коши .
- •10.5. Численные методы решения дифференциальных уравнений: метод Эйлера, метод Рунге – Кутты
- •Задания для выполнения лабораторной работы
- •Решение типовых задач
- •Контрольные задания по теме «Дифференциальные уравнения»
- •4. Найти общее решение дифференциального уравнения .
- •6. Найти общее решение дифференциального уравнения
- •12. Найти общее решение дифференциального уравнения .
5. Решить задачу Коши: .
Домашнее задание
Решить дифференциальные уравнения:
6.
![]() .
7.
.
7.
 .
.
Решить задачу Коши:
8.
 .
9.
.
9.
![]() .
.
Дополнительные задачи
Решить дифференциальные уравнения:
10.
![]() .
11.
.
11.
![]() . 12.
. 12.
![]() .
.
Решение типовых задач
Пример
1.
Решить уравнение
![]() .
.
Это линейное дифференциальное уравнение.
Полагаем
![]() ,
тогда
,
тогда
![]() и уравнение принимает вид
и уравнение принимает вид
![]() или
или
![]() .
(10.2)
.
(10.2)
Функцию
![]() найдем из условия, чтобы обращался в
нуль коэффициент при
найдем из условия, чтобы обращался в
нуль коэффициент при
![]() в
уравнении (10.2):
в
уравнении (10.2):
![]() .
.
Это уравнение с разделяющимися переменными. Тогда
![]() ,
,
откуда находим любое отличное от нуля решение:
![]() .
.
Подставляя найденную функцию в (10.2), получим:
![]() ,
,
![]() ,
,
Откуда
![]() .
Следовательно, общее решение данного
дифференциального уравнения:
.
Следовательно, общее решение данного
дифференциального уравнения:
![]() .
.
Ответы
2.
 3.
3.
 4.
4. ![]() .
5.
.
5. ![]() .
6.
.
6. ![]() .
7.
.
7. ![]() .
8.
.
8.  .
9.
.
9.  .
10.
.
10. ![]() .
11.
.
11. ![]() .
12.
.
12. ![]() .
.
10.3. Дифференциальные уравнения второго порядка, допускающие понижение порядка
Основные понятия: дифференциальное уравнение второго порядка, решение, общее решение, общий интеграл, задача Коши, частное решение, теорема существования и единственности решения задачи Коши; уравнения, допускающие понижения порядка [1, стр. 431-435].
Дифференциальное уравнение второго
порядка относительно искомой функции
![]() в общем случае записывается в виде
в общем случае записывается в виде
![]()
или, если это возможно, в виде, разрешенном
относительно второй производной
![]() .
.
I. Простейшее уравнение
2-го порядка:![]() .
.
Решение этого уравнения получается путем двукратного интегрирования.
II. Уравнения, не содержащие
явно неизвестной функции
![]() это уравнения вида
это уравнения вида
![]() .
.
Порядок уравнения понижают, полагая
![]() ,
тогда
,
тогда
![]() .
.
III. Уравнения, не содержащие
явно независимой переменной имеют вид:
![]() Порядок уравнения понижают, полагая
Порядок уравнения понижают, полагая
![]() ,
тогда
,
тогда
 .
.
Задачи а
1. Проверить,
является ли функция
![]() решением дифференциального
уравнения
решением дифференциального
уравнения
![]() .
.
2.
Показать, что уравнение
![]() имеет интегральные кривые
имеет интегральные кривые
![]() и
и
![]() ,
пересекающиеся в точке
,
пересекающиеся в точке
![]() Противоречит ли это
теореме существования и единственности
решения задачи Коши?
Противоречит ли это
теореме существования и единственности
решения задачи Коши?
3. Используя методы понижения порядка, свести к уравнениям первого порядка следующие дифференциальные уравнения:
а)
![]() ;
б)
;
б)
![]() ; в)
; в)
 ;
;
г)
![]() ;
д)
;
д)![]() ; е)
; е)
![]() .
.
4. Найти
общее решение уравнения
![]() .
.
Задачи Б
5. Решить задачу Коши:
Решить уравнения:
6.
![]() .
7.
.
7.
![]() .
.
Решить задачу Коши:
8.
![]() 9.
9.
![]()
Домашнее задание
Решить уравнения:
10.
![]() .
11.
.
11.
 .
.
Решить задачу Коши:
12.
![]() .
13.
.
13.
![]() .
.
Дополнительные задачи
Решить уравнения:
14.
![]() .
15.
.
15.
![]() .
.
16.
![]() . 17.
. 17.
![]() .
.
18. Решить задачу Коши: .
Решение типовых задач
Пример 1. Найти общее решение уравнения
 .
.
Последовательно интегрируя два раза данное уравнение, получим
 ,
,
![]() ,
,
![]() .
.
Пример 2. Найти частное решение
уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Полагаем , тогда и уравнение принимает вид
![]() или
или
 Это линейное уравнение
относительно функции
Это линейное уравнение
относительно функции
![]() Найдем решение этого уравнения методом
Бернулли. Полагаем
Найдем решение этого уравнения методом
Бернулли. Полагаем
![]() Имеем:
Имеем:
![]() или
или
 .
Подберем функцию
.
Подберем функцию
![]() так, чтобы
так, чтобы
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
Получаем
.
Получаем
![]() ,
,
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() .
Из условия
.
Из условия
![]() получаем
получаем
![]()
![]()
![]() .
Имеем
.
Имеем
![]() или
или
![]() .
Интегрируя, получим
.
Интегрируя, получим
 .
Находим
.
Находим
![]() из
начальных условий:
из
начальных условий:
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
 искомое
частное решение.
искомое
частное решение.
Пример 3. Найти частное решение
уравнения
 ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Полагаем
,
тогда
![]() и уравнение принимает вид
и уравнение принимает вид
 .
.
Так как
![]() (иначе
(иначе
![]() ,
что противоречит начальному условию
,
что противоречит начальному условию
![]() ),
то
),
то
 Это уравнение с разделяющимися
переменными. Решая его, получим
Это уравнение с разделяющимися
переменными. Решая его, получим
![]() .
Из начальных условий
.
Из начальных условий
![]() получаем
получаем
![]() .
Откуда имеем
.
Откуда имеем
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() .
Разделяя переменные и интегрируя,
получим
.
Разделяя переменные и интегрируя,
получим
![]() .
Из условия
находим
.
Из условия
находим
![]() .
Таким образом,
.
Таким образом,
![]() искомое
частное решение данного уравнения.
искомое
частное решение данного уравнения.
Ответы
5.
![]() .
6.
.
6.  .
7.
.
7.
![]() .
8.
.
8. ![]() .
9.
.
9.
![]() .
10.
.
10. ![]() .
11.
.
11. 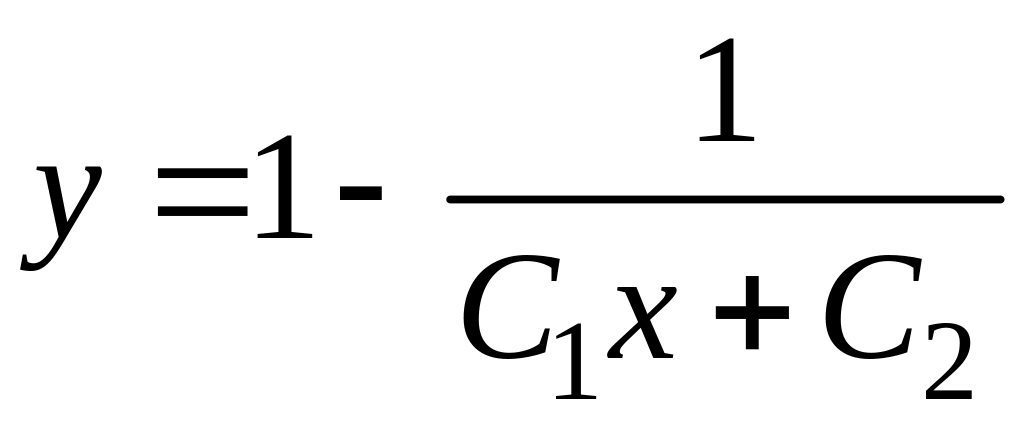 .
12.
.
12. ![]() .
13.
.
13.  .
14.
.
14. ![]() .
15.
.
15. ![]() .
16.
.
16. 
 .
17.
.
17. ![]() .
18.
.
18. ![]() .
.
