П.3 Свойства, связанные с отрезками интегрирования

Свойство 1 Если функция интегрируема на отрезке , то она интегрируема на любом отрезке .

Доказательство. Возьмем любое разбиение отрезка . Нужно доказать, что при .

Добавим к точки из так, чтобы .

Тогда , так как правая часть содержит все слагаемые левой части.

Устремим , тогда , но тогда , но тогда и . Значит, интегрируема на отрезке ■

Свойство 2 Если функция интегрируема на отрезке и , то

.

Доказательство. Существование интегралов следует из свойства 1. Равенство следует из того, что , где и – интегральные суммы на отрезках и , причем является точкой разбиения отрезка .

Если , то пределы интегральных сумм , , существуют и выполняется равенство, приведенное в формулировке теоремы ■

Верно и обратное утверждение: если интегрируема на отрезках и , то она интегрируема и на отрезке , и выполняется равенство из свойства 2.

Положим по определению , .

Свойство 3 Пусть функция интегрируема на отрезке . Тогда выполняется равенство:

.

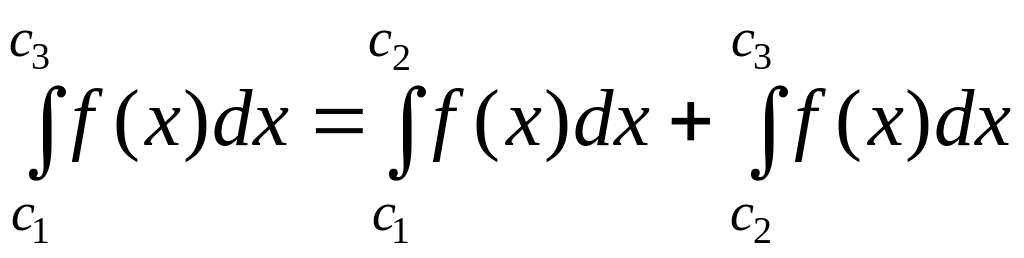Доказательство. Если , то равенство следует из свойства 2. Если , то так как 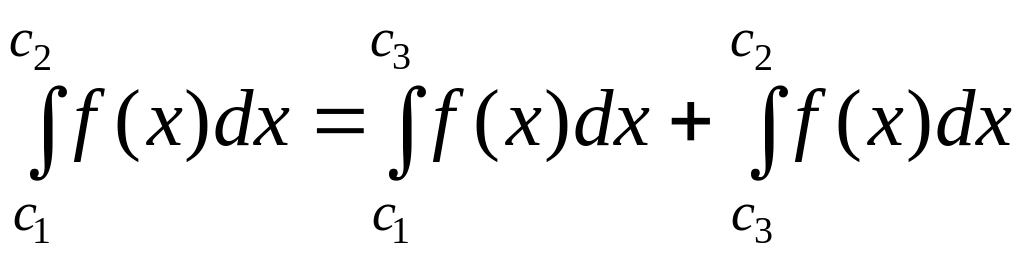, то отсюда ■

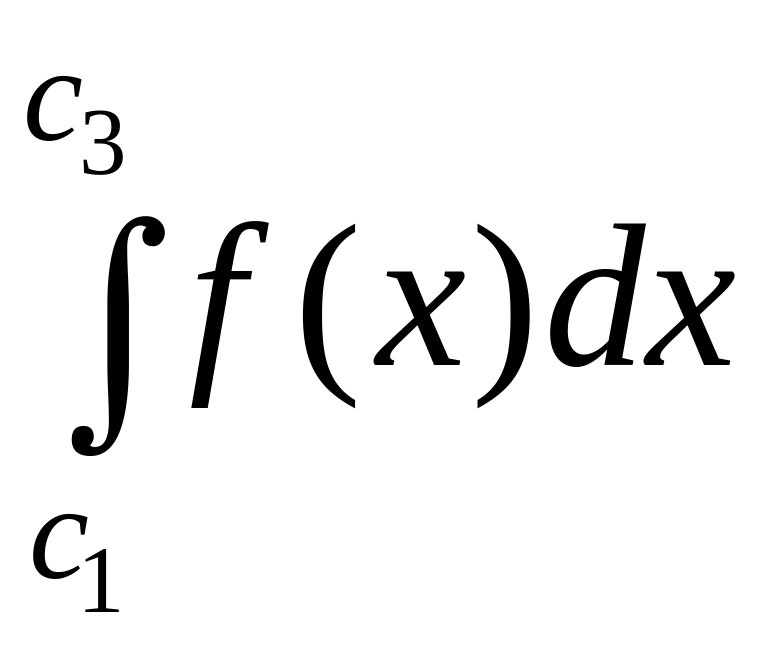
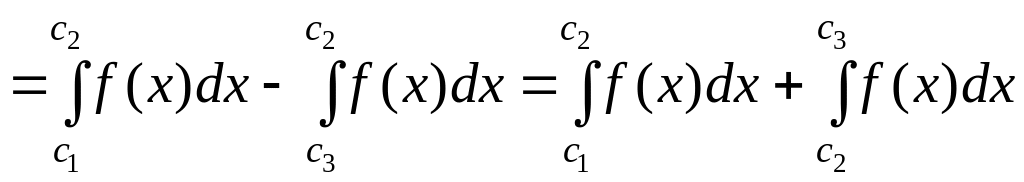П.4 Оценки интегралов

Теорема Если функция и интегрируема на отрезке , то .

Доказательство следует из того, что при условиях теоремы любая интегральная сумма ■

Следствие 1 (о монотонности интеграла) Если функции и интегрируемы на отрезке и если , то

.

Доказательство следует из того, что при условиях теоремы при любом разбиении ■

Следствие 2 Пусть функция интегрируема на отрезке и . Тогда выполняется неравенство:

.

Доказательство. . Левая часть неравенства доказывается аналогично ■

Теорема Если функция интегрируема на отрезке , то функция тоже интегрируема на и верна оценка:

.

Доказательство. Воспользуемся неравенством:

.

Тогда при любом разбиении .

Если при , то и . Значит, интегрируема на .

Рассмотрим неравенство .

Перейдем в нем к пределу при . Так как левая часть неравенства стремится к , а правая – к , то получим то, что и требовалось доказать ■

П.5 Интегральная теорема о среднем

Теорема Если функции и интегрируемы на отрезке , R : , функция не меняет своего знака на отрезке , тогда .

Если, кроме того, непрерывна на , то

.

Доказательство. Будем считать, что . Согласно свойству монотонности интеграла, .

Разделим все части последнего неравенства на . Получим

.

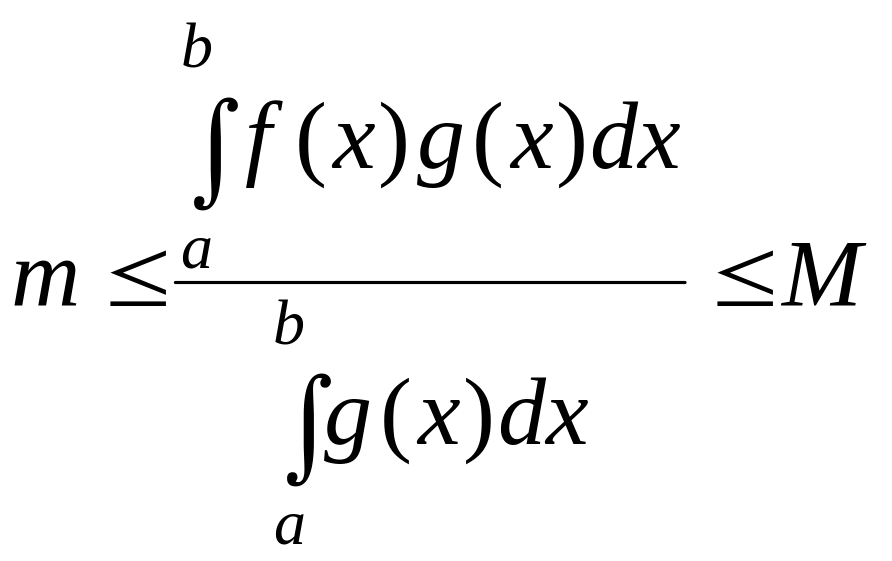Обозначив 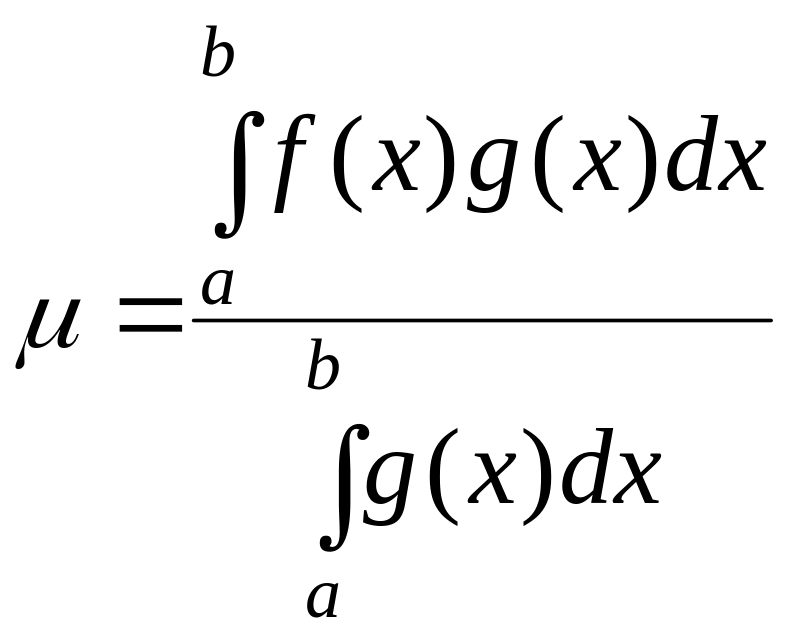, получим, что и требовалось доказать ■

Следствие Если функция интегрируема на отрезке и выполняется неравенство , то . Если, кроме того, непрерывна на , то

.

§ 5 Интеграл с переменным верхним пределом

Формула Ньютона-Лейбница

П.1 Определение и свойства интеграла с переменным верхним пределом

Если функция интегрируема на отрезке , то существует интеграл .

О. Функция называется интегралом с переменным верхним пределом.

Теорема 1 Если функция интегрируема на отрезке , то интеграл с переменным верхним пределом есть функция, непрерывная на этом отрезке.

Доказательство. Пусть и . Функция непрерывна в точке х, если при .

.

Так как интегрируема на , то она ограничена на , т.е.

.

Тогда .

Отсюда следует, что при , т.е. непрерывна в точке х. Т.к. х – произвольная точка из , то непрерывна на ■

Теорема 2 Если функция интегрируема на отрезке и непре-рывна в точке , то функция дифференцируема в точке , причем .

Доказательство. Пусть и . Докажем, что при . Воспользуемся тем, что

, .

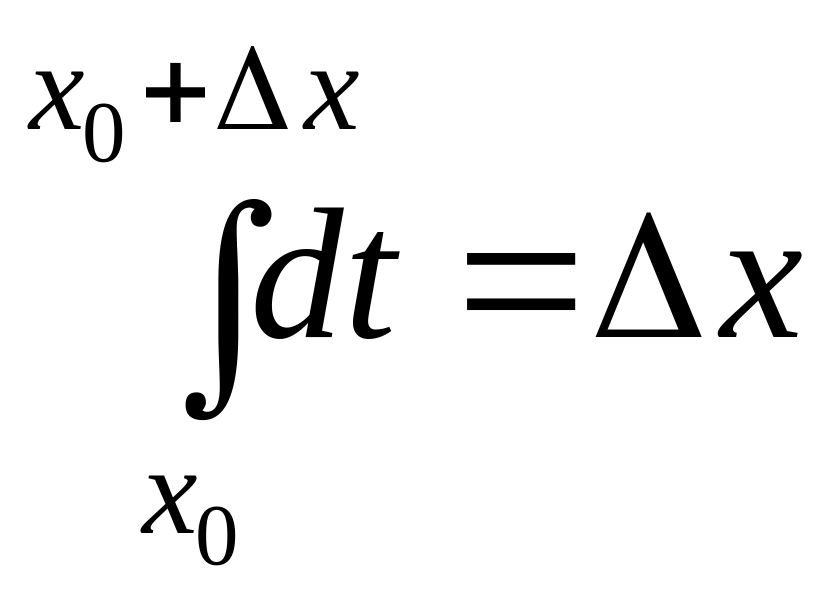В силу свойств интеграла,

.

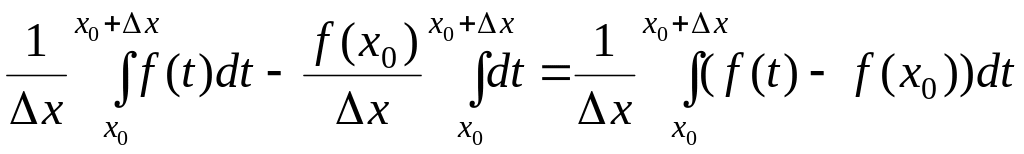Отсюда .

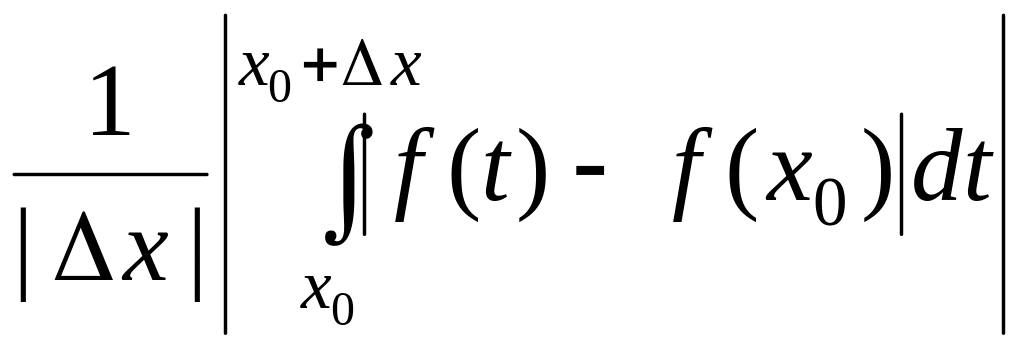Так как непрерывна в точке , то

.

Возьмем , тогда .

Таким образом, .

Значит, при . А это означает, что ■

Теорема 3 (о существовании первообразной у непрерывной функции) Если функция непрерывна на отрезке , то она имеет первообразную на этом отрезке, причем первообразной для функции является интеграл с переменным верхним пределом, т.е.

.

Доказательство. Действительно, по теореме 2, . По определению первообразной, является первообразной для ■

Следствие Всякая первообразная для функции , непрерывной на отрезке , имеет вид: , .

п.2 Формула Ньютона-Лейбница

Теорема Если функция непрерывна на отрезке и если – какая-нибудь первообразная для функции на этом отрезке, то справедлива формула Ньютона-Лейбница:

.

Доказательство. Если – некоторая первообразная для функции , то R : , .

Подставим в это равенство . Получим . Значит, .

Подставим в последнее равенство , получим . Отсюда ■

Пример .