П.3 Вычисление объемов тел

а) Объем тела вращения.

Утверждение Пусть криволинейная трапеция вращается вокруг оси . Объем полученного тела вращения вычисляется по формуле:

.

Доказательство. Пусть такие же, что в пункте 1. при вращении вокруг оси фигур и получаются цилиндры радиусов , и высоты . Получим

.

Величины в правой и левой частях неравенства являются соответственно с нижней и верхней суммами Дарбу функции при разбиении Т. Поэтому при они стремятся к ■

б) Объем тела с заданными площадями поперечных сечений.

Пусть тело заключено между плоскостями, перпендикулярными оси и пересекающими эту ось в точках и . Обозначим через фигуру, получаемую в сечении тела плоскостью, перпендикулярной оси и проходящей через точку . Пусть при известна площадь фигуры , причем функция непрерывна на .

Утверждение При указанных выше условиях объем тела вычисляется по формуле:

.

Пример Вычислить объем эллипсоида .

Решение. Проведем плоскость, перпендикулярную оси , через точку .

В сечении получим эллипс . Запишем его уравнение в стандартном виде: .

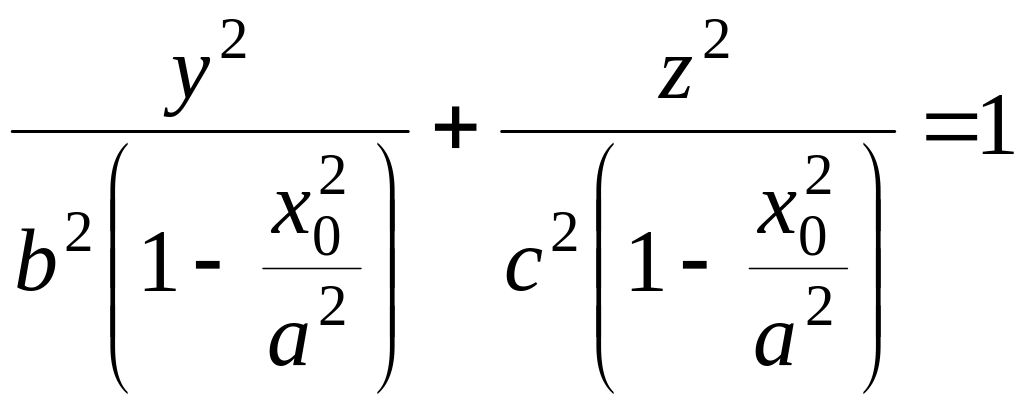Площадь эллипса, получаемого в сечении 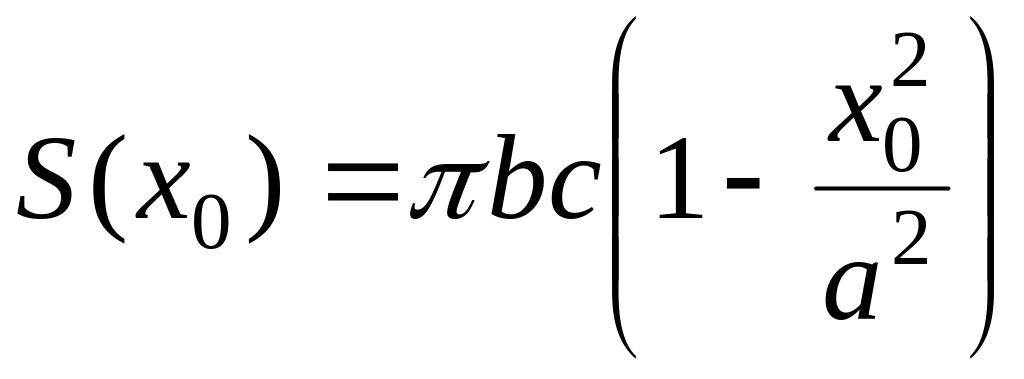. Тогда искомый объем

Аналогично рассуждая при получим объем шара .

П.4 Вычисление длины дуги кривой

Утверждение Если кривая Г задана уравнением

,

где непрерывно-дифференцируемые функции на , то длина кривой Г вычисляется по формуле:

.

Если кривая Г задана уравнением , то ее длина вычисляется по формуле:

.

Если кривая Г задана в полярных координатах , то длина кривой вычисляется по формуле:

.

П.5 Вычисление площади поверхности вращения

Утверждение Если функция имеет непрерывную производную на , то площадь поверхности вращения, образованной вращением графика функции вокруг оси , вычисляется по формуле:

.

Если поверхность получена вращением вокруг оси кривой, заданной параметрически: , то

.

Если вокруг оси вращается кривая, заданная в полярных координатах уравнением , то

.

§ 7 Несобственные интегралы п.1 Определения несобственных интегралов

Интеграл Римана мы определили на отрезке и для ограниченных функций. Распространим понятие интеграла на случай бесконечного промежутка интегрирования и на случай, когда подынтегральная функция не ограничена.

А) Интеграл на бесконечном промежутке.

Рассмотрим функцию . Она непрерывна на отрезке , значит, существует интеграл . Кроме того, существует . Этот предел называют несобственным интегралом от функции на промежутке и пишут .

. Пусть функция интегрируема на отрезке . Несобственным интегралом от функции на промежутке называется величина

.

Если последний предел существует и конечен, то несобственный интеграл называется сходящимся. В противном случае интеграл называется расходящимся.

. Интеграл определяется следующим образом:

,

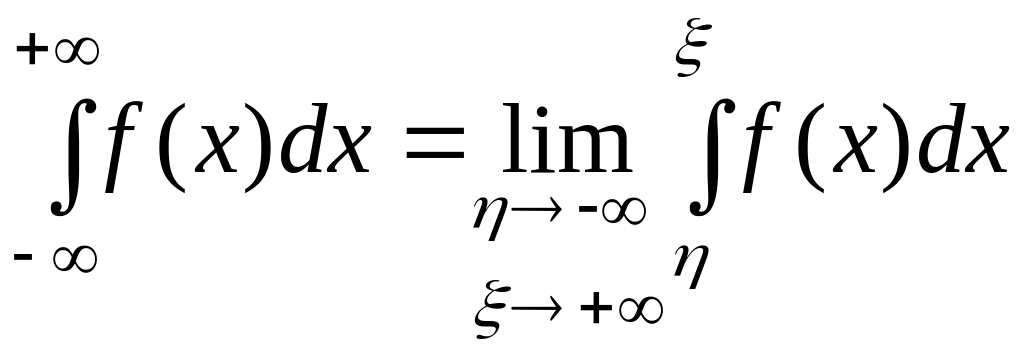причем предел не должен зависеть от того, каким образом и стремятся к и соответственно.

Пример Исследовать на сходимость интеграл .

Решение. Если , то .

Если , то

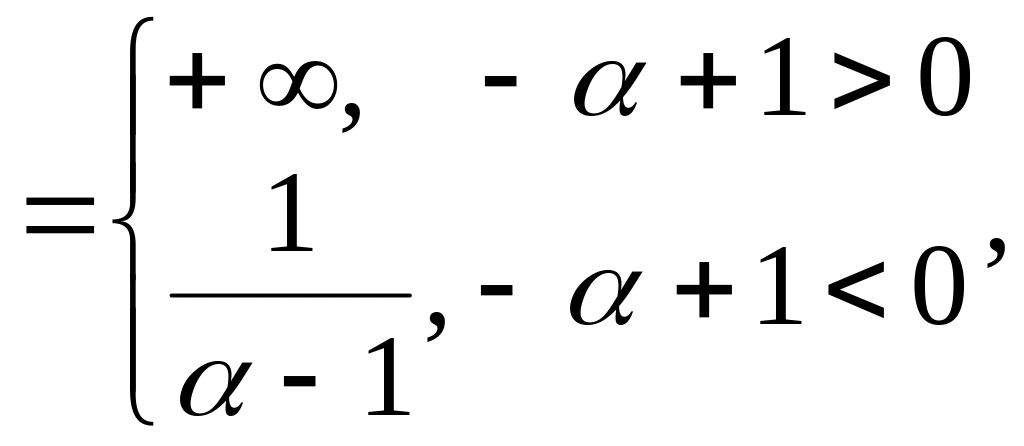т.е. .

Б) Интеграл на конечном промежутке от неограниченной функции.

Рассмотрим функцию . Она не ограничена на отрезке . Но при эта функция интегрируема на , причем

.

Рассмотрим . Этот предел называется несобственным интегралом от функции по отрезку .

. Пусть функция определена на конечном промежутке и интегрируема на отрезке . Несобственным интегралом от функции на промежутке называется величина

.

Если последний предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Пример Исследовать на сходимость интеграл .

Решение. Если , то

.

Если , то

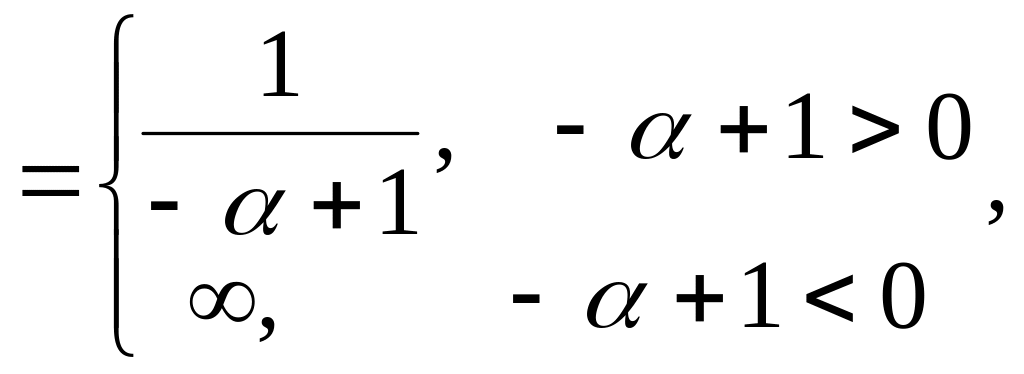т.е. .