
- •§ 3 Определенный интеграл п.1 Задачи, приводящие к понятию определенного интеграла
- •П.2 Определение интеграла Римана
- •П.3 Необходимое условие интегрируемости функции
- •П.4 Достаточное условие интегрируемости функции
- •П.5 Классы интегрируемых функций
- •§ 4 Свойства определенного интеграла п.1 Другая формулировка критерия интегрируемости
- •П.2 Свойства, связанные с операциями над функциями
- •П.3 Свойства, связанные с отрезками интегрирования
- •П.4 Оценки интегралов
- •П.5 Интегральная теорема о среднем
- •§ 5 Интеграл с переменным верхним пределом
- •П.1 Определение и свойства интеграла с переменным верхним пределом
- •П.3 Замена переменной в определенном интеграле
- •П.4 Интегрирование по частям в определенном интеграле
- •§ 6 Приложения определенного интеграла п.1 Вычисление площади плоской фигуры
- •П.2 Площадь криволинейного сектора
- •П.3 Вычисление объемов тел
- •П.4 Вычисление длины дуги кривой
- •П.5 Вычисление площади поверхности вращения
- •§ 7 Несобственные интегралы п.1 Определения несобственных интегралов
- •П.2 Свойства несобственных интегралов
- •П.3 Признаки сходимости несобственных интегралов
- •П.4 Абсолютно и условно сходящиеся интегралы
- •П.5 Признаки Дирихле и Абеля сходимости интегралов
П.2 Свойства несобственных интегралов
Будем рассматривать
несобственные интегралы вида
![]() ,
где
,
где
![]() особая точка интеграла (т. е.
особая точка интеграла (т. е.
![]() или
не ограничена в окрестности
или
не ограничена в окрестности
![]() ).
Будем предполагать, что
определена на
).
Будем предполагать, что
определена на
![]() и интегрируема на отрезке
.
и интегрируема на отрезке
.
1) Линейность.
Утверждение
Если сходятся несобственные интегралы
от функций
и
по
,
то при
![]() R
сходится
интеграл от функции
R
сходится
интеграл от функции
![]() на
и выполняется равенство:
на
и выполняется равенство:
![]()
![]() .
.
Доказательство.
Для
![]() ,
в силу свойств интеграла Римана,
выполняется равенство:
,
в силу свойств интеграла Римана,
выполняется равенство:
![]()
![]() .
.
Перейдем к пределу
в обеих частях последнего равенства
при
![]() .
Так как предел правой части существует
по условию теоремы, то существует предел
и левой части ■
.
Так как предел правой части существует
по условию теоремы, то существует предел
и левой части ■
2) Формула Ньютона-Лейбница.
Утверждение
Если функция
непрерывна на
и если
– первообразная для
,
то несобственный интеграл
сходится тогда, и только тогда, когда
существует и конечен
![]() ,
причем
,
причем
![]() .
.
Доказательство.
Так как
непрерывна на любом отрезке
![]() ,
где
,
где
![]() ,
то на
,
то на
![]() справедлива
формула
Ньютона-Лейбница:
справедлива
формула
Ньютона-Лейбница:
![]() .
.
Переходя в обеих частях последнего равенства к пределу при , получим, что и требовалось доказать ■
3) Интегрирование по частям.
Утверждение
Пусть функции
и
определены на
,
имеют непрерывные производные на
![]() .
Если существует и конечен
.
Если существует и конечен
![]() ,
а интеграл
,
а интеграл
![]() сходится, то интеграл
сходится, то интеграл
![]() тоже сходится и справедлива формула
интегрирования по частям:
тоже сходится и справедлива формула
интегрирования по частям:
![]() .
.
Доказательство аналогично доказательству предыдущего утверждения.
4) Формула замены переменной.
Утверждение
Если функция
непрерывна на
,
а функция
![]() непрерывно-дифференцируема на
непрерывно-дифференцируема на
![]() ,
строго возрастает и
,
,
строго возрастает и
,
![]() ,
то справедлива формула замены переменной:
,
то справедлива формула замены переменной:
![]() ,
,
при условии, что хотя бы один из интегралов сходится.
П.3 Признаки сходимости несобственных интегралов
Теорема 1
(критерий сходимости несобственного
интеграла от неотрицательной функции)
Если
![]()
![]() ,
то для сходимости несобственного
интеграла
,
то для сходимости несобственного
интеграла
![]() необходимо и достаточно, чтобы функция
необходимо и достаточно, чтобы функция
![]() была
ограничена сверху, т.е.
была
ограничена сверху, т.е.
![]() .
.
Доказательство.
Заметим, что если
,
то
–
возрастающая функция. Действительно,
если
![]() ,
то
,
то
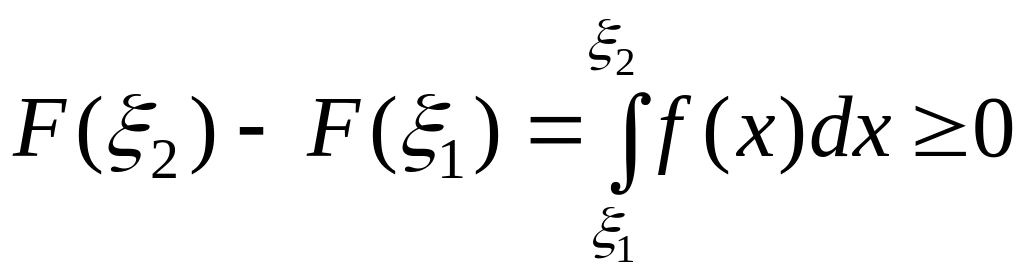 .
Но по критерию существования предела
монотонной функции,
.
Но по критерию существования предела
монотонной функции,
![]() существует тогда, и только тогда, когда
существует тогда, и только тогда, когда
![]() ограничена сверху ■
ограничена сверху ■
Теорема 2
(признак сравнения) Если
выполняется условие
![]() ,
то
,
то
а) из сходимости
интеграла
![]() следует сходимость интеграла
следует сходимость интеграла
![]() ;
б) из расходимости интеграла
следует расходимость интеграла
.
;
б) из расходимости интеграла
следует расходимость интеграла
.
Доказательство.
Так как
,
то, в силу свойств интеграла,
![]() выполняется неравенство:
выполняется неравенство:
![]() .
.
Если интеграл
сходится,
то функция
![]() ограничена сверху, тогда и функция
.
Значит, интеграл
сходится. Если же
расходится, то
не ограничена сверху, тогда и
ограничена сверху, тогда и функция
.
Значит, интеграл
сходится. Если же
расходится, то
не ограничена сверху, тогда и
![]() не ограничена сверху. В силу критерия
сходимости несобственного интеграла
от неотрицательной функции, интеграл
расходится
■
не ограничена сверху. В силу критерия
сходимости несобственного интеграла
от неотрицательной функции, интеграл
расходится
■
Следствие
Если
выполняются условия
![]() ,
,
![]() и при
и при
![]()
![]() ,
то интегралы
,
то интегралы
![]() и
и
![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство.
Так как
при
,
то существует такая окрестность
![]() ,
что
,
что
![]() выполняется
выполняется
![]() ,
т.е.
,
т.е.
![]() .
Отсюда
.
Отсюда
![]() .
.
На отрезке
![]() интегралы
интегралы
![]() и
и
![]() сходятся
как собственные. Значит, сходимость
этих интегралов на
равносильна их сходимости на
сходятся
как собственные. Значит, сходимость
этих интегралов на
равносильна их сходимости на
![]() .
Применяя признак сравнения, из последнего
неравенства получим, что и требовалось
доказать ■
.
Применяя признак сравнения, из последнего
неравенства получим, что и требовалось
доказать ■
Критерий Коши сходимости несобственных интегралов
Для сходимости несобственного интеграла необходимо и достаточно, чтобы выполнялось условие Коши:
![]() .
.
