
Задание 7
Вычислить пределы последовательностей.
Пример 1
![]() .
.
Решение Преобразуем выражение под знаком предела по формулам
![]() ,
,
![]() .
.
Тогда
![]()
![]() [разделим
числитель и знаменатель на
[разделим
числитель и знаменатель на
![]() ]
]![]()
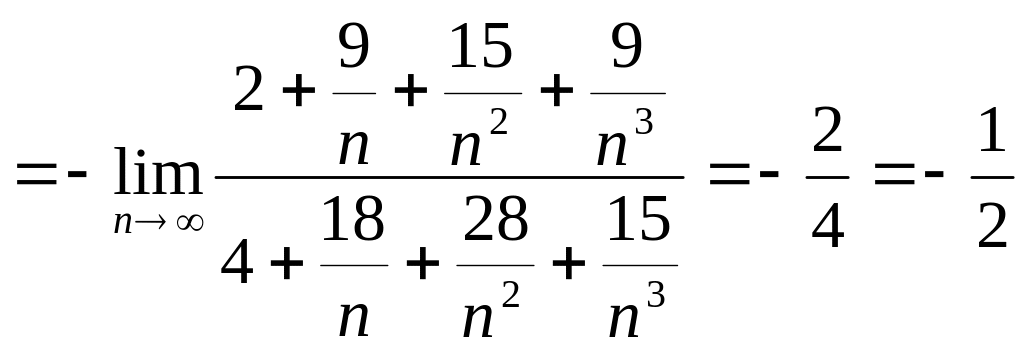 .
.
Здесь мы
воспользовались тем, что
![]() ,
и арифметическими свойствами пределов.
,
и арифметическими свойствами пределов.
Примечание В
дальнейшем при вычислении подобных
пределов можно использовать правило:
при
![]() предел отношения многочленов одинаковых
степеней равен отношению коэффициентов
при старших степенях n.
предел отношения многочленов одинаковых
степеней равен отношению коэффициентов
при старших степенях n.
Пример 2
![]() .
.
Решение Умножим
и разделим выражение под знаком предела
на сопряженное выражение, т. е. на
![]() .
Получим
.
Получим
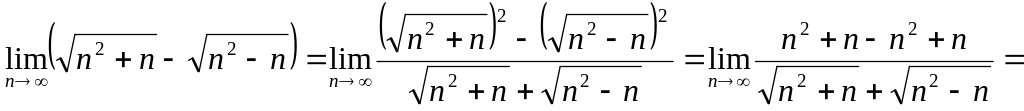
![]() [разделим
числитель и знаменатель на n]
[разделим
числитель и знаменатель на n]
![]() .
.
Пример 3
![]() .
.
Решение Умножим и разделим выражение под знаком предела на неполный квадрат соответствующей суммы, т. е. на
![]() .
.
Получим
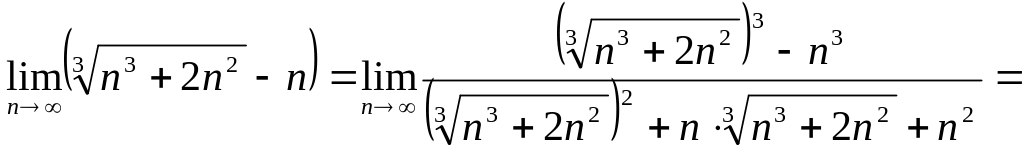
![]() [разделим
числитель и знаменатель на
[разделим
числитель и знаменатель на
![]() ]
]
![]() .
.
Пример 4
![]() .
.
Решение Умножим и разделим выражение под знаком предела на
![]() .
.
Получим
![]()
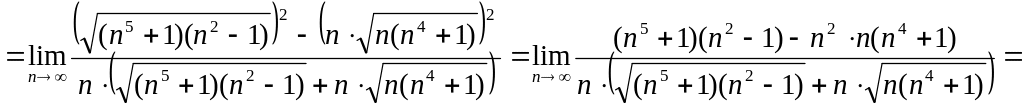
![]()
![]() .
.
Здесь мы воспользовались тем, что старшая степень числителя (5) больше старшей степени знаменателя (4,5).
Пример 5
![]() .
.
Решение Воспользуемся теоремой о промежуточной последовательности и табличными пределами (Приложение А):
![]() ,
,
![]() .
.
Докажем, что данный предел тоже равен 1. Воспользуемся оценками
![]() ,
,
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Пример 6
![]() .
.
Решение Докажем,
что этот предел равен 3. Действительно,
для всех
![]() выполняются неравенства
выполняются неравенства
![]() .
.
Тогда, извлекая корни степени п из всех частей неравенства, получим
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Пример 7
![]() .
.
Решение Заметим,
что для любого натурального
![]()
![]() .
.
Тогда
![]() имеем
имеем
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Задание 8
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Пример 1
![]() .
.
Решение Перейдем
к пределу в числителе и знаменателе.
Получим
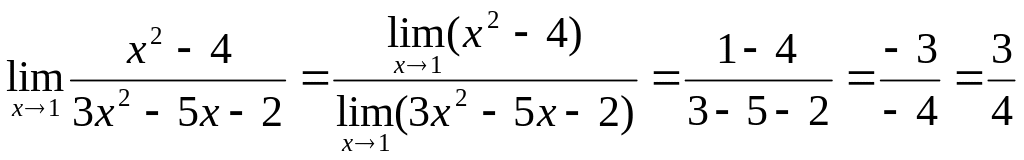 .
.
Пример 2
![]() .
.
Решение
При
![]() и числитель, и знаменатель дроби
стремятся к нулю. Т. е. имеем неопределенность
вида
и числитель, и знаменатель дроби
стремятся к нулю. Т. е. имеем неопределенность
вида
![]() .
Разложим числитель и знаменатель на
множители. Корнями знаменателя являются
.
Разложим числитель и знаменатель на
множители. Корнями знаменателя являются
![]() и
и
![]() .
Поэтому
.
Поэтому
![]() .
.
Пример 3
![]() .
.
Решение Имеем
неопределенность вида
![]() .
Чтобы от нее избавиться, разделим
числитель и знаменатель дроби на х
в старшей
степени, т. е. на
.
Чтобы от нее избавиться, разделим
числитель и знаменатель дроби на х
в старшей
степени, т. е. на
![]() .
Получим
.
Получим
 .
.
Пример 4
![]() .
.
Решение Имеем неопределенность вида . Разложим числитель и знаменатель на множители.
![]()
![]() .
.
Пример 5
![]() .
.
Решение
Имеем неопределенность вида
.
Умножим числитель и знаменатель дроби
на выражения, сопряженные к числителю
и знаменателю, т. е. на
![]() .
Получим
.
Получим
![]()
![]() .
.
Пример 6
![]() .
.
Решение
Имеем неопределенность вида
.
Умножим числитель и знаменатель дроби
на выражения, сопряженные к числителю
и знаменателю, т. е. на
![]() .
.
Получим
![]()
![]()
![]()
Пример 7
![]() .
.
Решение Имеем
неопределенность вида
.
Воспользуемся эквивалентностью функций
при
![]() (Приложение Ам.
зуемся эквивалентностью функций при
(Приложение Ам.
зуемся эквивалентностью функций при
Так как при
![]() и
и
![]() ,
то при
имеем
,
то при
имеем
![]() ,
,
![]() .
.
Тогда
![]() .
.
Пример 8
![]() .
.
Решение
Имеем неопределенность вида
.
Перейдем к новой переменной
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Получим
.
Получим
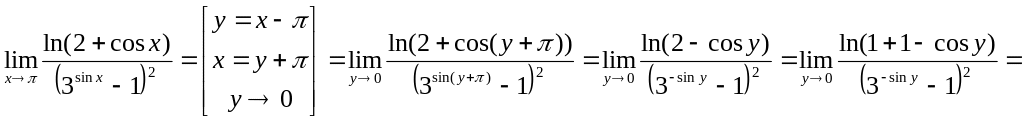
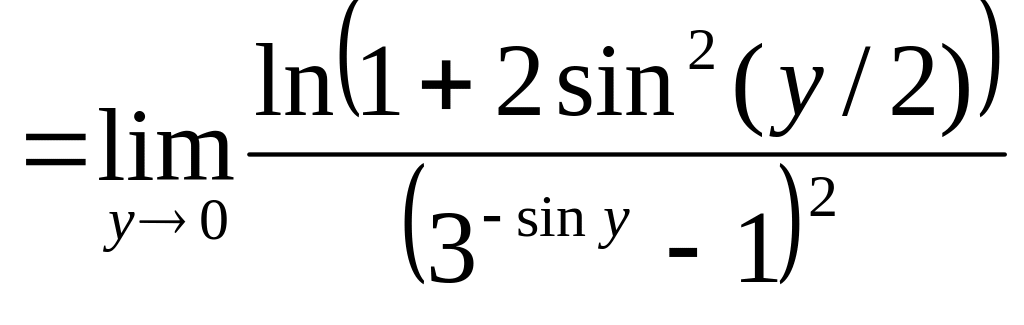 .
.
При
![]() ,
,
![]() .
.
Поэтому последний
предел равен
![]() .
.
