
Задание 9
Найдите односторонние пределы функции
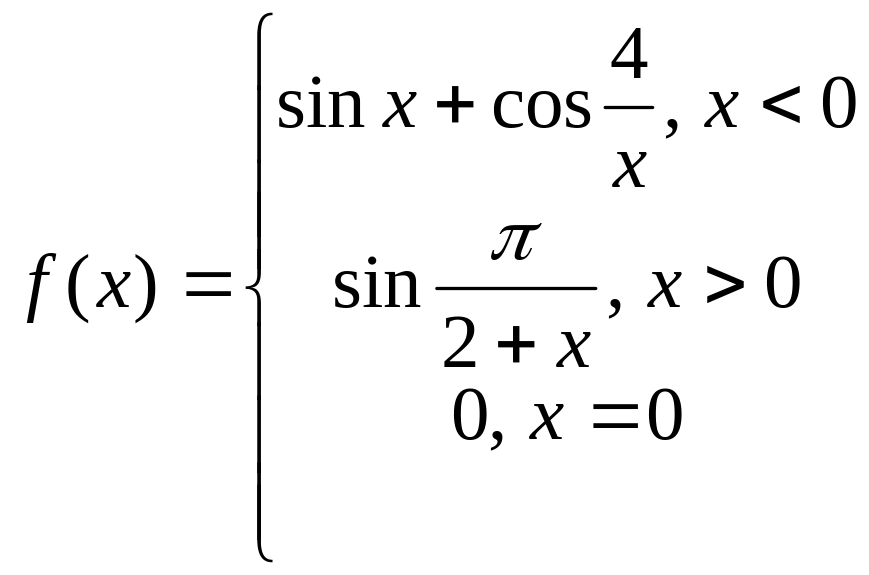 в
точке
в
точке
![]()
или докажите, что соответствующий односторонний предел не существует.
Решение
Правосторонний
предел функции
![]() в точке
существует. Действительно,
в точке
существует. Действительно,
![]() .
.
Покажем, что предела
слева функции
в точке
не существует. В соответствии с
определением по Гейне предела функции
в точке, достаточно указать две
последовательности
,
сходящиеся к нулю слева, такие, что
соответствующие значения функции
![]() будут иметь различные пределы при
.
будут иметь различные пределы при
.
Возьмем
![]() ,
,
![]() .
.
![]() ,
,
![]() при
.
при
.
Возьмем теперь
![]() ,
.
,
.
![]() ,
,
![]() при
при
![]()
Согласно определению
по Гейне предела функции в точке,
![]() не существует.
не существует.
Задание 10
Используя I и II замечательные пределы, вычислить пределы функций.
Пример 1
![]() .
.
Решение Имеем неопределенность вида . Воспользуемся первым замечательным пределом и теоремой о произведении пределов. Получим
![]()
Пример 2
![]() .
.
Решение
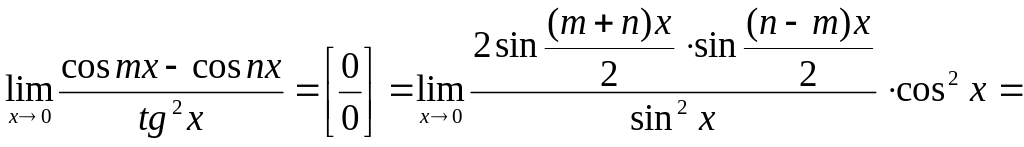
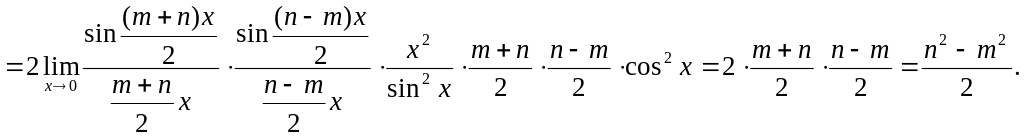
Пример 3
![]() .
.
Решение
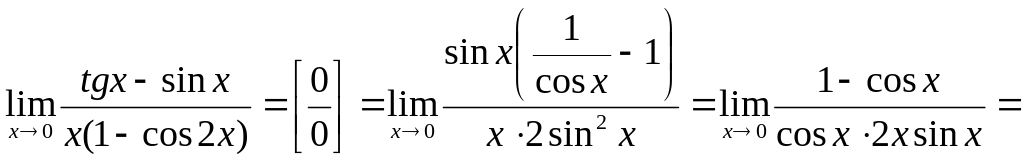
![]()
Пример 4
![]() .
.
Решение Имеем
неопределенность вида
.
Введем новую переменную
![]() ,
тогда
,
тогда
![]() и
и
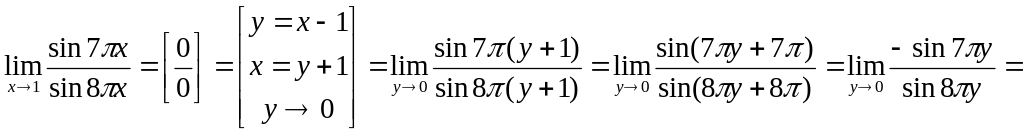
![]() .
.
Пример 5
![]() .
.
Решение
Имеем неопределенность вида [![]() ].
Воспользуемся вторым замечательным
пределом.
].
Воспользуемся вторым замечательным
пределом.
![]()
![]() .
.
Пример 6
![]() .
.
Решение Имеем неопределенность вида [ ]. Воспользуемся вторым замечательным пределом.
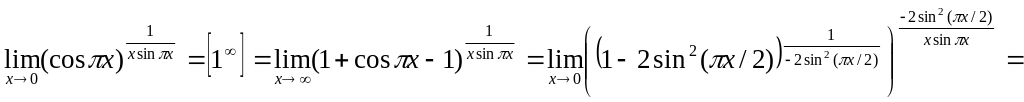
![]() ,
так как
,
так как
![]() .
.
Примечание Использование известных асимптотических равенств несколько упрощает решение задач. Например,
![]() .
.
Пример 7
![]() .
.
Решение Имеем неопределенность вида [ ]. Воспользуемся вторым замечательным пределом.
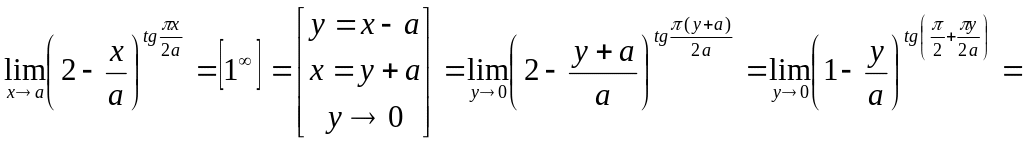
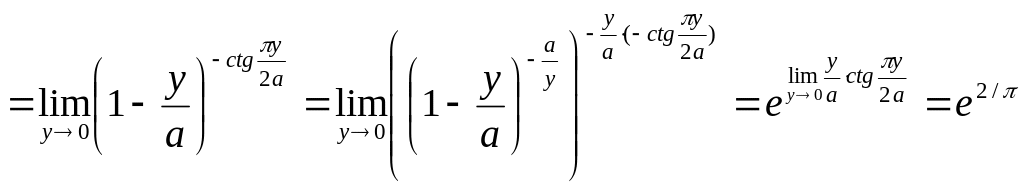 ,
так как
,
так как
![]() .
.
Задание 11
Исследовать данные функции на непрерывность, найти точки разрыва и определить их тип.
Пример 1
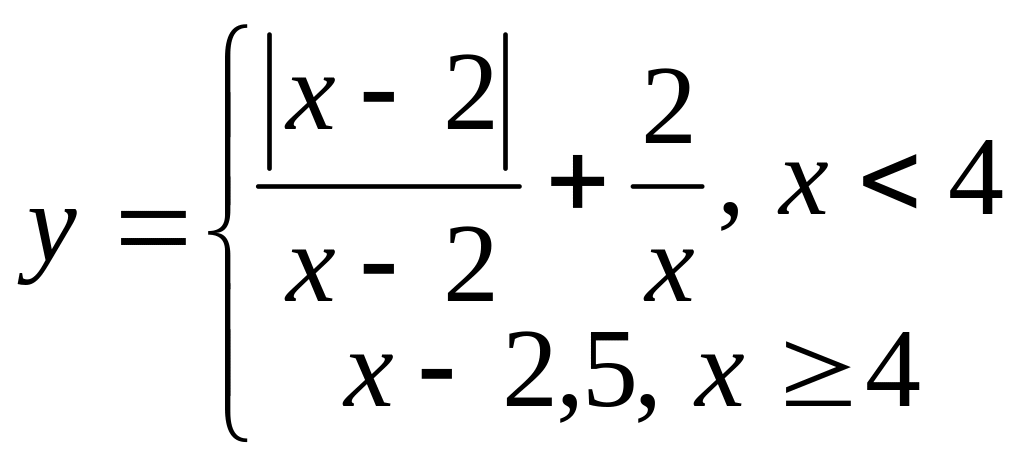 .
.
Решение Так
как
![]() ,
то данную функцию можно записать
следующим образом:
,
то данную функцию можно записать
следующим образом:
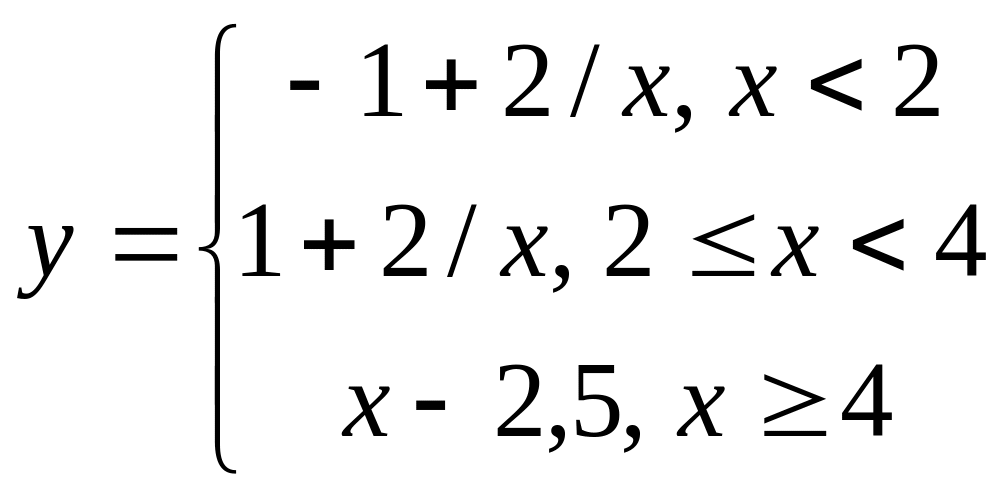 .
.
Данная функция не
определена в точках
и
![]() ,
значит, эти точки являются точками
разрыва. Определим их тип.
,
значит, эти точки являются точками
разрыва. Определим их тип.
Найдем односторонние пределы:
![]() ,
,
![]() .
.
Так как в точке существуют односторонние пределы, но они различны, то – точка разрыва I рода.
Так как
![]() ,
то
– точка разрыва II
рода.
,
то
– точка разрыва II
рода.
Исследуем теперь
функцию на непрерывность в точке
![]() .
.
![]() ,
,
![]() .
.
Поскольку в точке
односторонние пределы существуют и
равны, то существует
![]() и равен 1,5. А так как предел функции
и равен 1,5. А так как предел функции
![]() в точке
совпадает со значением функции в этой
точке, то данная функция непрерывна в
точке
.
в точке
совпадает со значением функции в этой
точке, то данная функция непрерывна в
точке
.
Если
![]() ,
то данная функция непрерывна по
определению непрерывной функции (в
каждой такой точке предел функции
совпадает со значением функции в этой
точке).
,
то данная функция непрерывна по
определению непрерывной функции (в
каждой такой точке предел функции
совпадает со значением функции в этой
точке).
Построим схематически график функции (рисунок 1).
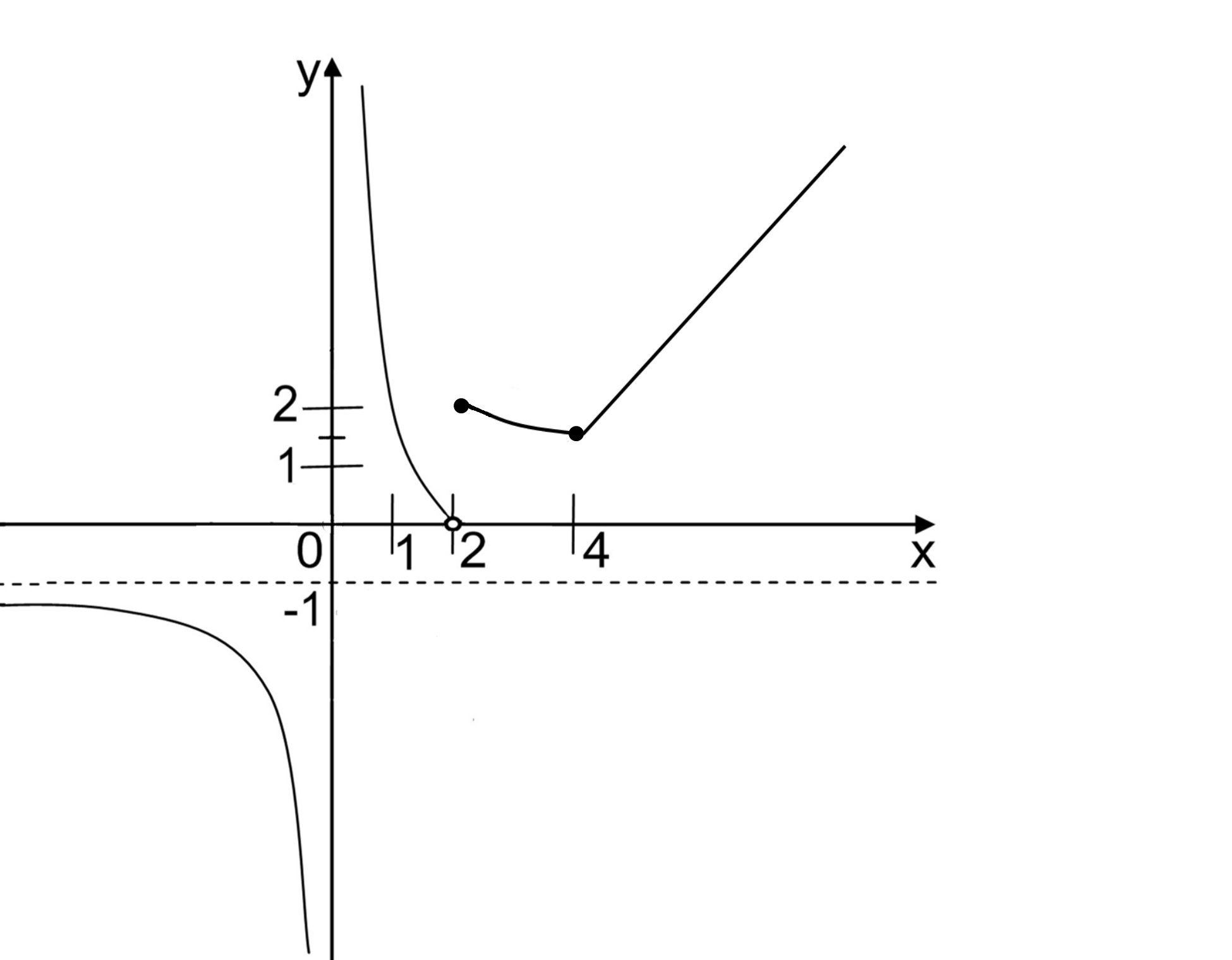
Рисунок 1 − График функции .
Пример 2
![]() .
.
Решение Найдем
точки, в которых знаменатель обращается
в ноль. Решив уравнение
![]() ,
получим
,
получим
![]() ,
,
![]() .
.
Так как функция
не определена в этих точках, то
![]() и
и
![]() – точки разрыва. Определим их тип.
Вычислим пределы функции в этих точках.
– точки разрыва. Определим их тип.
Вычислим пределы функции в этих точках.
![]()
Так как существует конечный предел функции в точке , то – точка устранимого разрыва.
Так как
![]() ,
то
– точка разрыва II
рода.
,
то
– точка разрыва II
рода.
В остальных точках данная функция непрерывна как отношение непрерывных функций.
Пример 3
![]() .
.
Решение Данная функция не определена в точке , значит, она разрывна в этой точке. Рассмотрим ее односторонние пределы в этой точке.
![]() ,
,
![]() .
.
Односторонние пределы существуют, но различны. Значит, – точка разрыва I рода.
Поскольку при
![]() знаменатель
знаменатель
![]() не обращается в ноль, то в остальных
точках данная функция непрерывна как
отношение непрерывных функций.
не обращается в ноль, то в остальных
точках данная функция непрерывна как
отношение непрерывных функций.
Пример 4
![]() .
.
Решение
Данная функция принимает всего три
значения: 0, 1 и –1 – в зависимости от
знака выражения
![]() .
Поэтому запишем ее в следующем виде:
.
Поэтому запишем ее в следующем виде:
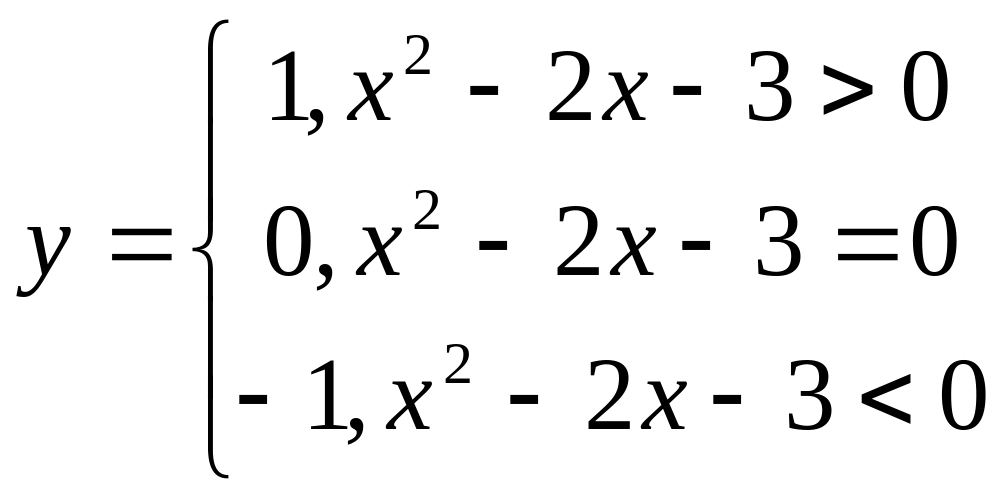 ,
т. е.
,
т. е.
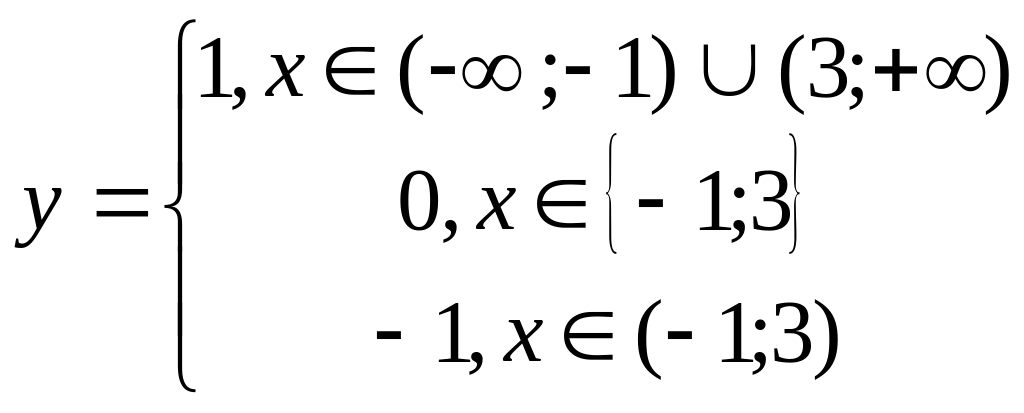 .
.
Рассмотрим, например
точку
![]() (рисунок 2).
(рисунок 2).
![]() ,
,
![]() .
.
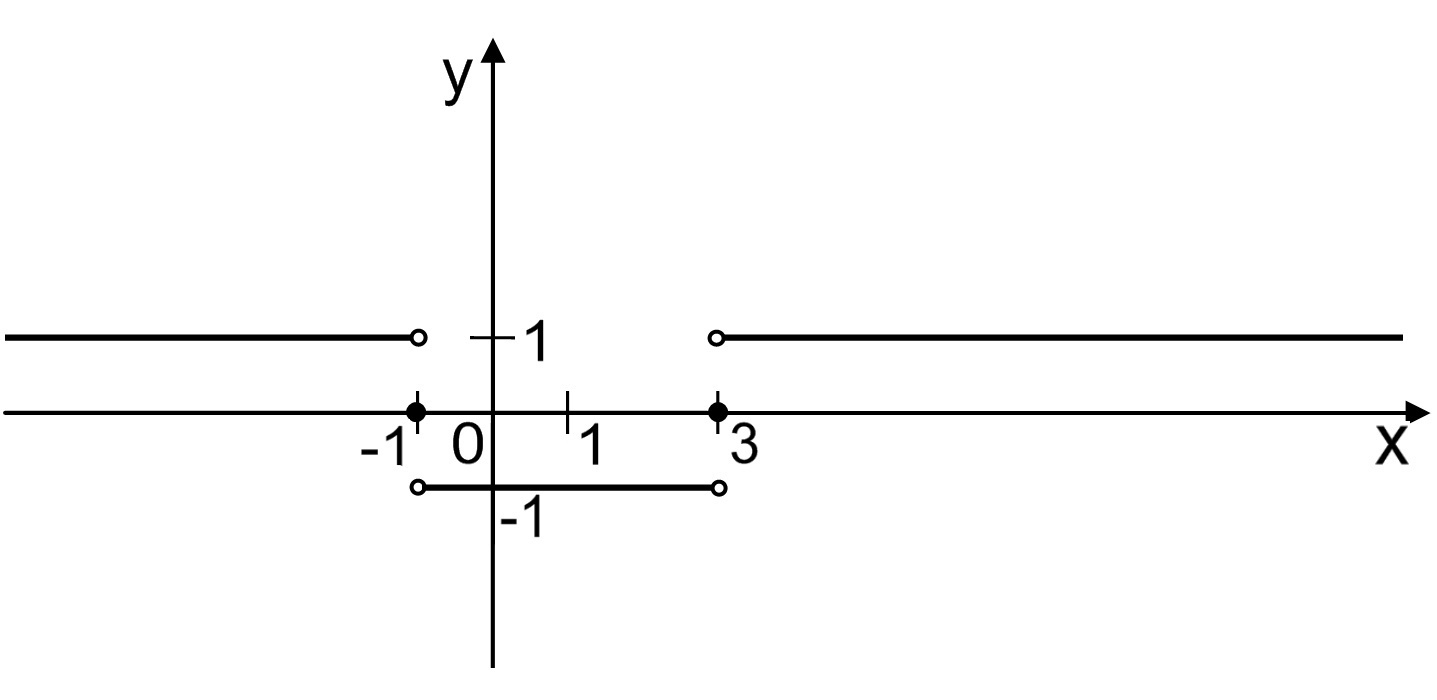
Рисунок 2 − График функции .
Значит, – точка разрыва I рода.
Аналогично
доказывается, что
![]() – тоже точка разрыва I
рода.
– тоже точка разрыва I
рода.
В остальных точках функция является кусочно-постоянной, а значит, непрерывна.
Задание 12
Установить, верно ли утверждение:
![]() при
.
при
.
Решение Воспользуемся леммой:
если
![]() в некоторой проколотой окрестности
точки
в некоторой проколотой окрестности
точки
![]() ,
то
,
то
![]() при
при
![]()
![]()
![]() .
.
Функция
![]() для любого
.
Вычислим
для любого
.
Вычислим
![]() .
.
Заметим, что
величина
![]() является бесконечно малой при
как произведение бесконечно малой
функции
является бесконечно малой при
как произведение бесконечно малой
функции
![]() и ограниченной
и ограниченной
![]() .
Поэтому при
выполняется
.
Поэтому при
выполняется
![]() .
.
Тогда
![]() ,
,
так как
![]() при
,
а
при
,
а
![]() .
.
В силу леммы, данное утверждение верно.
Задание 13
Найти
![]() ,
вычислив
,
вычислив
![]() .
.
Пример 1
![]() .
.
Решение
Преобразуем
![]() .
.
Пусть
![]() .
Выберем
.
Выберем
![]() так, чтобы
так, чтобы
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Получили, что
![]() .
.
При существует только односторонняя производная
![]() .
.
Пример 2
![]() .
.
Решение По
определению производной,
![]() .
.
Воспользуемся
формулой
![]() .
Получим
.
Получим
![]() .
.
Итак,
![]() .
.
Задание 14
Пользуясь
правилами дифференцирования, вычислить
производные данных функций. Записать
дифференциалы
![]() .
.
Пример 1
![]() .
.
Решение Преобразуем выражение, с помощью которого задана функция:
![]() .
.
Воспользуемся формулой производной сложной функции. Получим
![]()
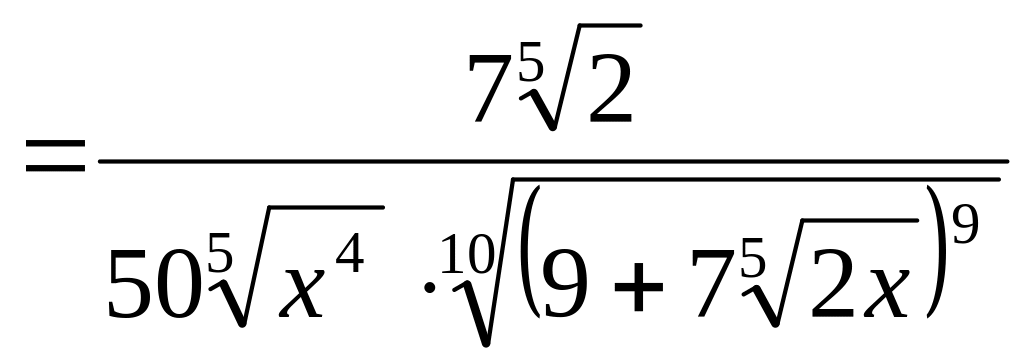 .
.
Дифференциал
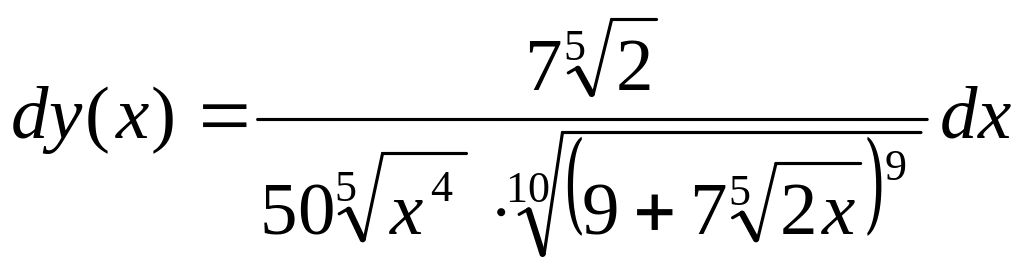 .
.
Пример 2
![]() .
.
Решение Данную функцию можно рассматривать как композицию четырех функций. Применяя правило дифференцирования сложной функции 3 раза, получим
![]() ,
,
![]() .
.
Пример 3
![]() .
.
Решение Воспользуемся правилом дифференцирования произведения:
![]() .
.
Тогда производная
![]()
![]() ,
,
а дифференциал
![]() .
.
Пример 4
![]() .
.
Решение Воспользуемся правилом дифференцирования частного функций:
![]() .
.
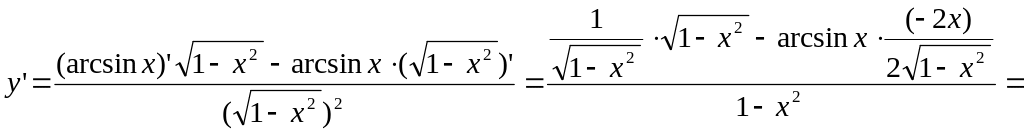
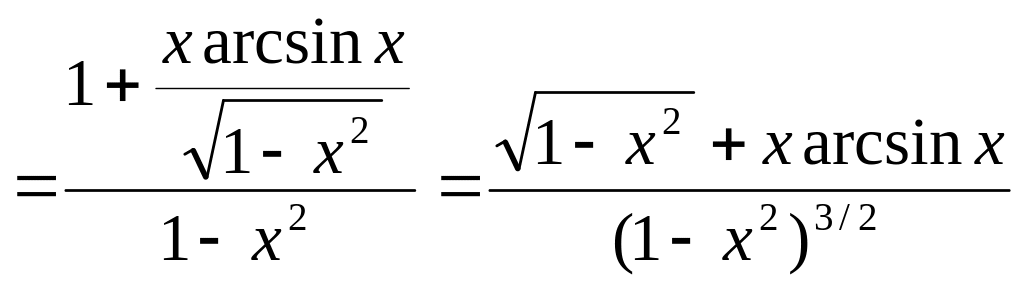 ,
,
дифференциал
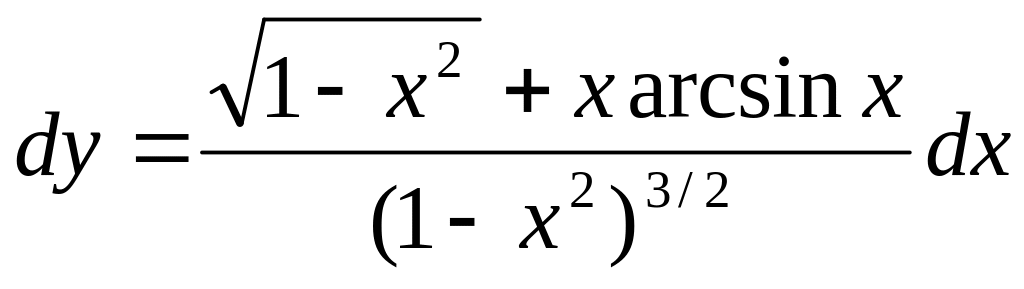 .
.
Пример 5
![]()
![]() .
.
Решение
![]() .
Функция является показательно-степенной.
Для нахождения производной воспользуемся
методом логарифмического дифференцирования.
.
Функция является показательно-степенной.
Для нахождения производной воспользуемся
методом логарифмического дифференцирования.
Прологарифмируем
обе части равенства
![]() .
.
Получим
![]() ,
отсюда
,
отсюда
![]() .
.
Найдем производные от обеих частей последнего равенства, учитывая, что – функция переменной . Воспользовавшись формулами
![]() ,
,
![]() ,
получим
,
получим
![]() .
.
Отсюда
![]() ,
т. е.
,
т. е.
![]() ,
а
,
а
![]() .
.
Пример 6
![]() .
.
Решение Воспользуемся методом логарифмического дифференцирования.
![]()
Воспользовавшись свойствами логарифмов, получим
![]() .
.
Найдем производные от обеих частей последнего равенства, учитывая, что – функция переменной :
![]() .
.
![]()
![]()
![]() .
.
![]() .
.
Задание 15
Найти
![]() для функции, заданной параметрически:
для функции, заданной параметрически:
![]() ,
,![]() .
.
Решение
Воспользуемся формулой производной
функции, заданной параметрически:
![]() .
.
Найдем предварительно
![]() и
и
![]() :
:
![]() ,
,
![]() .
.
Теперь
![]() .
.
Для нахождения
найдем предварительно
![]() .
.
![]() .
.
Теперь
![]() .
.
Примечание Для нахождения можно было воспользоваться формулой:
![]() .
.
Задание 16
Пользуясь правилом Лопиталя, вычислить пределы.
Пример 1
![]() .
.
Решение
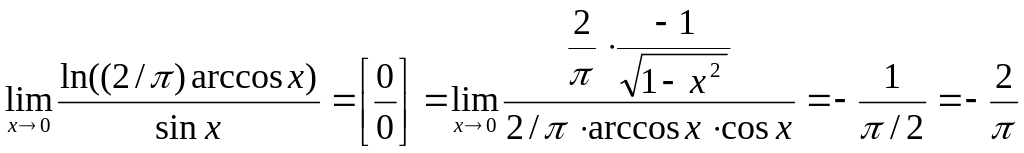 .
.
Пример 2
![]() .
.
Решение
![]() .
.
Пример 3
![]() .
.
Решение Имеем неопределенность вида . Прежде чем применить правило Лопиталя, воспользуемся асимптотическим равенством:
![]() при
.
при
.
Тогда
![]()
![]() .
.
Пример 4
![]() .
.
Решение
![]()
![]() .
.
Пример 5
![]() .
.
Решение
Имеем неопределенность вида
![]() .
Воспользуемся основным логарифмическим
тождеством:
.
Воспользуемся основным логарифмическим
тождеством:
![]() .
.
Тогда
![]() ,
так как
,
так как
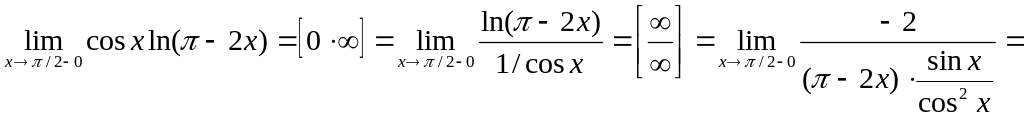
![]() .
.
Задание 17
Пользуясь
основными каноническими разложениями
(Приложение А), разложить по формуле
Маклорена до
![]() следующие функции.
следующие функции.
Пример 1
![]() .
.
Решение
![]()
![]() .
.
Воспользуемся формулой:
![]() .
.
Получим
![]()
![]() .
.
Пример 2
![]() .
.
Решение Применим формулу понижения степени. Получим
![]() .
.
Воспользуемся формулой:
![]() .
.
Тогда
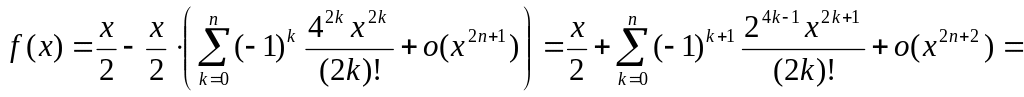
![]() .
.
Пример 3
![]() .
.
Решение
![]() .
.
Представим
![]() в виде
суммы простейших дробей:
в виде
суммы простейших дробей:
![]() .
.
Решив систему
![]() ,
получим
,
получим
![]() ,
,
![]() .
.
Тогда
![]() .
.
Воспользуемся формулами:
![]() ,
,
![]() .
.
Получим
![]()
![]() .
.
Задание 18
Исследовать функцию и построить ее график.
Пример 1
![]() .
.
Решение
1) Область
определения функции
![]() .
.
Так как
![]()
![]() ,
то функция является нечетной. Функция
не является периодической.
,
то функция является нечетной. Функция
не является периодической.
2) Найдем точки пересечения графика функции с осями координат.
С осью
![]() :
:
![]() .
Тогда
.
Тогда
![]() .
Отсюда
.
.
Отсюда
.
С осью
![]() :
.
Тогда
.
Получили точку
:
.
Тогда
.
Получили точку
![]() .
.
Найдем промежутки
знакопостоянства, решив неравенства
![]() и
и
![]() .
Получим:
.
Получим:
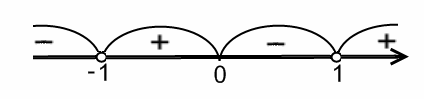
при
![]() ,
,
при
![]() .
.
3) Найдем асимптоты графика функции.
Так как
![]() и
и
![]() ,
то прямые
,
то прямые
![]() и
– вертикальные асимптоты.
и
– вертикальные асимптоты.
![]() ,
,
![]() .
.
Примечание При построении графика функции можно использовать его симметрию относительно начала координат, поэтому односторонние пределы достаточно вычислить только в точке .
Так как
![]() ,
а
,
а
![]() ,
то наклонных и горизонтальных асимптот
нет.
,
то наклонных и горизонтальных асимптот
нет.
4) Исследуем функцию на монотонность и найдем точки экстремума. Для этого вычислим производную функции:
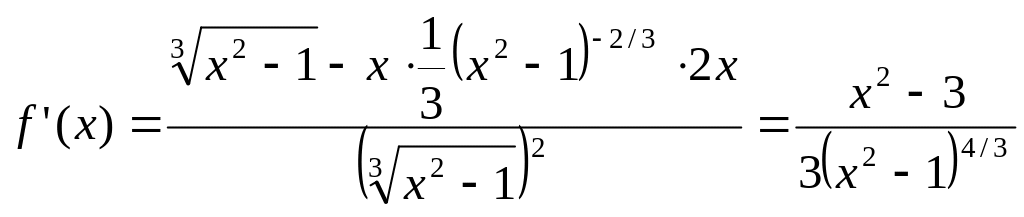 .
.
![]() ,
если
,
если
![]() .
.
Исследуем знак . Получим:

возрастает на
![]() и
и
![]() ,
,
убывает на
![]() ,
,
![]() и на
и на
![]() .
.
![]() – точка максимума,
– точка максимума,
![]() – точка минимума.
– точка минимума.
![]() .
.
5) Найдем промежутки выпуклости и точки перегиба.
 .
.
![]() ,
если
или
,
если
или
![]() .
.
Исследуем знак
![]() .
Получим:
.
Получим:
![]()
выпукла вниз на
![]() ,
,![]() ,
,![]() ,
,
выпукла вверх на
![]() ,
,![]() ,
,![]() .
.
и
– точки перегиба,
![]() ,
,
![]() .
.
6) Изобразим график данной функции (рисунок 3).
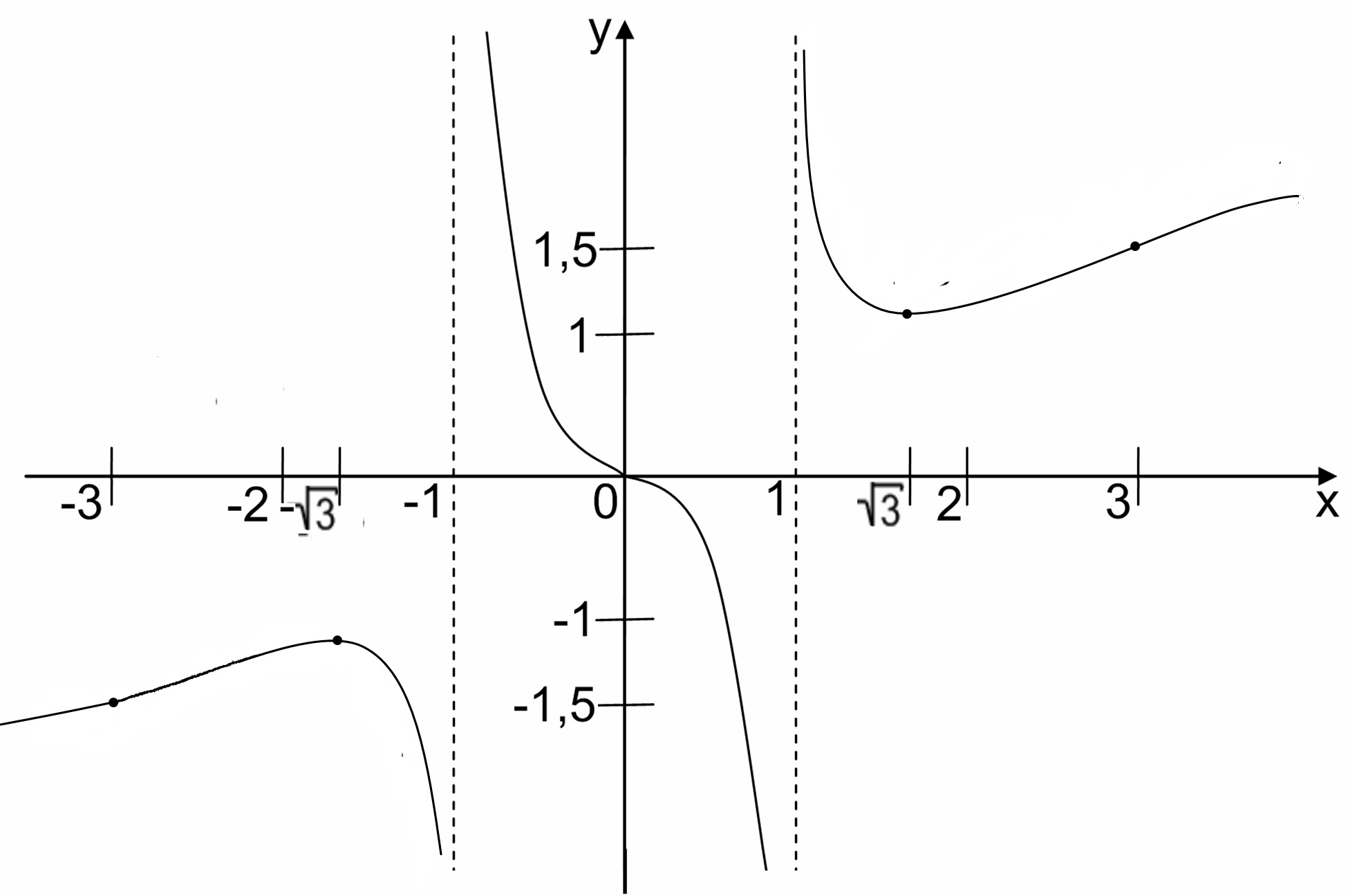
Рисунок 3 − График функции .
Пример 2
![]() .
.
Решение
1) Найдем область определения:
и
![]() ,
т.е.
,
т.е.
![]() .
.
Получили
![]() .
.
Так как область определения не симметрична относительно начала координат, то не является ни четной, ни нечетной. Не является периодической.
2) Найдем точки пересечения графика функции с осями координат.
С осью
:
,
т. е.
![]() .
Уравнение не имеет корней.
.
Уравнение не имеет корней.
С осью
:
.
Но
![]() .
.
Значит, точек пересечения с осями координат нет.
Найдем промежутки знакопостоянства. Получим:
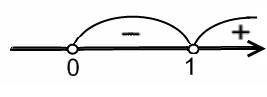
при
![]() ,
при
,
при
![]() .
.
3) Для нахождения вертикальных асимптот исследуем поведение функции в точках или .
![]() ,
,
![]() .
.
Значит, прямая является вертикальной асимптотой.
4) Найдем промежутки монотонности и точки экстремума.
![]() .
.
,
если
![]() ,
,
![]() .
.
Исследуем знак . Получим:
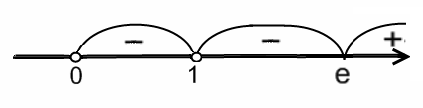
возрастает на
![]() ,
,
убывает на
![]() и
и
![]() .
.
– точка минимума,
![]() .
.
5) Найдем промежутки выпуклости и точки перегиба.
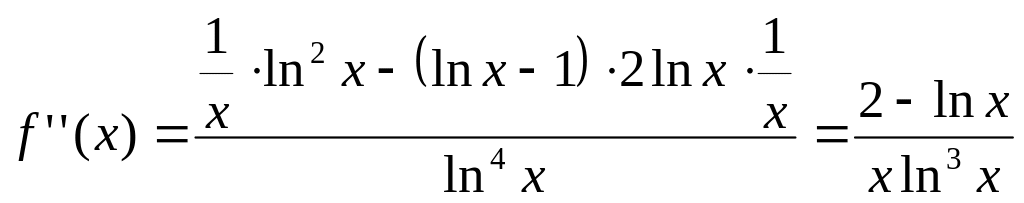 .
.
,
если
![]() ,
,
![]() .
.
Исследуем знак . Получим:
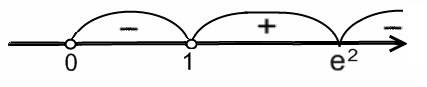
выпукла вверх на
и
![]() ,
,
выпукла вниз на
![]() .
.
– точка перегиба,
![]() .
.
6) Изобразим график данной функции (рисунок 4).
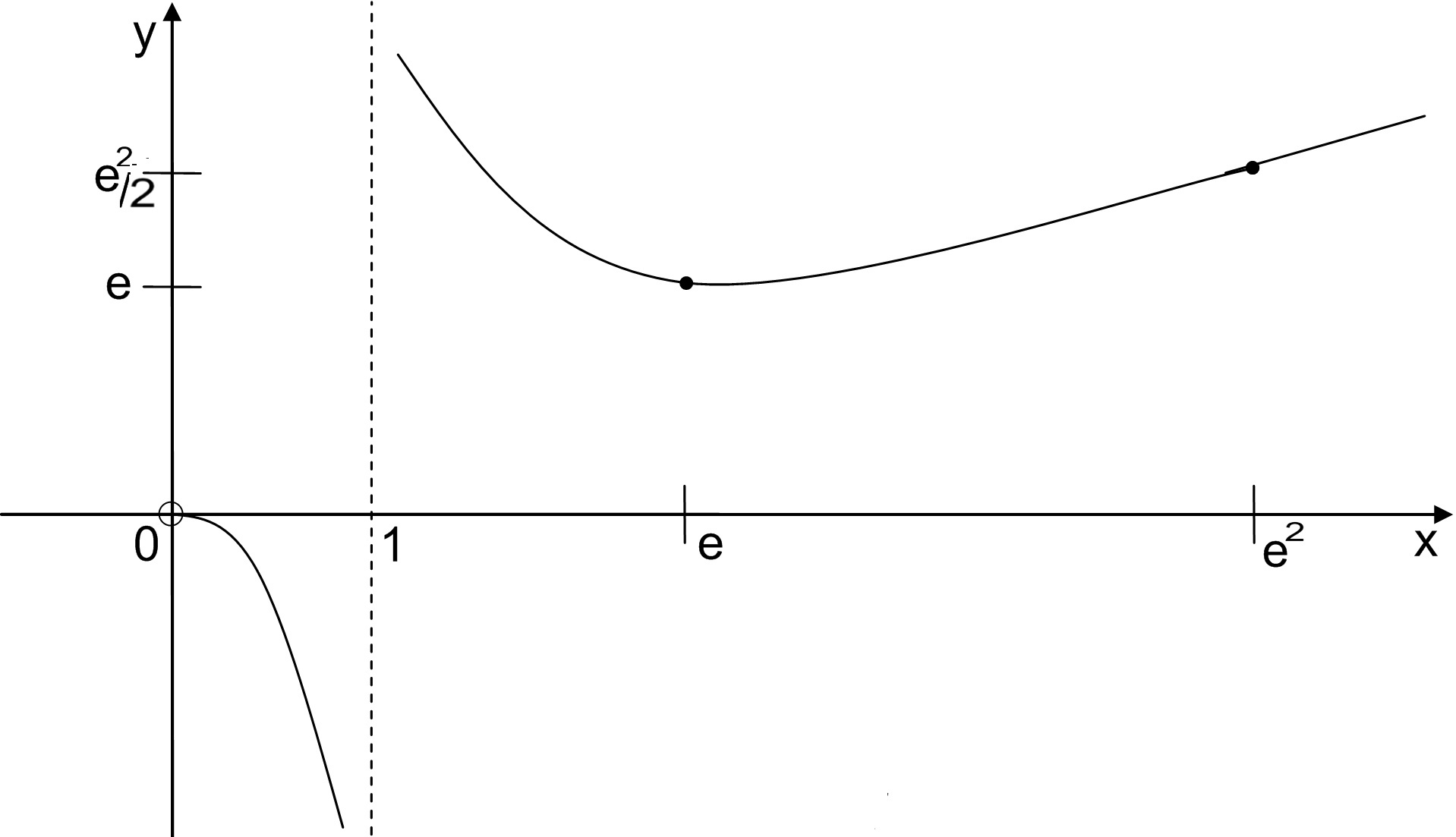
Рисунок 4 − График функции .
