- •Содержание Оптические инструменты для визуального контроля Введение
- •Глава 1. Оптические инструменты, вооружающие глаз.
- •Глава 2. Дифракционные явления в оптических инструментах.
- •Введение
- •Глава 1. Оптические инструменты, вооружающие глаз.
- •1.1. Оптические приборы для визуальных наблюдений
- •1.2. Оптические инструменты :
- •1.2.1. Лупа.
- •1.2.2. Микроскоп
- •Принципиальная схема микроскопа и осветительной системы
- •1.2.2.1. Глубина резкости
- •1.2.2.2.Освещение предмета в микроскопе
- •1.2.2.3.Маркировка объективов для микроскопов.
- •1.2.2.4.Классификация объективов по степени исправления искажений:
- •1.2.3. Зрительная труба; Телескоп.
- •1.2.3.1.Формулы для телескопа
- •1.2.3.3.Крупнейшие рефракторы
- •1.2.4. Проекционные аппараты.
- •1.2.5. Спектроскоп
- •Глава 2. Дифракционные явления в оптических инструментах
- •2.1. Дифракция Фраунгофера в геометрически сопряженных плоскостях.
- •2.2. Дифракция Фраунгофера на щели и круглом отверстии.
- •2.2.1. Дифракция на щели
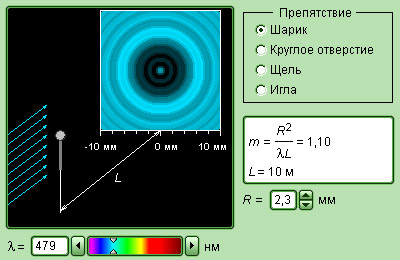
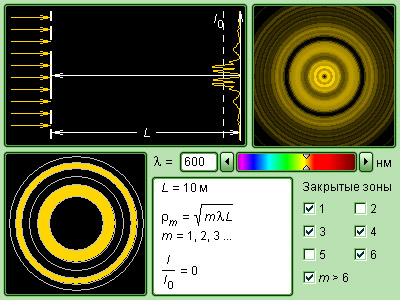
- •2.2.2.Дифракция света на круглом отверстии
- •2.2.3. Расчет радиусов Френеля при сферическом волновом фронте
- •2.3. Интенсивность света в фокусе линзы.
- •2.4. Дифракционный предел разрешения оптических инструментов
- •2.4.1.. Разрешающая способность телескопа.
- •2.4.1.1. Поправки,вносимые дифракционной теорией в геометрическую теорию изображения
- •140/ D (секунд дуги),
- •2.4.2. Разрешающая способность глаза.
- •2.4.3. Предел разрешения микроскопа
- •2.4.4. Замечание о нормальном увеличении оптических инструментов.
- •Заключение
- •Содержание контрольных вопросов.
- •Предел разрешения микроскопа.
- •Примерные задания для курсовой работы.
2.2.3. Расчет радиусов Френеля при сферическом волновом фронте
Пусть S - источник волн, а M - точка наблюдения. Отметим на волновой сферической поверхности точки, соответствующие границам m-ой зоны Френеля. Эти точки находятся на расстоянии L + m λ/2 от
точки М. Радиус m- -ой зоны равен ri = AB, OB = h m - высота сегмента (рис. 2.10.) Рассмотрим ∆ SAB и ∆ ABM. Из треугольника ASB
ri 2=R 2-(R-h m )2=2Rh m -h m 2. (11
Из треугольника A M B имеем
ri 2 =(L + m λ/2)2 -(L+hi )2 = m λ L-2Lhi . (12

Рис. 2.10
Члены hi 2 и m2 (λ /2) 2 отбросим как величины, имеющие второй порядок малости. Из (12) найдем:
ri=(2 Rhi.)1/ 2 (13)
Приравняв правые части (11) и (12), получим: hi= m λ L/2(R + L)
Подставим (14) в (13), найдем радиус m -ой зоны Френеля для сферического фронта
ri=![]() (
(![]() L
R
/
R
+
L)
L
R
/
R
+
L)![]() m
λ.В (15)
m
λ.В (15)
Радиус первой зоны при m = 1 равен r1 = r = ( L R / R + L)х λ. Тогда радиус m -ой зоны равен
r m=( mr 1. (16)
Следовательно, для радиусов зон справедливо соотношение: r 1: r2: r 3... = 1: 2: 3
Найдем радиусы зон Френеля для плоского волнового фронта. Запишем выражение (15) в виде
r
1i=
iLλ
![]() 1+
L/
R
1+
L/
R
Для
плоского фронта R
-![]()
![]()
![]() .
Тогда получим
.
Тогда получим
r 1i= (mLλ). (17)
(18)
Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.
Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т. Юнг, О. Френель и другие ученые развивали волновые представления, еще не была известна.
|
Модель. Дифракция света |
|
Модель. Зоны Френеля |
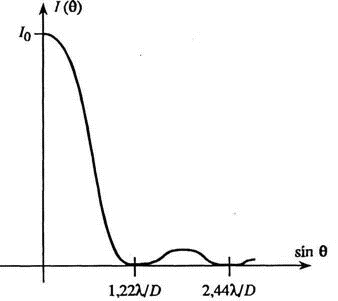
Расчет фраунгоферовой дифракции на круглом отверстии оказывается достаточно громоздким и приводит к бесселевым функциям первого порядка I1.
Распределение интенсивности света при дифракции Фраунгофера на круглом
отверстии диаметра D выражается формулой
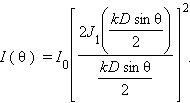 (2.3)
(2.3)
К=2π/λ , D—диметр объектива, θ - угол наблюдения, sin θ =m λ/D
Ĵ1(х) – Функция Бесселя 1 – ого рода, имеющая корни
Ĵ1(х) = 0 при х1 = 3.84 ; х2= 7.04; х3 = 10.18
При
θ
→
0
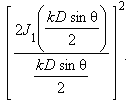 →
1 , тогда
І (0)
= І0
→
1 , тогда
І (0)
= І0
При ( k D Sin θ) /2 =3.84, тогда из этого соотношения ,учитывая,что
К=2π/ λ
Sin θ = ( 2 3.84 λ) / 2π D при малых углах θ
Δ θ =1.22 λ/D
Рис. 2.13. Дифракция Фраунгофера на круглом отверстии
Распределения (2.2) и (2.3) очень похожи друг на друга. Картина дифракции на круглом отверстии имеет вид концентрических колец. Центральное светлое пятно носит название пятна Эйри. Интенсивность в максимуме первого светлого кольца составляет приблизительно 2 % от интенсивности в центре пятна Эйри. Распределение (2.3) показано на рис.2.13.
При оценке разрешающей способности оптических инструментов важно знать размер центрального дифракционного максимума. Угловой радиус пятна Эйри выражается соотношением
![]() (2.4)
(2.4)