http://model.exponenta.ru/bt/bt_00111.html Федосов Борис Трофимович

Экспресс-анализ сар по ее передаточной функции

Для линейных систем, не содержащих элементов запаздывания, передаточная функция является дробно-рациональной, т.е. имеет вид дроби, в числителе и знаменателе которой записаны полиномы от переменной p в русской технической литературе или s в английской. В общем виде передаточную функцию записывают так:

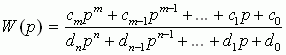
(2)

Инженерам же удобнее применять форму, которую можно назвать канонической, когда свободные члены полиномов, как числителя, так и знаменателя равны единице:

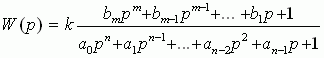
(3)

Это позволяет при анализе свойств системы без выполнения каких-либо сложных математических действий сразу получать важные сведения о системе, в частности, реализуема ли она. Условие физической реализации: степень числителя m должна быть меньше степени знаменателя n (m < n).

Для приведения (2) к виду (3) достаточно в числителе и знаменателе вынести c₀ и d₀ соответственно за скобки и разделить c₀ на d₀, что даст величину k. В большинстве практически значимых случаев система содержит не более одного – двух форсирующих звеньев, поэтому передаточную функцию можно и целесообразно представить в виде:

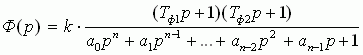
(4)

Для разложения числителя (3) на простые множители при m = 2 потребуется решить квадратное уравнение.

При анализе линейной системы в первую очередь интересно знать, устойчива ли она, а на следующем этапе определяется качество САР в статике, переходном и установившемся режимах. Качество может характеризоваться как прямыми, так и косвенными параметрами.

2. Характеристики и свойства линейной системы, лежащие на поверхности

2.1. Оценка свойств системы по передаточной функции ее замкнутого контура

Главные вопросы при анализе свойств САР – ее работоспособность и качество. Если рассматриваемая система заведомо устойчива, а значит, в принципе работоспособна, то можно заняться изучением непосредственно параметров ее качества. Но если не известно, устойчива ли САР, то оценить степень ее устойчивости с высокой степенью вероятности без сложных вычислений могут помочь следующие правила.

2.1.1.Устойчивость

Передаточная функция Ф(p) замкнутой САР позволяет охарактеризовать все свойства исследуемой линейной системы. В первую очередь необходимо установить, устойчива ли САР. Ответ на этот вопрос дает применение критериев устойчивости, но они требуют выполнения некоторых действий, в том числе и в программах моделирования. Наряду с классическими критериями устойчивости желательно было бы иметь достаточно простые в применении правила, позволяющие судить об устойчивости на вскидку, путем сравнения самих коэффициентов характеристического полинома или, по крайней мере, простых арифметических выражений, составленных из них.

К сожалению, в литературе не встречается рекомендаций на эту тему, за исключением систем первого, второго и третьего порядков, для которых простые правила даются критерием устойчивости Гурвица. Поэтому оценка устойчивости системы на вскидку по ее характеристическому полиному требует привлечения инженерной интуиции. Тем не менее, здесь могут быть даны некоторые рекомендации, упрощающие эту работу.

Пусть передаточная функция Ф(p) замкнутой САР имеет вид:

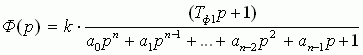
(5)

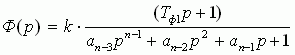1. В первую очередь целесообразно посмотреть, устойчива ли низкочастотная часть исходной САР. Для этого рассматривается усеченная передаточная функция:

(6)

Примечание ВЕК. В приведенной формуле, вероятно, описка: необходимо заменить p^n-1на p³.

(6)

Здесь, в соответствии с критерием Гурвица для устойчивости необходимо и достаточно, чтобы a_n-3<a_n-2*a_n-1 , что легко проверяется в уме или на калькуляторе. Оптимизма прибавится, если НЧ часть будет иметь хороший запас устойчивости, когда левая часть неравенства будет в несколько (много) раз меньшей, чем правая.

2. Коэффициенты полинома a_n-3, a_n-2 и a_n-1 у устойчивой системы могут быть разными, они могут возрастать или убывать с понижением индекса. Коэффициенты полинома, начиная с a_n-3, у устойчивой системы убывают все быстрее с уменьшением индекса.

Практическую верхнюю границу скорости убывания при которой система скорее всего устойчива, можно, например, задать системой неравенств:

a_k-3.a_k < a_k-2.a_k-1