18.2. Формирование множества критериев

Количество критериев должно охватывать все особенности задачи. Число критериев считается полным и достаточным, если прибавление нового критерия не изменит результата решения, а отбрасывание критерия этот результат меняет. Все критерии не должны сильно коррелировать друг с другом. Степень корреляции между μ и ν критериями можно определить по следующей формуле:

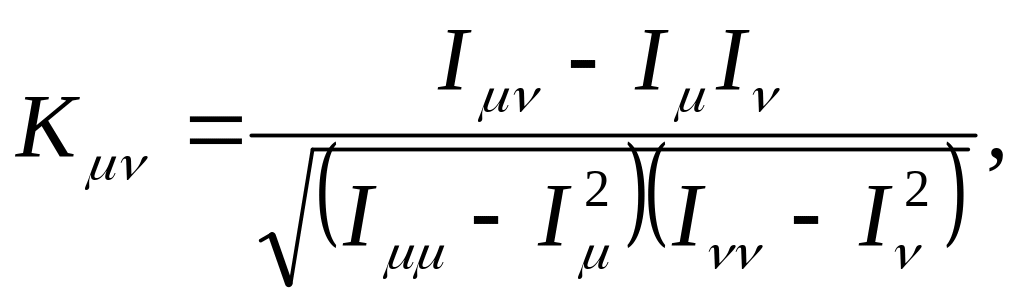
где

где Хi – случайная альтернатива из множества , i=1, …, N; fμ(Хi), fν(Хi) – критерии; N – число случайных испытаний.

Если K приближается к 1, то это свидетельствует о сильной корреляции критериев. Тогда необходимо рассмотреть вопрос об исключении одного из критериев.

Каждому критерию может быть поставлена в соответствие своя координатная ось и шкала. Последняя может быть непрерывной или дискретной, количественной или качественной (рис. 4).

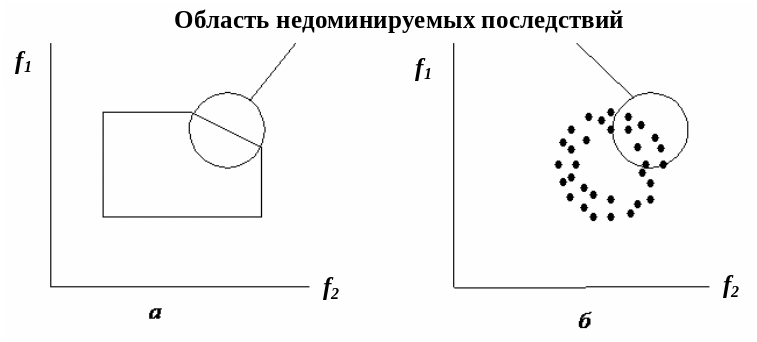
Рис. 4. Выбор альтернативы с учетом двух критериев: а — в случае непрерывной области альтернатив; б — в случае дискретных альтернатив

Каждую ось будем обозначать буквой fk, k = 1, 2, …, r. f1 × f2 × ... × fr – декартово произведение, которое формирует пространство критериев, где имеет место множество векторных оценок. Между пространством параметров и пространством критериев существует соответствие (рис. 5).

Рис. 5. Пространства параметров и критериев:

D – допустимая область, DФ – аналог допустимой области в пространстве критериев

18.3 Методология решения многокритериальных задач

При решении многокритериальных задач обычно задаются параметрические ограничения вида xi min ≤ xi ≤ xi mах, при i=1, 2, …, n, которые формируют в пространстве параметров n-мерный параллелепипед (рис. 4, а). Далее предполагается, что заданы функциональные ограничения вида pj (x) ≤ 0, при j=1, 2, …, m, которые вырезают в параллелепипеде некоторую часть D, состоящую из точек Х, удовлетворяющих одновременно параметрическим и функциональным ограничениям. В лекции 5 эту часть пространства мы называли допустимой областью (ДО). Множество D может оказаться весьма сложным, например, состоящим из нескольких отдельных частей (рис. 6, б, закрашенные участки).

Наконец, предполагается, что заданы соответствующие критерии fk(Хi), k =1, 2, …, r. Для определенности здесь будем считать, что критерии f1, …, fr желательно уменьшить.

Предположим, что ЛПР сумел указать разумные критериальные ограничения вида , при k =1, 2, …, r. При этом – значение для одной из линий равного уровня n-го критерия.

Очевидно, – это наихудшее значение критерия, на которое ЛПР может согласиться. Обозначим через G множество точек Х, которые удовлетворяют параметрическим, функциональным и критериальным ограничениям. Понятно, что (рис. 6, в, закрашенные области).

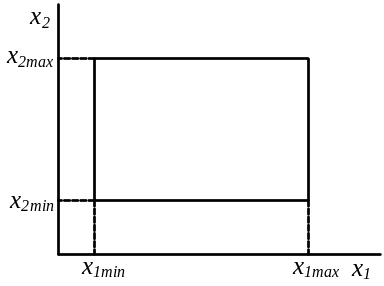
а)

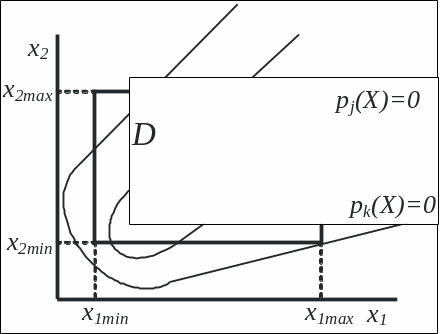
б)

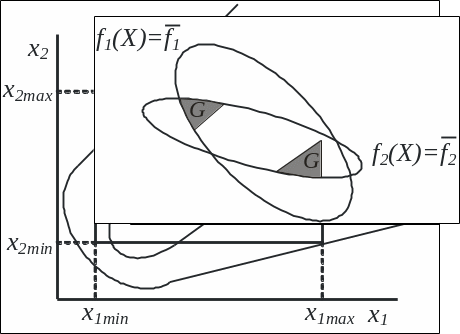
в)

Рис. 6. Формирование параметрическими (а), функциональными (б) и критериальными (в) ограничениями области поиска экстремума

Наилучшее решение целесообразнее искать среди точек множества G, а не среди точек множества D, поскольку, если точка , то значения всех критериев в этой точке приемлемы. Понятно, что завышенные требования ЛПР могут привести к G=0, т.е. область поиска решений окажется пустой.

При решении многокритериальных задач выбора основная трудность состоит в неоднозначности выбора наилучшего решения. Для ее преодоления используют две группы методов.

В методах первой группы стремятся сократить число критериев, для чего вводят дополнительные предположения, относящиеся к процедуре сопоставления критериев и построению моделей оптимизации. В методах первой группы стремятся сократить число альтернатив в исходном множестве, исключив заведомо плохие альтернативы.

К методам первой группы относятся метод свертки, метод главного критерия, метод пороговых критериев и метод расстояния.

Методы второй группы основаны на свертке в множестве альтернатив. С их помощью пытаются уменьшить число возможных вариантов решений, исключив заведомо плохие. Один из подходов, обладающий большой общностью, называется методом, основанным на принципе Парето. Для уменьшение числа альтернатив исходного множества выделяют множество Парето, являющееся подмножеством исходного.

После того, как построено множество Парето, для определения наилучшего решения (из оставшихся) применяются методы первой группы либо графические методы, например, метод диаграмм. Схема поиска наилучшего решения представлена на рис. 7.

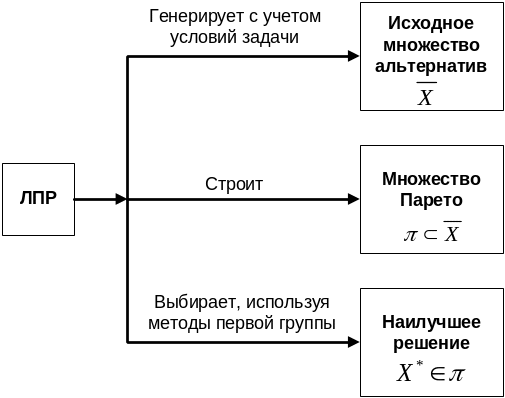
Рис. 7. Схема поиска наилучшего решения

Подчас необходимые для определения предпочтений знания в области ТПР, умения и навыки у ЛПР отсутствуют, а требуемые для совершения этой работы активные ресурсы – время, деньги, специальное математическое обеспечение и т. п. – отсутствуют в нужных количествах. Да ведь и не все проблемы, возникающие перед ЛПР, на практике оказываются столь важными, чтобы обязательно и как можно более точно моделировать его предпочтения. Как тут быть? Во всех перечисленных случаях для отыскания, наилучшей альтернативы ТПР рекомендует ЛПР следовать принципу Родена. Когда у этого великого скульптора спросили, как ему удается создавать столь великие шедевры, Роден ответил: «Я просто беру глыбу мрамора и отсекаю от нее все лишнее!».

Прекрасная идея: последовательно отсекайте от множества альтернатив все элементы, которые «не нужны», которые являются «лишними», а то, что останется (не лишнее) – это и есть то, что вам нужно – наилучшая альтернатива (или несколько эквивалентных по предпочтительности наилучших альтернатив). Концептуальную идею, изложенную в вербальной форме Роденом, реализовал в формальном виде и превратил в одну из наиболее эффективных функций выбора видный социолог и итальянский экономист Вильфредо Парето в 1897 году.

Он рассматривал распределение богатства и доходов в Англии XIX века. Он выяснил, что большая часть доходов и материальных ценностей принадлежит меньшинству людей в исследованных группах. Возможно, что для Парето не было в этом ничего удивительного. Однако он также установил два очень примечательных, по его мнению, факта. Первым был тот, что существует неизменное математическое соотношение между численностью группы людей (в процентах от общей численности рассматриваемого населения) и долей богатства или дохода, контролируемой этой группой. Другими словами, если известно, что 20% населения владеют 80% материальных ценностей, то можно с уверенностью сказать, что 10% населения имеют приблизительно 65% материальных ценностей, а 5% населения — 50%. Для Парето главным здесь были не цифры процентного соотношения, а тот факт, что распределение богатства среди населения предсказуемо несбалансированно.

Другой находкой Парето, восхитившей его, было то, что данная схема дисбаланса оставалась неизменной для статистических данных, относящихся к различным периодам времени и различным странам. Будь то данные по Англии за любой период ее истории или доступные Парето данные по другим странам за разные периоды времени, выяснялось, что схема снова и снова повторяется, причем с математической точностью.

Его открытие называли по-разному, в том числе принципом Парето, законом Парето, правилом 80/20, принципом наименьшего усилия, принципом Дисбаланса.

Принцип 80/20 гласит, что небольшая доля причин, вкладываемых средств или прилагаемых усилий, отвечает за большую долю результатов, получаемой продукции или заработанного вознаграждения. Например, на получение 80% результатов, достигаемых в работе, у вас уходит 20% всего затраченного времени. Выходит, что на практике 4/5 приложенных вами усилий (немалая доля) не имеют к получаемому результату почти никакого отношения. Это, кстати, расходится с тем, чего люди обычно ожидают.

Введем на множестве D отношение предпочтения (обозначим его символом ). Будем говорить, что вектор предпочтительнее вектора , и писать , если среди равенств и неравенств имеется хотя бы одно строгое неравенство (рис. 6).

Аналогично на множестве DФ введем отношение доминирования: будем говорить, что векторный критерий оптимальности доминирует векторный критерий оптимальности , и писать , если .

Другими словами, объект доминирует объект , если по всем критериям предпочтительнее или эквивалентен , и хотя бы по одному критерию строго предпочтительнее. Объект называют доминирующим, а – доминируемым.

Если исключить из исходного множества доминируемые объекты, то останутся конкурирующие (эффективные).

Введенные отношение предпочтения и отношение доминирования являются транзитивными, т.е.

если и , то ;

если и , то

Выделим из множества DФ подмножество точек, для которых нет точек, их доминирующих. Множество , соответствующее , называется множеством Парето (переговорным множеством, областью компромисса) — рис. 7. Поскольку множество DФ на рисунке 7 является выпуклым, то множество  есть часть границы множества DФ — дуга AB, в которой точка A соответствует f1min, а точка B  f2min. Среди точек

,

нет более предпочтительных, поскольку

, но .

Таким образом, если , то .

Другими словами множество Парето можно определить как множество, в котором значение любого из скалярных (частных) критериев оптимальности можно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям.

Альтернатива принадлежит множеству Парето, если она не хуже других по всем критериям и хотя бы по одному критерию лучше.

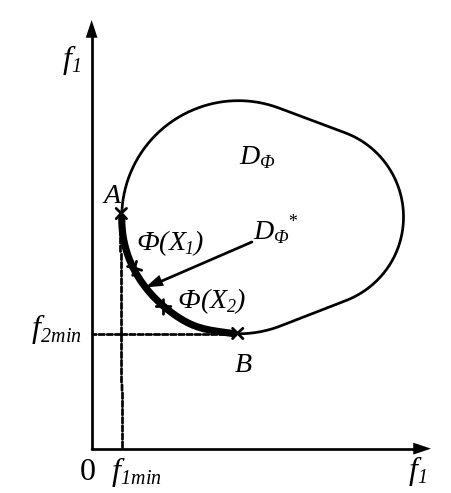
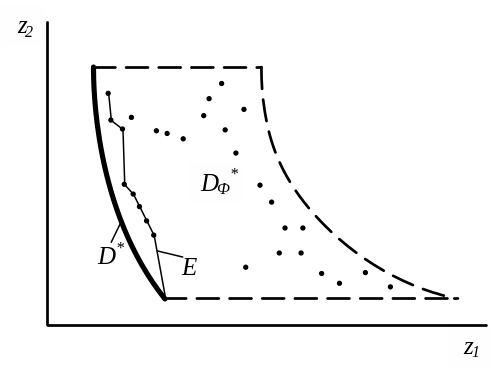
Рис. 8. Множество Парето

Для пояснения изложенного рассмотрим простейший метод, позволяющий приближенно находить множество Парето для случая двух критериев. На рис. 8, а построена область возможных значений в плоскости двух критериев. Исключение неэффективных точек в этом случае очень наглядно. Исключению подлежат все точки, образы которых в плоскости (f1, f2) расположены одновременно правее и выше образа исходной точки. В случае многих критериев геометрическая интерпретация аналогична.

После исключения неэффективных точек осталось всего 9 приближенно эффективных точек. Соединив их, получим приближенную компромиссную кривую E, которая вместе с точной компромиссной кривой D* построена на рис. 9, б. В качестве наилучшей среди исходной совокупности точек следует выбрать одну из этих 9 точек.

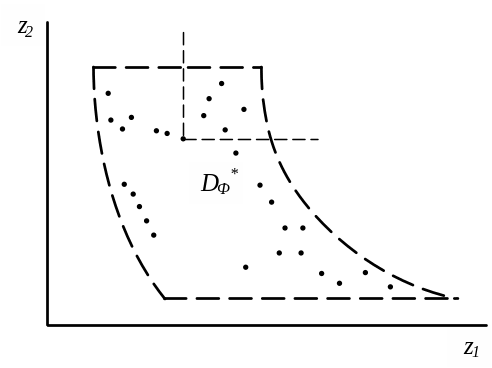а)

б)

Рис. 9. Построение области Парето

Например, Андрей лучше всех решает задачи, а по остальным критериям не выделяется. Зато Вера, Галя, Ира, Катя, Лариса имеют высокие значения остальных критериев, так что они в среднем превосходят Андрея, причем Вера лучше всех по успеваемости, а по остальным критериям не хуже других студенток. Тогда Андрей обзятельно попадает в множество Парето, т.к. он уникальный (единственный) по первому критерию, а от группы студенток в множество Парето попадает один представитель – Вера, хотя остальные студентки превосходят Андрея по нескольким критериям (число критериев здесь не имеет значения).

Таким образом, поиск оптимального решения (точки) может осуществляться в соответствии с рисунком 10.

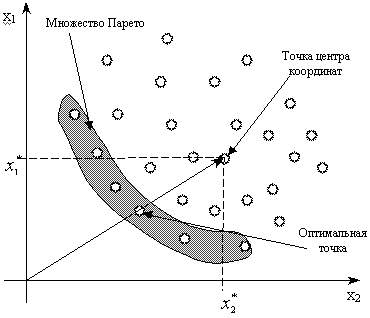
Рис. 10. Выбор оптимальной точки