1. Алгебраическая форма комплексного числа:

, , – мнимая единица,

– действительная часть комплексного числа, обозначается ,

– коэффициент при мнимой части комплексного числа, обозначается .

Каждому комплексному числу соответствует единственная точка плоскости (обратное справедливо).

2. Тригонометрическая форма комплексного числа:

, где

– модуль комплексного числа ,

– аргумент комплексного числа ,

, .

– главное значение аргумента комплексного числа ;

.

Распределение знака по четвертям:

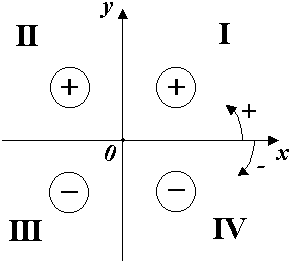
3. Показательная форма комплексного числа:

§ 3.2. Действия над комплексными числами

Комплексное число называется сопряженным к комплексному числу

Степени мнимой единицы:

…

…

…

… ,

В частных случаях:

ГЛАВА IV. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ.

Если каждому элементу множества некоторым способом поставлен в соответствие один элемент множества , то говорят, что задано отображение множества в множество . Записывают:

или

и изображают с помощью диаграмм Венна:

Пример:

ГЛАВА V. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

& – знак конъюнкции, логического умножения;

 – знак дизъюнкции, логического сложения;

1. , ;

2. , ;

3. , ;

4. , ;

5. ;

6. , , , ;

7. , ;

8. 

9. 

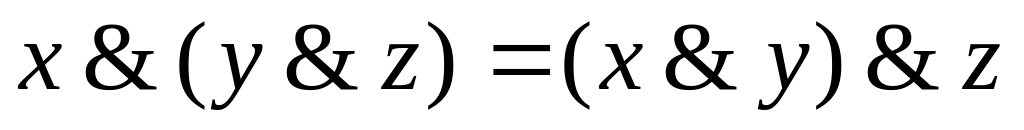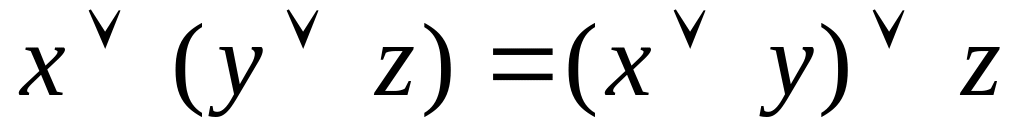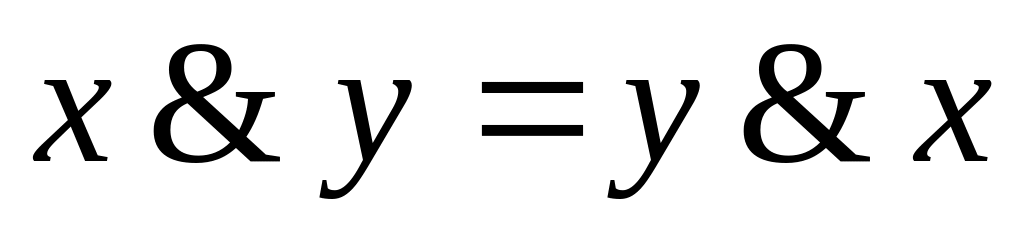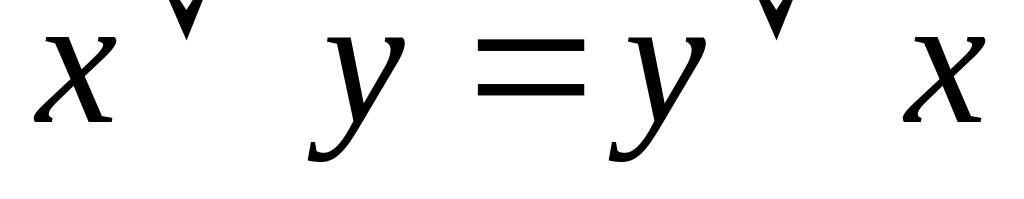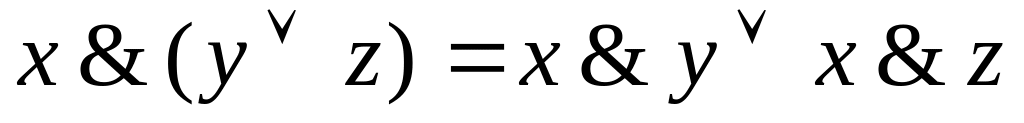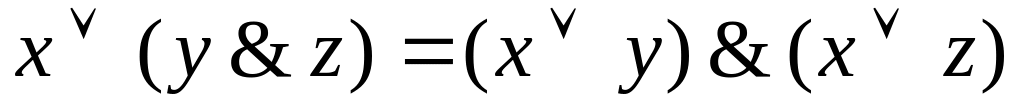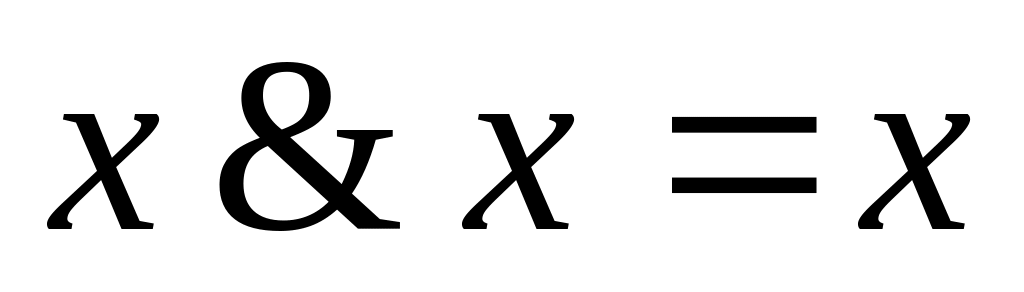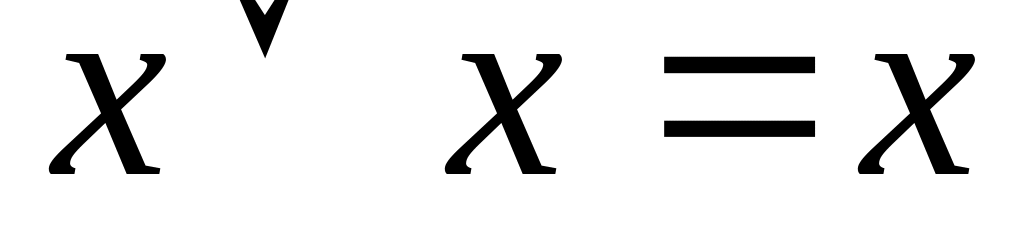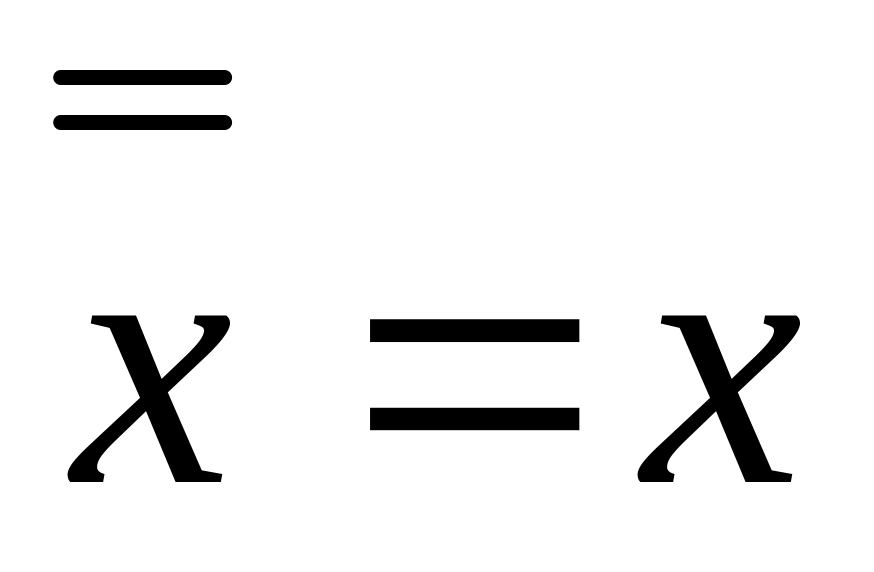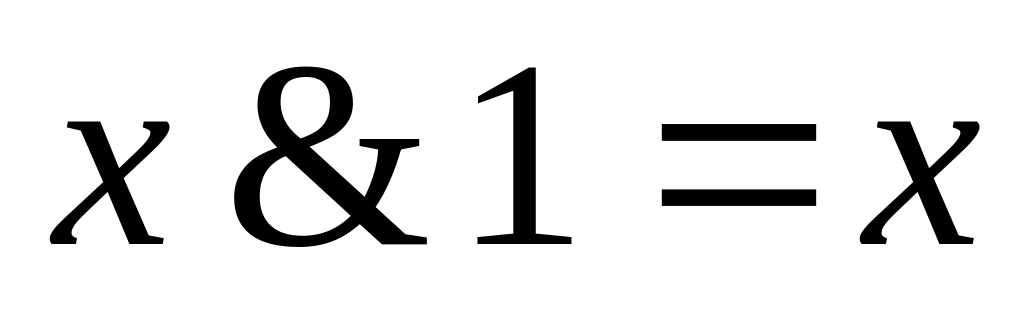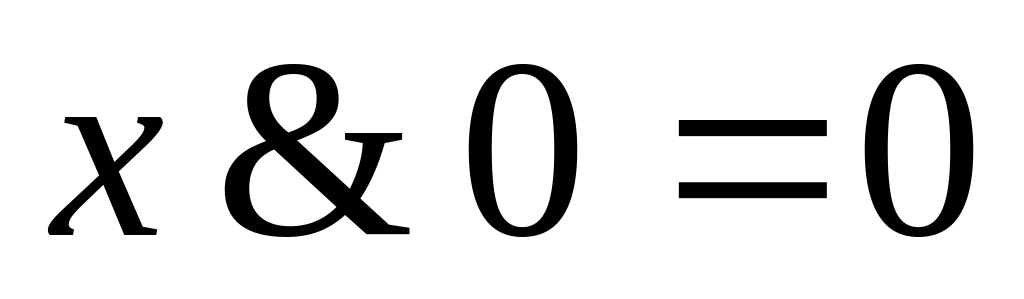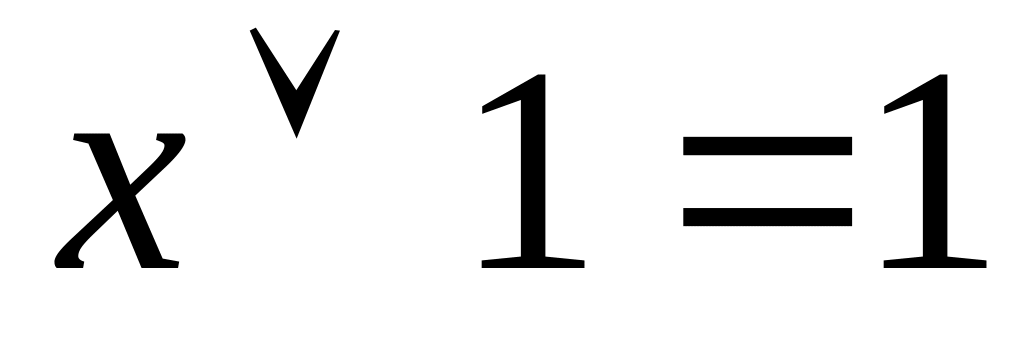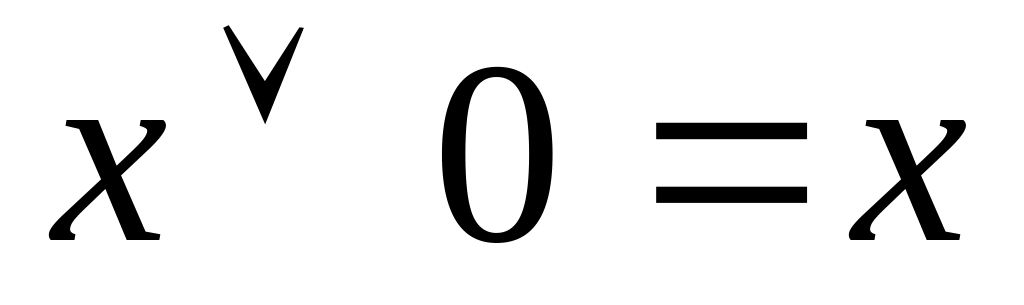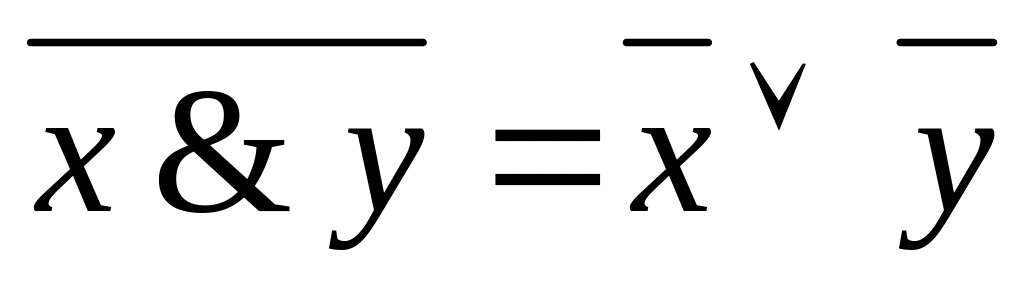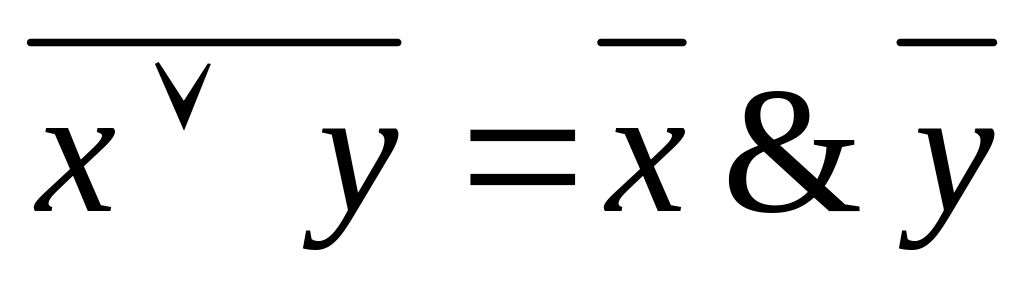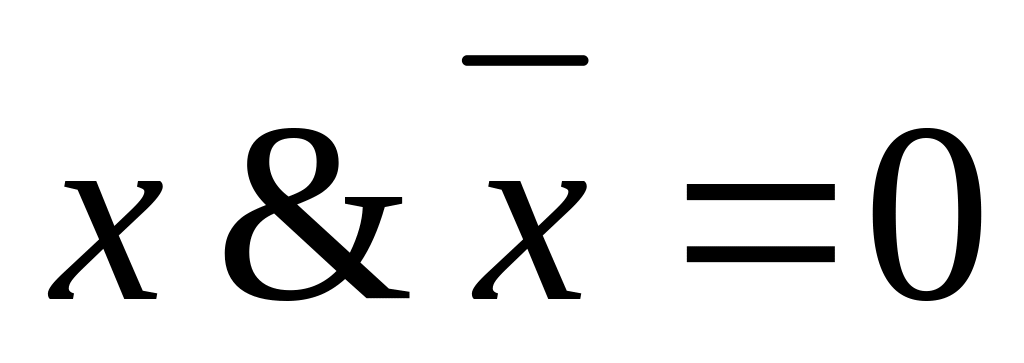
ГЛАВА VI. КОМБИНАТОРИКА.

Сочетания: (порядок элементов внутри выборки не важен)

Размещения: (порядок элементов внутри выборки важен)

Перестановки:

ГЛАВА VII. ЭЛЕМЕНТАРНАЯ АЛГЕБРА.

§ 7.1. Преобразования графиков функций.

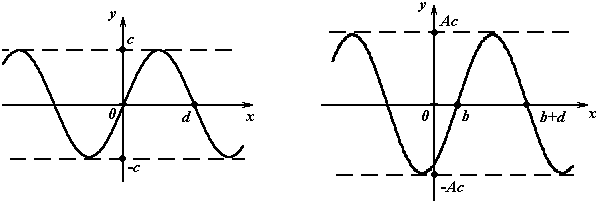
§ 7.2. Корень уравнения.

Если уравнение имеет единственный корень при , то уравнение так же имеет корень при .

ГЛАВА VIII. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

Правила вычисления пределов.

Если и , то

;

;

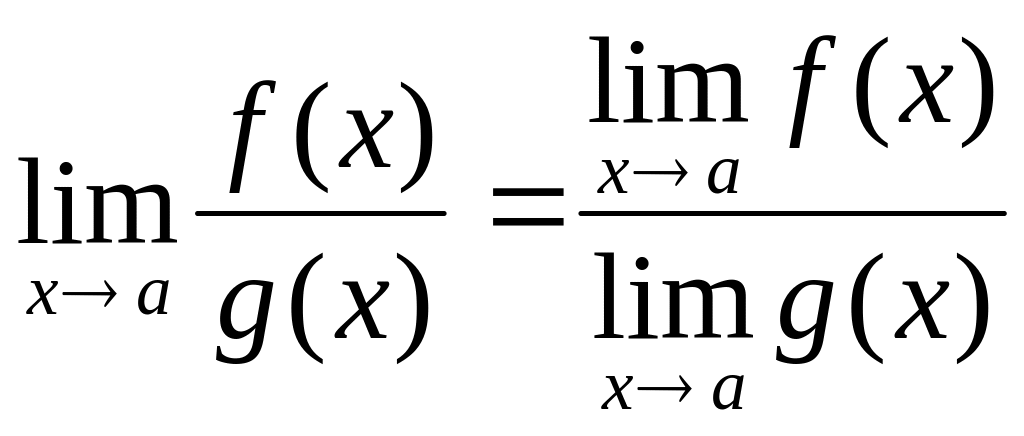, при ;

, .

Первый замечательный предел.

.

Следствия: ,

,

,

Второй замечательный предел.

.

Основные неопределенности.

, , , , .

Основные эквивалентные бесконечно малые величины.

, , , , при .

ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

Правила дифференцирования.

Если , – дифференцируемые функции,

то

1. 

2. 

3. 

Формулы дифференцирования:

,

,

,

Следствие: ,

Формула Лапиталя.

Дифференциал функции.

Применение дифференциального исчисления в исследовании функции

1. Если дифференцируемая функция возрастает (убывает) на отрезке , то .

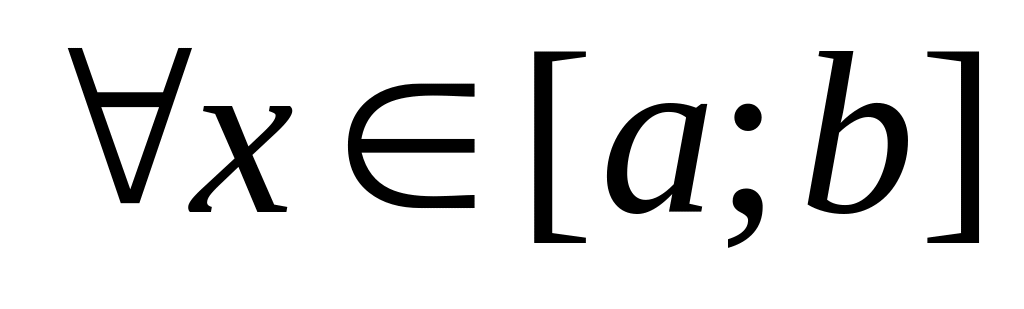
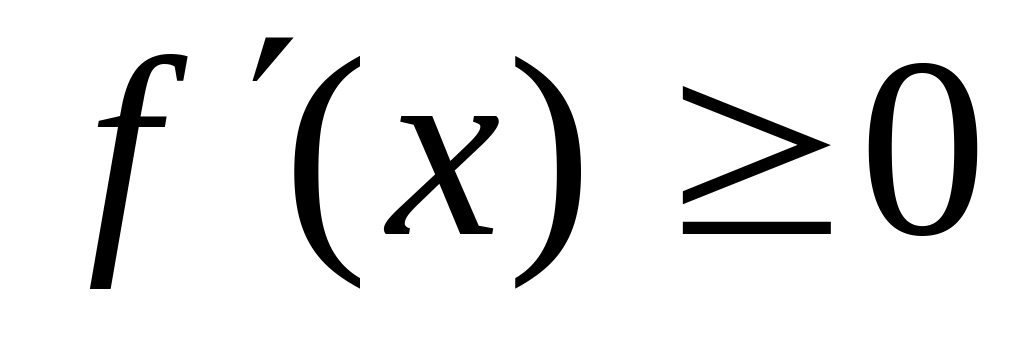
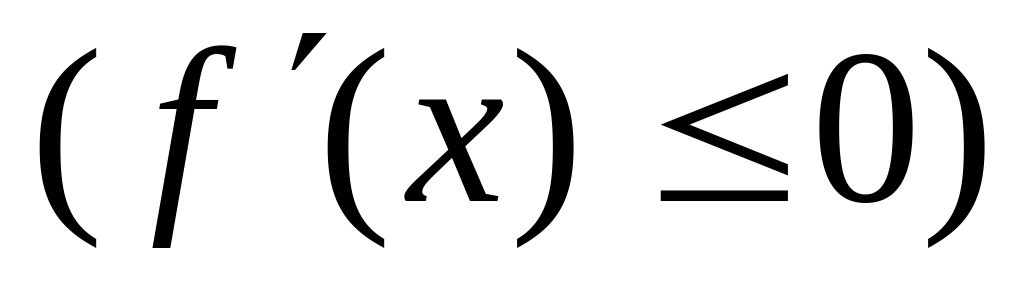2. Если дважды дифференцируемая функция выпукла (вогнута) на отрезке , то .

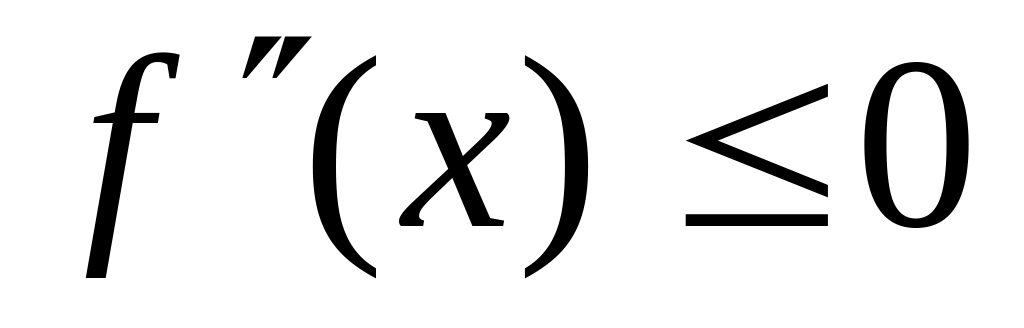
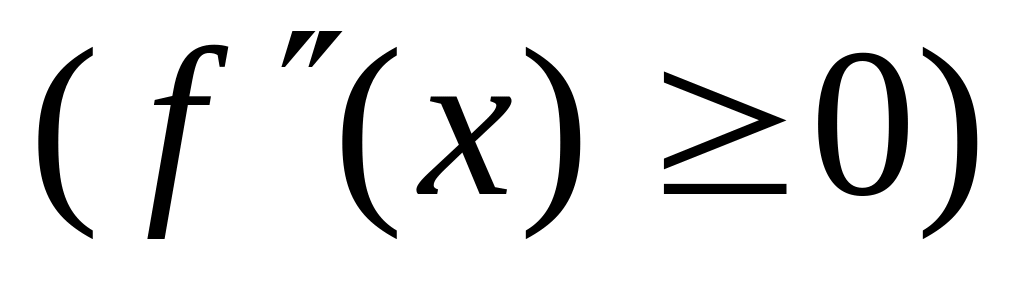Замечание: 1. Частные производные функции нескольких переменных находятся по тем же правилам и формулам, что и для функции одной переменной, полагая, что все переменные, кроме той, по которой производится дифференцирование, являются константами.

2. Градиент функции определяется по формуле:

ГЛАВА X. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.

§ 10.1. Неопределенный интеграл.

Таблица интегралов.

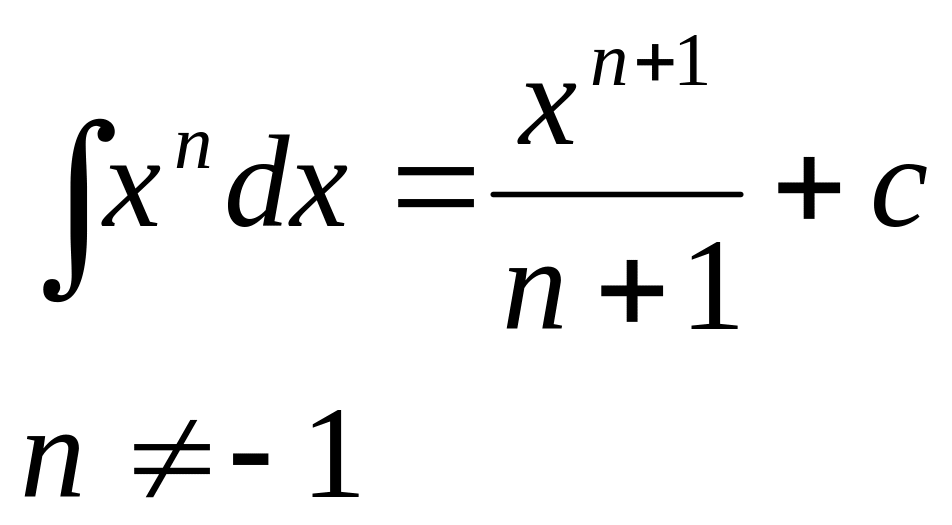
Некоторые тригонометрические формулы, применяемые при интегрировании:

, , ,

Разложение дроби на простейшие при интегрировании рациональных дробей:

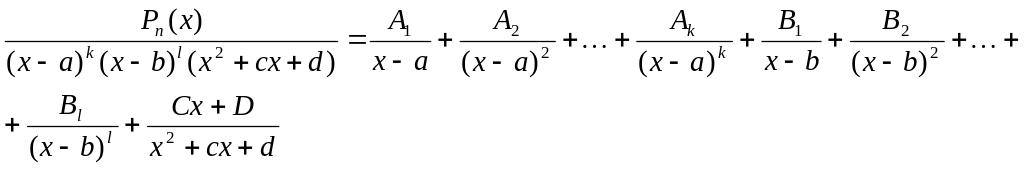
, т.е. дробь правильная

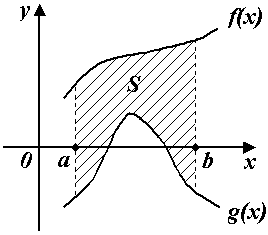
§ 10.2. Определенный интеграл.

§ 10.3. Двойной интеграл.

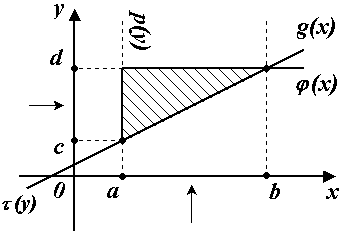
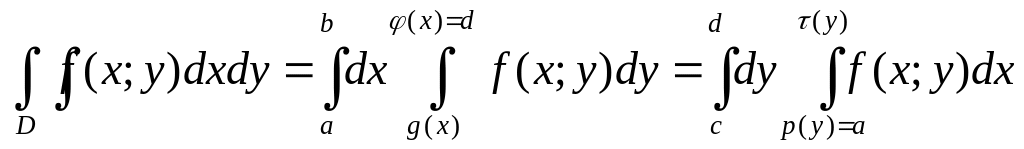
ГЛАВА XI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.

Уравнение, содержащее кроме неизвестной функции и её производные называется дифференциальным.

Например: – дифференциальное уравнение 1^го порядка.

– начальное условие.

Функция является частным решением дифференциального уравнения 1^го порядка, если выполняется:

Простейшими дифференциальными уравнениями первого порядка являются уравнения с разделяющимися переменными:

, где

и

Эти уравнения решаются путем деления на и последующего интегрирования уравнения.

– дифференциальное уравнение 2^го порядка,

; – начальные условия.

Частным случаем дифференциальных уравнений второго порядка являются линейные

неоднородные дифференциальные уравнения с постоянными коэффициентами:

Решение уравнений ищется в виде:

, где – общее решение однородного уравнения, соответствующего заданному,

– частное решение исходного уравнения.

строится в зависимости от корней характеристического уравнения:

Если , то

При ,

При ,