Формула Бернулли

Якоб Бернулли установил, что вероятность ровно m успехов в серии из n повторных независимых испытаний вычисляется по следующей формуле:

Значение m₀, при котором число P_n(m) является максимальным из множества {P_n(m)}, называется наивероятнейшим, и оно удовлетворяет условию:

np - q m₀ np+ p

Вероятности называются биномиальными в силу того, что правая часть формулы представляет собой общий член разложения бинома Ньютона: 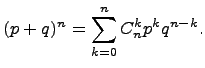Так как , то из формулы бинома Ньютона следует, что сумма всех биномиальных вероятностей равна 1:

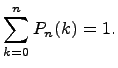
Другие достижения.

Но теория вероятностей была не единственной наукой, к которой обращался Бернулли. Он также многое сделал для развития дифференциального исчисления, обогатил анализ бесконечно малых и теорию рядов, занимался аналитической геометрией.

Дифференциальное уравнение Бернулли

Будучи профессором математики Базельского университета, Бернулли ознакомился с первым мемуаром Готфрида Лейбница по дифференциальному исчислению (1684) и, обнаружив трудные места, написал письмо Лейбницу с просьбой разъяснить несколько тёмных мест. Ответ он получил только спустя три года (Лейбниц тогда был в длительной командировке в Париже); за это время Якоб Бернулли самостоятельно освоил «Новый метод», и надобность в консультации отпала. Якоб совместно Иоганном овладели дифференциальным и интегральным исчислениями настолько, что вскоре смогли приступить систематическому развитию метода. Образовавшийся триумвират — Лейбниц и братья Бернулли — менее чем за двадцать лет чрезвычайно обогатил анализ бесконечно малых.

Новшество заключается в предложенном методе решения дифференциальных уравнений 1-го порядка вида: y’ + P(x)y = Q(x)y^a, где Р, Q — заданные непрерывные функции от х, а — постоянное число, отличное от 0 и 1. Введением новой функции z=y^1-a уравнение Бернулли сводится к линейному дифференциальному уравнению относительно z.

Уравнение названо в честь Якоба Бернулли, опубликовавшего его в 1695 году, а метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.

Принцип Бернулли

Можно предположить, что Якоб независимо от Блеза Паскаля изобрел метод полной математической индукции; долгое время его называли «принцип Бернулли». Якоб в своём основном труде приводит ссылки на своих предшественников и в теории вероятностей, и в комбинаторике. Паскаль среди них не упоминается.

Лемниската Бернулли

В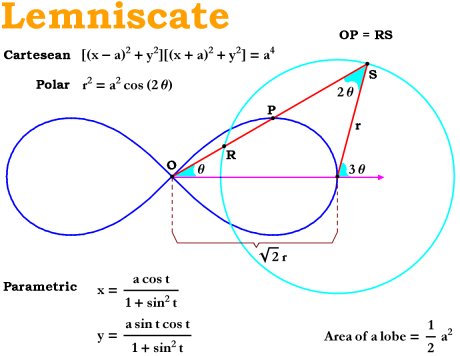 статье 1690 года Якоб Бернулли ввел полярные координаты. Благодаря этому, он впервые построил и изучил несколько новых кривых, в том числе лемнискату Бернулли, спирали. Он открыл много интересных свойств этих кривых, некоторые из свойств (инвариантность относительно преобразований) его так поразили, что он завещал изобразить на его могильном камне логарифмическую спираль с надписью «Измененная, возрождаюсь прежней».

Лемниската названа в честь Якоба, так как он положил начало её изучению. Лемниската – это плоская алгебраическая кривая, определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами. Бернулли назвал эту кривую lemniscus, название происходит от греч. λημνισχος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Впервые уравнение лемнискаты было опубликовано в статье Curvatura Laminae Elasticae Якоба Бернулли в журнале Acta eruditorum в 1694 году.

Многочлен Бернулли

Это многочлены, названные в честь Бернулли, возникающие при изучении многих специальных функций, в частности ζ-функции Римана и ζ-функции Гурвица, также являются частным случаем последовательности Аппеля. В отличие от ортогональных многочленов, многочлены Бернулли замечательны тем, что число корней в интервале [0,1] не увеличивается с увеличением степени многочлена. При неограниченном увеличении степени, многочлены Бернулли приближаются к тригонометрическим функциям.

Многочлен имеет вид: , где  — биномиальные коэффициенты,  — числа Бернулли.

Числа Бернулли

Это последовательность рациональных чисел В₀, В₁, В₂, …, впервые рассмотренная Якобом Бернулли в связи с вычислением суммы натуральных чисел одинаковых степеней, он описал их в своём главном труде. В математическом анализе Числа Бернулли появляются как коэффициенты разложения некоторых элементарных функций в степенные ряды. Для вычисления чисел известны рекуррентные формулы, позволяющие последовательно вычислять эти числа ( ), а также явные формулы (имеющие довольно сложный вид).

Большой интерес представляют свойства этих чисел. Например:

• Все числа Бернулли с нечётными номерами, кроме 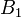, равны нулю, а знаки чисел Бернулли с чётными номерами чередуются.

• Числа Бернулли являются значениями многочленов Бернулл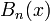и при :

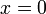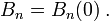
• Числа Бернулли часто входят в коэффициенты разложения элементарных функций в степенной ряд. Для тангенса: .
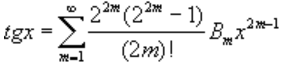