Практическое занятие №19

Тема: Решение задач на приложения двойных интегралов

Цель: Формирование навыков решения задач на приложения двойных интегралов

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Площадь плоской областив прямоугольных координатах вычисляется по формуле

; (1)

а в полярных координатах – по формуле

. (2)

Объем цилиндрического тела, ограниченного сверху поверхностью , снизу областьюи сбоку прямой цилиндрической поверхностью, вырезающей на плоскостиобласть(рис. 1), вычисляется по формуле

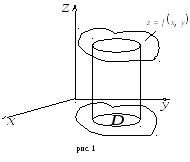
(3)

Примеры

Задание:Вычислить объем тела, ограниченного поверхностями,,,.

Решение:Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в первом октанте. Сверху тело ограничено плоскостью, сбоку параболическим цилиндроми плоскостямии. Найдем точки пересечения параболыи прямой:. Таким образом, получим одну точку пересечения.

Значение не рассматриваем, так как цилиндр расположен в первом октанте. Областьзапишем в виде системы неравенстви.

Согласно формуле (3), получим

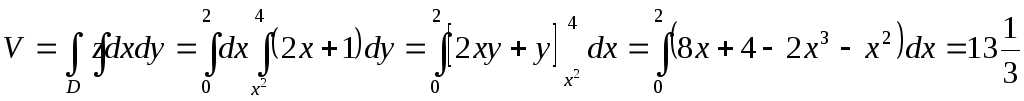(куб. ед.)

Задания для самостоятельной работы

1. Вычислить площадь плоской фигуры в прямоугольных координатах, если область ограничена линиями:

1) ,; 2),,;

3) ,; 4),;

5) ,; 6),.

2. Вычислите объемы тел, ограниченных заданными поверхностями:

1) ,,,,;

2) ,,,,;

3) ,,,,;

4) ,,,,;

5) ,,,.

Вопросы для самоконтроля:

1. По какой формуле вычисляется площадь плоской области в прямоугольных координатах?

2. По какой формуле вычисляется площадь плоской области в полярных координатах?

3. По какой формуле находится объем тела, ограниченного поверхностями?

Практическое занятие №20

Тема: Решение дифференциальных уравнений первого порядка с разделяющимися переменными; однородных дифференциальных уравнений первого порядка и линейных дифференциальных уравнений первого порядка

Цель: Формирование навыков решения дифференциальных уравнений первого порядка с разделяющимися переменными; однородных дифференциальных уравнений первого порядка и линейных дифференциальных уравнений первого порядка

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Дифференциальным уравнениемназывается уравнение, связывающее между собой независимую переменную, искомую функциюи ее производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

, ,.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Порядкомдифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

Решением(илиинтегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Общим решением(илиобщим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Частным решениемдифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.

Дифференциальным уравнением первого порядканазывается уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

.

Для решения этого уравнения нужно сначала разделить переменные:

,

а затем проинтегрировать обе части полученного равенства:

.

Уравнение вида , гдеи- функции от, называетсялинейным дифференциальным уравнением первого порядка. В частностиимогут быть постоянными величинами.

Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки , гдеи- новые функции от.