Примеры

Задание 1:Решить уравнение:.

Решение:Составим характеристическое уравнение и найдем его корни:. Отсюда следует, что,. Так как корни характеристического уравнения действительные и разные, то общее решение данного дифференциального уравнения согласно формуле (3) запишется так:.

Задание 2:Найти частное решение уравнения, еслиипри.

Решение:Составим характеристическое уравнение. Решая его, получим,,. Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид:, то есть.

Для нахождения искомого частного решения нужно определить значения постоянных и. Подставив в общее решение значенияи, получим.

Продифференцировав общее решение и подставив в полученное выражение значения и, имеем, отсюда следует, что. Из данного выражения находим:,.

Таким образом, искомое частное решение имеет вид .

Задание 3:Решить уравнение.

Решение:Составим характеристическое уравнение и найдем его корни:,. Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (4) общее решение данного дифференциального уравнения записывается в виде.

Задание 4:Найдите частное решение уравнения, еслиипри.

Решение:Так как характеристическое уравнениеимеет равные действительные корни, то общее решение данного дифференциального уравнения записывается в виде

.

Дифференцируя общее решение, имеем

.

Подставив начальные данные в выражение для и, получим систему уравнений

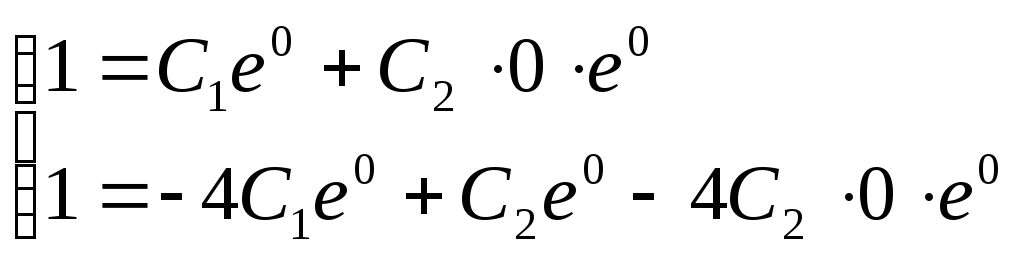, или , откудаи. Следовательно, искомое частное решение имеет вид.

Задания для самостоятельной работы

1. Решите уравнения:

1) ; 2);

3) ; 4);

5) ; 6);

7) ; 8).

2. Найдите частные решения уравнений:

1) ;ипри;

2) ;ипри;

3) ;ипри.

3. Решите уравнения:

1) ; 2);

3) .

4. Найдите частные решения уравнений:

1) ;ипри;

2) ;ипри.

Вопросы для самоконтроля:

1. Какие дифференциальные уравнения называются уравнениями второго порядка?

2. Какие уравнения называются линейными однородными дифференциальными уравнениями второго порядка?

3. Какой вид имеет характеристическое уравнение? Для чего необходимо его нахождение?

4. Какие случаи возможны при нахождении общего решения дифференциального уравнения второго порядка?

Практическое занятие №22

Тема: Нахождение суммы ряда по определению. Исследование сходимости положительных рядов

Цель: Формирование навыков нахождения суммы ряда по определению и исследования сходимости положительных рядов

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Числовым рядомназывается сумма вида

, (1)

где числа ,,, …,, …, называемыечленами ряда, образуют бесконечную последовательность; членназываетсяобщим членомряда.

Суммы

,

,

,

………………

,

составленные из первых членов рядя (1), называются частичными суммамиэтого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм ,,, …,…. Если при бесконечном возрастании номерачастичная сумма рядастремится к пределу, то ряд называется сходящимся, а число- суммой сходящегося ряда, то естьили. Эта запись равносильна записи.

Если частичная сумма ряда (1) при неограниченном возрастаниине имеет конечного предела (в частности, стремится кили к), то такой ряд называетсярасходящимся.

Если ряд сходится, то значение при достаточно большомявляется приближенным выражением суммы ряда.

Разность называетсяостатком ряда. Если ряд сходится, то его остаток стремится к нулю, то есть, и наоборот, если остаток стремится к нулю, то ряд сходится.

Для знакоположительных числовых рядов имеет место признак сравнении, при помощи которого можно установить сходимость или расходимость.

Признак сравнения. Если члены положительного ряда

, (2)

начиная с некоторого номера, не превосходят соответствующих членов ряда

, (3)

то из сходимости ряда (3) следует сходимости ряда (2), а из расходимости ряда (2) следует расходимость ряда (3).

При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия, которая сходится прии расходится при, игармонический ряд, являющийся расходящимся рядом.