1.4. Включение r, l на постоянное напряжение

Пусть после коммутации реализуется цепь следующего вида (рис 1.4):

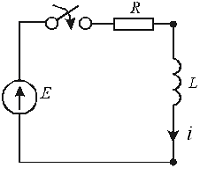
Рис.1.4.1 Схема цепи

Ток в индуктивности до коммутации

Составим дифференциальное уравнение цепи после коммутации:

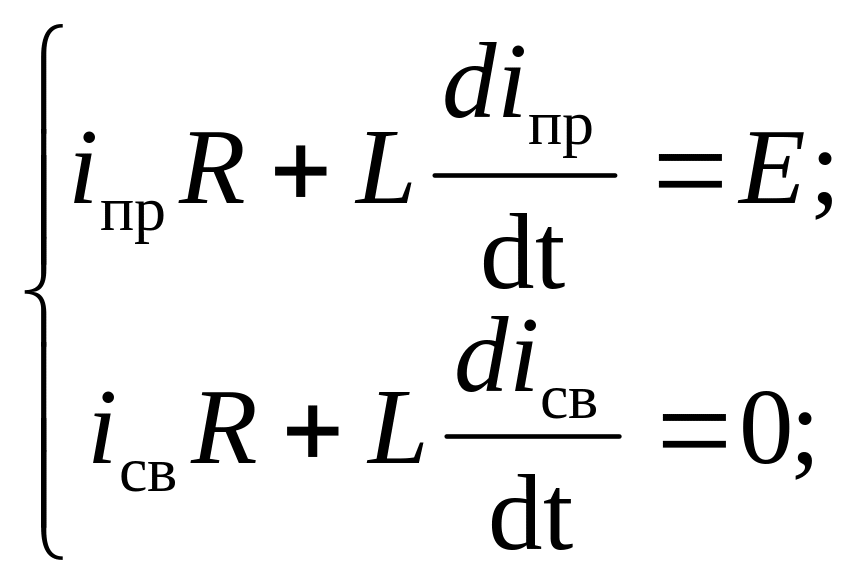
Поскольку элементный состав цепи не изменился, т.е. параметры цепи L и R те же, то и характеристическое уравнение также не изменилось:

Для получения окончательного решения необходимо получить постоянную интегрирования А, воспользовавшись для этого независимым начальным условием при t = 0:

Окончательно.

Проверка:

Используя полученную функцию для тока, найдем зависимости u_R(t) и u_L(t):

Проверка:

Используя второй закон Кирхгофа, проверим правильность расчетов.

Анализ полученных выражений показывает, что индуктивность в момент коммутации может рассматриваться как разрыв цепи. По найденным функциям построим соответствующие графики (рис 1.4.2.):

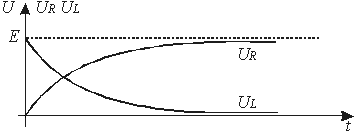
Рис. 1.4.2. Зависимости токов и напряжений в переходном процессе при включении катушки индуктивности к источнику постоянного напряжения

1.5. Включение цепи r-l к источнику синусоидального напряжения

Подключим цепь R-L к источнику синусоидального напряжения:

Решение для тока аналогично цепи с источником постоянного напряжения

где

Мгновенное значение принужденного тока:

полный ток:

При t = 0 найдем значение А:

окончательно

Проверка:

i(0) = 0; i(∞) – синусоидально изменяющаяся функция.

По найденному току легко рассчитываются u_R(t), u_L(t).

Построим график тока i(t) и рассмотрим особенности переходного процесса, определяемые параметрами цепи R, L и фазой напряжения источника.

Пусть φ_i = φ_u - φ > 0. График i(t) представлен на рис. 1.5.

Рис.1.5. Зависимость i(t) при питании цепи от источника

синусоидального напряжения

Из построенной зависимости видно, что спустя время t равное примерно половине периода синусоидального тока после коммутации, значение тока превышает амплитудное значение его установившейся составляющей.

1.6. Общая методика расчета переходных процессов

классическим методом на примере цепи второго порядка

1. Рассчитывается режим работы цепи до коммутации и определяются независимые начальные условия u_c(-0), i_L(-0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа, описывающая процесс после коммутации. Находится решение относительно необходимой величины тока или напряжения. По виду однородного дифференциального уравнения составляется характеристическое уравнение. Характеристическое уравнение также может быть составлено по выражению для входного сопротивления цепи по переменному току Z(j ), в котором j заменили на р. Полученное выражение Z(p) = 0 и представляет собой характеристическое уравнение.

3. Представляем решение искомой величины в виде суммы принужденной и свободной составляющих.

4. Рассчитываем установившийся режим работы цепи после коммутации.

5. Для определения двух неизвестных постоянных интегрирования А_i продифференцируем решения для определяемого тока или напряжения и перепишем полученную систему уравнений для момента времени t = 0:

i(0) = i_пр(0) + A₁+А₂;

t=0 = t=0 +A₁р₁+А₂р₂.

6. Для определения зависимых начальных условий i(0) и t=0 составим для послекоммутационной схемы систему уравнений по законам Кирхгофа для момента времени t=0, перепишем ее относительно свободных составляющих токов и напряжений, подставим в нее известные независимые начальные условия и рассчитаем необходимые зависимые начальные условия.

7. Запишем окончательный результат в виде суммы определенной в третьем пункте принужденной составляющей искомого тока или падения напряжения и свободной составляющей этой величины , рассчитанной в п.6.

В качестве примера проведем расчет для электрической схемы, представленной на рис.1.6.

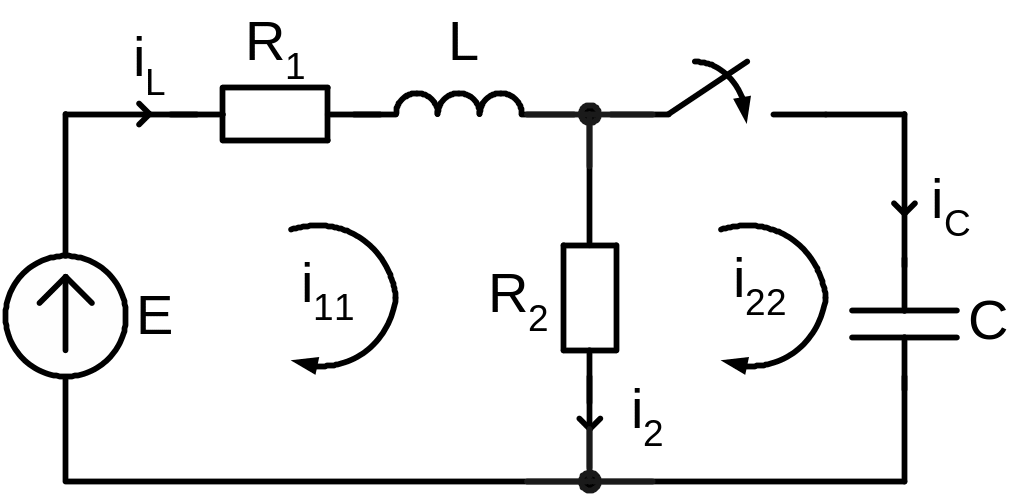
Рис.1.6. Цепь с двумя реактивными элементами

Заданы параметры: R₁=R₂=10 Ом, L=5 мГн, С=10 мкФ, Е=100 В. Определить i₂(t).

1. Независимые начальные условия:

;

u_C(-0)=u_C(0)=0.

2. Для получения характеристического уравнения составим систему уравнений, например, по методу контурных токов:

Разобьем данную систему на две: относительно принужденной и свободной составляющих:

Используя систему уравнений для свободных токов, составим характеристическое уравнение . Для этого подставляем свободные токи в виде i_св=Аe^pt, их производные как pi_св , а интегралы - i_св/p. Составим главный определитель полученной системы уравнений, который и представляет собой характеристическое уравнение данной цепи, и найдем его корни:

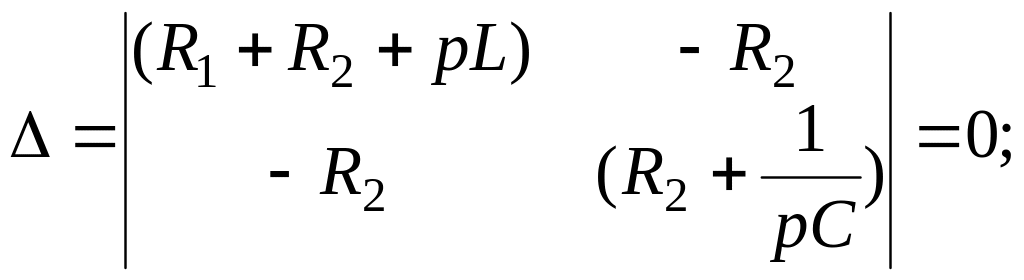
Так как R₁=R₂=R, то

После подстановки исходных данных уравнение примет вид

p² + 12∙10³p + 4∙10⁷ = 0;

p₁₂ = - 6∙10³ j∙2∙10³ = -α jω₁.

Так как корни комплексно сопряженные, переходный процесс имеет периодический или колебательный характер.

3. Представляем решение в виде суммы принужденной и свободной составляющих тока:

i₂= i_2пр+ i_2св = i_2пр+ A sin( + ).

4. Рассчитываем установившийся режим работы цепи после коммутации:

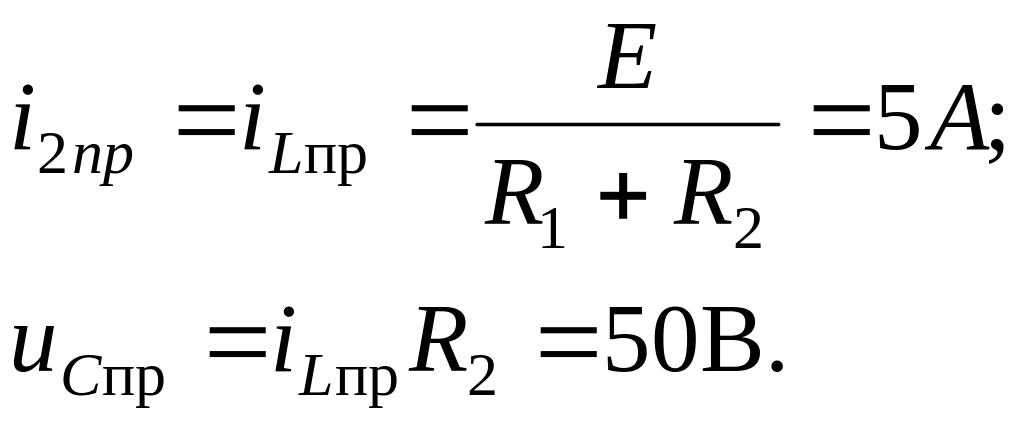
5. Для определения двух неизвестных постоянных интегрирования А и продифференцируем решение для тока i₂(t) и перепишем полученную систему уравнений для момента времени t = 0:

i₂(0) = 5 + A sinψ;

t=0 = A(- sin + ₁cos ).

6. Для определения двух зависимых начальных условий i₂ и воспользуемся законами Кирхгофа и законами коммутации:

u_C(0)-i₂(0)R₂=0; i₂(0)=0;

5 + A sin =0;

Таким образом, окончательный вид система уравнений относительно постоянных интегрирования имеет вид

Её решение:

7. Окончательное решение для тока i₂(t) имеет вид

i₂(t) = 5 + 11.2·e^-6000t·sin (2000t - 26.6˚).

Проверка:

при t = 0 i₂(0) = 5 + 11.2sin(-26.6˚) = 0;

при t = i( ) = 5 A.