5. Степень множества

Если A  множество, то 2^A обозначает множество всех подмножеств множества A и называется степенью этого множества.

Упражнение.

1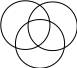 . Используя операции над множествами, выразить через множества A, B и C множества 1  7 на следующей диаграмме Венна.

A 1 2 3 B

4 5 6

C 7

2. Проверьте справедливость тождеств (AB)  (CD) = (AC) (BD) и (AB)(CD) = (AC)  (BD).

1.1.4. Мощность множеств

Характеристика множеств, представляющая количество содержащихся в них элементов, называется мощностью множеств.

Если некоторое множество A содержит конечное число элементов, то его мощность |A| равна числу элементов этого множества. Для бесконечных множеств понятие количества элементов требует уточнения.

В общем случае понятие мощности произвольных множеств определяется через их равномощность.

Определение

Множества A и B называются равномощными, если их элементы можно поставить во взаимно однозначное соответствие.

То есть можно определить такое множество пар (a, b), первая компонента которых принадлежит A, а вторая компонента принадлежит B. При этом для каждого a A существует одна пара, первая компонента которой равна a. Аналогично, для каждого элемента b B существует одна пара, вторая компонента которой равна b.

Определение

Мощностью множества A называется семейство всех множеств, равномощных A.

Поскольку всякое множество равномощно самому себе, то мощность всякого множества является непустым семейством. Поэтому мощность является реальной характеристикой всякого множества. Мощность произвольного множества A обозначается символически как |A|.

Множество A  конечно, если оно пустое или равномощно некоторому началу {1, 2, ... , k} множества натуральных чисел N. Для непустого конечного множества A, состоящего из k элементов, принято использовать число k в качестве обозначения мощности этого множества.

Мощность пустого множества считается равной нулю.

Множество A называется счетно-бесконечным, если оно равномощно множеству натуральных чисел N. Мощность счетно-бесконечного множества обозначается как ₀.

Множество A называется счетным, если оно конечное или счетно-бесконечное. Содержательно счетность множества означает, что его элементы можно последовательно пересчитать подобно тому, как могут быть пересчитаны все элементы множества натуральных чисел. Для этого достаточно организовать пересчет N, при котором для каждого натурального числа указывается соответствующий ему элемент счетного множества A.

Замечание. Счетные множества объектов  это основной вид множеств объектов, изучаемых в дискретной математике.

Упражнение. Показать, что если a равномощно b, а b равномощно c, то a равномощно c.

Рассмотрим некоторые свойства счетных множеств.

Теорема 1.1

Объединение любых двух счетных множеств является счетным множеством.

Доказательство

Пусть A и B  счетные множества. Возможны следующие случаи.

1. Если A и B  конечные множества, то A B состоит из конечного числа разных элементов, т.е. является счетным.

2. Если A  конечное, а B  счетно-бесконечное, и A={a₁, ... , a_k}, B = {b₁, ... , b_i, ...}, где элементы A и B перечислены в порядке соответствия элементов A и B элементам множества {1, ... , k} и множеству натуральных чисел соответственно.

Удалим из A элементы, содержащиеся в B. В результате получим новое множество {a_j1, ... , a_jl}, которое может оказаться пустым.

Тогда множество {a_j1, . . . , a_jl, b₁, . . . , b_i, ...}, в котором элементы перечислены в порядке соответствия возрастающим элементам множества натуральных чисел, является множеством, равномощным N.

3. Множества A и B  счетно-бесконечные. Тогда их можно представить в виде:

A = {a₁, . . . , a_i, . . .}, B = {b₁, . . . , b_i, . . .}.

Рассмотрим процесс последовательного выписывания в один список первых, вторых, третьих и последующих элементов этих множеств: a₁ и b₁, a₂ и b₂, a₃ и b₃ и т.д.

При этом в список не включаются такие из выбираемых элементов, которые уже встречались ранее.

Этот процесс позволяет записать все элементы множества A  B в виде счетной бесконечной последовательности c₁, . . . , c_j, . . . .

Такая последовательность содержит все элементы AB по одному разу, в сопоставлении их с натуральными числами, так что элемент c_i соответствует числу i.

Следовательно, A B  является счетным множеством.

Доказательство окончено.

Упражнение. Доказать, что пересечение любых двух счетных множеств является счетным.

Нетрудно убедиться в том, что объединение и пересечение всякого конечного числа счетных множеств также является счетным множеством. В некоторых случаях приходится иметь дело с объединением или пересечением счетно-бесконечного семейства счетных множеств, т.е. рассматриваются множества, представляемые в виде: A = .

Здесь запись обозначает бесконечное объединение множеств A₁ ... A_{i ...} При этом A_i = {a_i1, ... , a_ij, ...}.

Здесь a_ij  j-й по порядку пересчета элемент множества A_i.

Как следует из приводимой далее теоремы, такие множества также оказываются счетными.

ТЕОРЕМА 1.2

Счетно-бесконечное объединение счетных множеств является счетным множеством.

Доказательство

Проведем доказательство для простейшего случая, когда все множества A_i  счетно-бесконечные и непересекающиеся. Остальные случаи могут быть предложены в качестве упражнения.

Выпишем элементы множества в виде таблицы:

a _{1 1} a_{1 2} a _{1 3} . . . a _{1 j} . . .

a _{2 1} a _{2 2} a _{2 3} . . . a _{2 j} . . .

a _{3 1} a _{3 2} a _{3 3} . . . a _{3 j} . . .

. . . . . .

. . . . . . . . . .

a _{i 1} a _{i 2} a _{i 3} . . . a _{i j} . . .

. . . . . . . . . .

Последовательно пройдем по всем элементам таблицы в порядке, указанном стрелками, выписав все элементы множества . Элементы таблицы последовательно проходят по диагоналям таблицы, начиная с левого верхнего угла, а на диагоналях - в направлении сверху вниз.

Такой пересчет элементов ставит их в однозначное соответствие элементам множества натуральных чисел.

Доказательство окончено.

Определим натуральное число n, равное порядковому номеру элемента a_ij в выписанном множестве .

Отметим следующие свойства пересчета элементов:

1) число элементов i-й по порядку диагонали равно i;

2) при движении по диагонали сверху вниз первый индекс элементов возрастает, а второй убывает;

3) сумма индексов элементов i-й диагонали постоянна и равна i + 1.

Воспользуемся данными свойствами. Тогда справедливы следующие выводы:

а) элемент a_ij находится на (i+j-1)–й, начиная от левого верхнего угла диагонали, поэтому число элементов диагоналей, предшествующих диагонали, содержащей a_ij, равно:

1 + 2 + ... + i + j 2 = (i + j  1) (i + j  2) / 2;

2. элемент a_ij является j-м по порядку элементом на диагонали с номером i + j  1.

Поэтому порядковый номер a_ij в выписанном множестве равен: ((i + j  1) (i + j  2) / 2) + j .