1 Цифровые интегральные микросхемы

1.1 Основы алгебры логики

1.1.1 Основные определения

В зависимости от отсутствия или наличия элементов па­мяти цифро- вые устройства делятся на комбинационные устройства (КУ) и конечные автоматы (последовательные устройства). Выходные сигналы КУ определя- ются совокупностью (комбина­цией) входных сигналов, действующих на некотором интервале времени. Наличие элементов памяти в конечных автоматах обус­ловливает зависимость выходных сигналов на рассматрива- емом интервале от совокупности входных сигналов, действующих как на этом интервале времени, так и на ряде предшествующих интер­валов. В комбинационном устройстве связь между входны­ми x₁, x₂,… х_n и выходными у₁, у₂, …, у_n сигналами цифрового устройства может быть задана функциями вида:

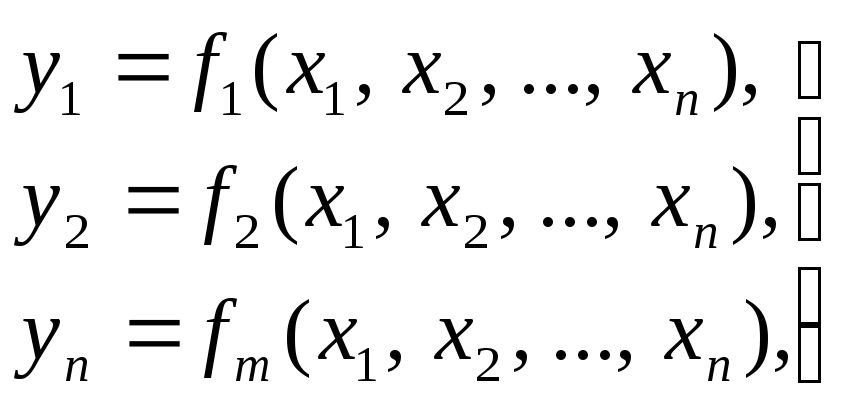(1.1)

Особенность входных сигналов (независимых переменных) и выходных сигналов (функций) заключается в том, что они могут принимать только два значения: 1 или 0. Такие функции называ­ются логическими, или переключательными, или булевыми.

Раздел математики, который изучает логические функции, на­зывается алгеброй логики.

Наиболее часто логическая функция задается с помощью таб­лицы. В строках таблицы записываются все возможные наборы значений аргументов и указываются значения логической функ­ции, которые они принимают на каждом наборе. Эту таблицу принято называть таблицей истинности. Для m переменных мо­жет быть 2^m различных наборов. Пример логической функции трех аргументов x₁, х₂, x₃ приведен в таблице 1.1.

Таблица 1.1

Номер набора	Х3	Х2	Х1	У	Номер набора	Х3	Х2	Х1	У
0	0	0	0	0	4	1	0	0	0
1	0	0	1	0	5	1	0	1	1
2	0	1	0	0	6	1	1	0	1
3	0	1	1	1	7	1	1	1	1

Если рассматривать наборы x₃, x₂, x₁ как двоичные числа, то удобно ввести десятичную нумерацию наборов. Например, набор x₃= 1, х₂=1, x₁ = 0 имеет номер 6.

Вместо таблицы истинности иногда логическую функцию удоб­но задавать словесным описанием. Например, функция у, заданная таблице 1.1, может быть словесно определена так: у=1 в том случае, если не менее двух аргументов принимают значение 1.

По способу соединений элементов цифровые устройства делят­ся на два типа: на устройства со статическими (потенциальны­ми) связями между элементами и устройствами с динамическими (импульсными и импульсно-потенциальными) связями между эле­ментами. Учитывая широкое распространение в интегральной схе­мотехнике элементов с потенциальными связями, в дальнейшем будем ориентироваться только на элементы этого класса.

1.1.2 Некоторые логические функции и реализующие их логические элементы

Логическое сложение (дизъюнкция). Логическая функция у является логической суммой (дизъюнкцией) переменных y=f(х₁, х₂, ..., х_n), если она равна 1 в тех наборах, на которых хотя бы одна независимая переменная равна 1, и равна 0 в остальных набо­рах. Пример функции у, являющейся логической суммой двух переменных х₁ и х₂, приведен в таблице 1.2.

Таблица 1.2 Таблица 1.3

Номер набора	Х2	Х1	У		Номер набора	Х2	Х1	У
0	0	0	0		0	0	0	0
1	0	1	1		1	0	1	0
2	1	0	1		2	1	0	0
3	1	1	1		3	1	1	1

Логическое сложение двух переменных принято обозначать следующим образом: y=х₁  х₂, а логическое сложение n переменных

y=x₁ х₂ … х_n (2)

Схема, с помощью которой из входных переменных х₁, х₂, ..., х_n образуется их логическая сумма, называется логическим эле­ментом ИЛИ. Графическое обозначение этого элемента при двух входных переменных приведено на рисунке 1.la.

Логическое умножение (конъюнкция). Логическая функция у является логическим произведением (конъюнкцией) переменных

x₁, х₂, ..., х_n, если она равна 1 только на тех наборах, на которых все переменные одновременно равны 1. Пример функции у, явля­ющейся логическим произведением двух переменных х₁ и х₂, при­веден в таблице 3.

Логическое умножение двух переменных будем обозначать так же, как обозначают обычное алгебраическое умножение y=x1x2. Для n переменных можно записать:

Y=х₁x₂… x_n (1.3)

а

б

в

г

д

Рисунок 1.1

Схема, с помощью которой из входных переменных х₁, х₂, ..., х_n образуется их логическое произведение у, называется логиче­ским элементом И. Графическое обозначение этого элемента при двух входных переменных приведено на рисунке 1.1б.

Логическое отрицание (инверсия). Логическая функция у яв­ляется логическим отрицанием переменной х, если ее значение противоположно значению переменной х. Функция у, являющаяся отрицанием переменной х, приведена в таблице 1.4. Логическое отрицание принято обозначать Таблица 1.4.

х	у
0 1	1 0

. Схема, с помо­щью которой реализуется логическое отрицание, называется логи­ческим элементом НЕ. Графическое обозначение этого элемента приведено на рисунке 1.lв.

При построении современных цифровых устройств нашли ши­рокое применение некоторые логические функции, являющиеся простыми комбинациями рассмотренных.

Логическое сложение с отрицанием (стрелка Пирса). Логиче­ская функция у является логической суммой с отрицанием незави­симых переменных х₁, х₂, ..., х_n, если она равна 0 на тех наборах, на которых хотя бы одна переменная равна 1. Пример указанной функции при двух переменных приведен в таблице 1.5.

Логическое сложение с отрицанием обозначается .Иногда в литературе пользуются обозначением y=х₁+х₂. В дальнейшем будем использовать первое обозначение. Для функции n переменных можно записать:

Схема, реализующая функцию «логическое сложение с отрица­нием», называется логическим элементом ИЛИ-НЕ (элементом Пирса). Графическое обозначение элемента при двух переменных приведено на рисунке 1.1г.

Логическое умножение с отрицанием (штрих Шеффера). Ло­гическая функция у является логическим произведением с отрицанием

Таблица 1.5 Таблица 1.6

Номер набора	Х2	Х1	У		Номер набора	Х2	Х1	У
0	0	0	1		0	0	0	1
1	0	1	0		1	0	1	1
2	1	0	0		2	1	0	1
3	1	1	0		3	1	1	0

независимых переменных х₁, х₂, ..., х_n, если она равна 1 толь­ко на тех наборах, на которых хотя бы одна переменная равна 0. Пример функции у, являющейся логическим произведением с от­рицанием двух переменных, приведен в таблице 1.6.

Логическое умножение с отрицанием для двух переменных будем обозначать . Иногда в литературе встречается обозна­чение. Для реализации функции «логическое умножение с отрицани­ем» используется логический элемент, называемый элементом И-НЕ (элементом Шеффера). Его графическое обозначение при­ведено на рисунке 1.1д.