УМК по ТВ и МС

Определим теперь, используя базовую таблицу однофакторного дисперсионного анализа, межгрупповую и внутригрупповую дисперсии:

sA2 =

QA

=

4980 =1660,

sε2

=

Qε

=

7270

= 454,38.

n −1

3

n(m −1)

16

В результате имеем фактическое расчетное значение F–отношения

s

2

1660

ψcalc

=

A

=

= 3,65 .

sε2

454,38

Критическое значение F−критерия для уровня значимости α = 0,05 найдем

из таблицы: F5%(3; 16) = 3,24. Поскольку ψcalc > F5%(3; 16), то гипотеза H0 отвергается, т.е. на уровне значимости α = 0,05 различие между партиями сырья оказывает существенное влияние на величину разрывной нагрузки.

10.3. Понятие о многофакторном дисперсионном анализе

Когда на отклик воздействует несколько факторов, может возникнуть необходимость рассмотрения многофакторных моделей. Например, однофакторная модель может оказаться незначимой, если влияние фактора A является несущественным на фоне большого внутригруппового разброса sε. Этот разброс может быть вызван не только случайными причинами, но также действием еще одного «мешающего» фактора B. Фактор B дополнительно включается в модель, чтобы попытаться уменьшить действие неучтенных факторов и повысить влияние на отклик закономерных причин. Аналогично возникает необходимость рассмотрения трех- и многофакторных моделей.

10.3.1. Модель данных при независимом действии двух факторов

Рассмотрим матрицу наблюдений двухфакторного анализа (табл. 10.4). Главный фактор – фактор A, к примеру, влияние настройки станка; дополнительный фактор – фактор B, например, влияние качества сырья. Фактор A принимает n, а фактор B – m различных значений, т.е. n – число станков, m – число партий сырья. Уровни фактора A – способы обработки – отображаются в таблице по столбцам, а уровни фактора B – блоки – по строкам. Это простейшая матрица наблюдений двухфакторного анализа, т.к. в каждой ячейке имеется только одно наблюдение yij. В отличие от однофакторного анализа наблюдения в любом столбце не являются однородными, т.е. не образовывают выборки, если влияние мешающего фактора значимо. Вклады факторов A и B в значения отклика на соответствующих уровнях j и i обозначим через aj и bi. Между факторами нет взаимодействия. Таким образом, каждое наблюдение yij представляется в виде аддитивной модели

yij = bi + a j + εij , (i =1,...,m, j =1,...,n) .

Предполагается, что для случайных величин εij справедливо требование наличия нормального закона распределения N (0, σε2 ) , причем дисперсия σε2 одинакова при всех значениях j и i.

131

Таблица 10.4

	Блоки	Уровни фактора A (способы обработки)
		A1	A2	…	Aj	…	An
	B1B	y11	y12	…	y1j	…	y1n
	B2B	y21	y22	…	y2j	…	y2n
	…	…	…	…	…	…	…
	BiB	yi1	yi2	…	yij	…	yin
	…	…	…	…	…	…	…
	BmB	ym1	ym2	…	ymj	…	ymn

Величины вкладов aj и bi не могут быть восстановлены однозначно. Так, увеличение всех bi и уменьшение всех aj одновременно на одну и ту же константу не изменит значения yij. Для однозначного определения вкладов факторов следует использовать отклонения βi и τj отклика от μ в результате действия

факторов B и A: βi + τj = bi + aj − μ; ∑m= βi = 0, ∑n= τj = 0 , где μ − общая сред-

i 1 j 1

няя значений отклика, ее оценкой является величина y .

Величины β1, … , βm называются эффектами блоков, они характеризуют отклонения от β в результате действия фактора B; τ1, … , τn – эффекты обработки, характеризуют отклонения отклика из-за действия фактора A. Тогда

yij = μ + βi + τ j + εij , (i =1,..., m, j =1,..., n) .

Как и в случае однофакторного анализа, нулевая гипотеза H0 об отсутствии эффектов обработки имеет вид: τ1 = τ2 = ... = τn = 0 .

10.3.2. Базовая таблица двухфакторного дисперсионного анализа при независимом действии факторов

Общая сумма квадратов Q разбивается уже на три части: QA и QB, обусловленные влиянием факторов, и остаточную часть Qε, обусловленную случайной изменчивостью самих наблюдений за счет неучтенных факторов, т.е.

	m	n					n		m	m n
	∑∑( yij − y)2						= m∑( y j − y)2		+ n∑( yi − y)2	+ ∑∑( yij − y j − yi + y)2 ,
	i=1	j=1					j=1		i=1	i=1 j=1
	1442443						1442443		1442443	14444244443
			Q				Q	A	QB	Q
			1							ε
	где y j	=		∑m		yij	– среднее по j-му столбцу, ( y j − y) – оценка эффекта обра-
			m		i=1
	ботки τj;		yi = 1 ∑nj=1 yij – среднее по i-му блоку, ( yi − y) – оценка эффекта
					n

блока βi. Базовая таблица двухфакторного дисперсионного анализа приведена в табл. 10.5.

При выполнении гипотезы H0 об отсутствии эффектов обработки статистики sA2 и sε2 являются несмещенными оценками общей дисперсии σy2. Поэтому для проверки нулевой гипотезы дисперсия по фактору A сравнивается с оста-

точной дисперсией. С этой целью вычисляется F–отношение ψA = sA2 / sε2 ,

132

имеющее F–распределение с n–1, (n–1)(m–1) степенями свободы. На уровне

значимости α гипотеза H0 отвергается, если ψcalc > Fα100% (n −1;(n −1)(m −1)). В этом случае влияние фактора A на отклик значимо.

Таблица 10.5

Источник дис-

Сумма квадра-

Число степеней

Средний квадрат

(оценка диспер-

персии

тов

свободы

сии)

Главные эффек-

Q

B = Q

A

+ Q B

n+m−2

s2

=

QA B

ты

A

B

B

A B

n + m − 2

Фактор A (спо-

QA

2

QA

соб обработки)

n−1

sA

=

n −1

Фактор B

QB

m−1

sB2 =

QB

m −1

Остаточное рас-

2

Qε

сеяние

Qост

(n−1)(m−1)

sε

=

(n

−1)(m −1)

Полная (общая)

B

s2 =

Q

Q = QA B + Qε

−

y

nm 1

nm −1

Аналогично, по F–отношению ψB = sB2 / sε2 проверяется гипотеза об отсутствии влияния фактора B. По F–отношению ψA B = sA2 B / sε2 проверяется значимость двухфакторной модели с независимым действием факторов.

10.3.3. Модель данных при взаимодействии факторов

Мы рассмотрели случай, когда в каждой ячейке матрицы производится одно наблюдение. Анализ выполняется в предположении независимости или аддитивности эффектов столбцов и строк, а также остаточных эффектов. Это аддитивное свойство на практике встречается редко. Предположим, что к некоторой смеси, из которой делается подошва, добавляются два химических вещества. Добавление вещества A увеличивает прочность материала на 8%, вещества B − на 5%. Однако это не означает, что добавление обоих веществ увеличивает прочность подошвы на 13%.

Если между факторами существует взаимодействие, то ему присуща своя дисперсия σ2AB. Без наличия параллельных наблюдений выделить величину σ2AB из общей дисперсии невозможно. Поэтому рассмотрим общую модель, когда в каждой ячейке производится несколько наблюдений. Ограничимся так назы-

ваемыми сбалансированными планами эксперимента, когда в каждой ячейке содержится равное число наблюдений L.

Каждое наблюдение yijl , l = (1,..., L) , представляется в виде

yij = μ + βi + τj + νij + εijl ,

где νij − эффект взаимодействия факторов (i-го уровня фактора B с j-м уровнем фактора A), εijl − вариация внутри ячейки.

Основное тождество двухфакторного дисперсионного анализа примет вид

133

	m n L
	Q = ∑∑∑( yijl − y)2 = QA + QB + QAB + Qε .
	i=1 j=1 l=1
	Оценки дисперсий по факторам имеют прежний вид (табл. 10.5), оценка
	дисперсии взаимодействия факторов sAB2 =			QAB			, оценка остаточной
				(n −1)(m −1)
							Q
	дисперсии sε2 =	Qε	и оценка полной дисперсии sy2		=				.
							nmL −1
		nm(L −1)

Остаточная часть Qε характеризует влияние прочих случайных факторов (кроме факторов A, B и их взаимодействия), она обусловлена наличием не-

m n L

скольких наблюдений в ячейке: Qε = ∑∑∑( yijl − yij )2 .

i=1 j=1 l=1

Значимость влияния факторов A, B и их взаимодействия проверяют по соответствующим F–отношениям (например, ψAB = sAB2 / sε2 ).

Глава 11. Корреляционный анализ

Понятия корреляции и регрессии появились во второй половине XIX в. благодаря работам английских статистиков К. Пирсона и Ф. Гальтона. Для выяснения тех или иных причинно-следственных связей необходимо вести одновременные наблюдения над парой или большим числом случайных величин.

Определение 11.1. Корреляционный анализ – совокупность методов исследования параметров многомерного признака, позволяющая по выборке из генеральной совокупности сделать статистические выводы о мерах статистической зависимости между компонентами исследуемого признака.

11.1. Типы признаков и их классификация

Исследуемые переменные по виду шкалы принимаемых значений подразде-

ляются на количественные, порядковые и классификационные (рис. 11.1).

Количественные признаки измеряются либо в непрерывной шкале, напри-

мер, длина, либо в интервальной или дискретной шкале − когда об их величине судят по попаданию наблюдения в определенный диапазон значений, например, измерение времени при усадке материала с точностью до недели.

Порядковые (ординальные) признаки не поддаются количественной оценке. Реальным содержанием их измерений является тот порядок, в котором выстраиваются объекты по степени выраженности измеряемого признака. На сколько (или, во сколько раз) признак более выражен, не имеет значения, действительны лишь операции типа «больше», «меньше».

Содержанием измерений классификационных (номинальных) признаков яв-

ляются лишь соотношения типа x = c или x ≠ c , x (a, b) или x (a, b) . Взаимный порядок здесь уже не имеет значения. Каждый признак делит группу ис-

134

следуемых объектов на подгруппы. Например, при обработке социологических анкет признак пола разделяет людей на мужчин и женщин; профессия имеет уже большее число наименований.

Рис. 11.1. Классификация основных типов переменных по виду шкалы принимаемых значений и способу измерения статистической связи.

11.2. Виды зависимостей между количественными переменными

11.2.1. Функциональные и статистические зависимости

Обозначим через Y и Xr = (X1,..., X p ) одну и набор случайных величин, за-

висимость между которыми нас интересует. Модель взаимосвязи определяется природой анализируемых переменных, и бывает двух видов.

Функциональные зависимости y = f (x) имеют место при исследовании связей между неслучайными переменными. Выборочные значения y зависят только от соответствующих значений x = (x1, x2, …, xp) и полностью ими определяются. В этом случае в статистических методах нет необходимости.

Статистические зависимости характеризуются тем, что изменение одной из величин влечет изменение закона распределения другой. Они возникают:

1) При исследовании связей между случайными переменными Y и X . В этом

случае величины Y и X зависят от множества неконтролируемых факторов; 2) При исследовании связей между случайными или неслучайными перемен-

ными Y и X , измеряемыми с некоторой случайной ошибкой. В этом случае на-

блюдаются	не сами	переменные, а искаженные, случайные величины
Y′ =Y + εy ,	Xi′ = Xi + εx	, i = (1,..., p) ;
	i

3) При анализе влияния на случайный показатель Y неслучайных факторов X1, X2, … , Xp. Такая связь может быть вызвана двумя причинами:

135

-ошибками измерения показателя Y, по отношению к которым ошибки измерения факторов X1, … , Xp пренебрежимо малы;

-влиянием помимо факторов X1, … , Xp еще и ряда неучтенных факторов.

11.2.2. Типы корреляционных зависимостей

Отметим особый частный случай статистической зависимости – корреляционную зависимость, изучаемую в корреляционном анализе.

Определение 11.2. Статистическая зависимость, при которой при изменении одной из величин изменяется среднее значение другой, называется корреляционной зависимостью.

Корреляционная зависимость может быть представлена в виде
M[Y / x] = M x[Y ] = ϕ(x) или M[X / y] = M y [X ] = ψ( y) ,	(11.1)

где ϕ(x) ≠ const , ψ( y) ≠ const . Уравнения (11.1) называются (модельными) урав-

нениями регрессии соответственно Y по X и X по Y, функции ϕ(x) и ψ(y) − функ-

ции (модели) регрессии, а их графики – (модельными) линиями регрессии.

Основная задача корреляционного анализа – выявление статистической связи между случайными переменными и оценка ее тесноты.

Перед изложением материала остановимся на некоторых «ограничительных» моментах в применении корреляционного анализа.

Американскому писателю О. Генри принадлежит ироническое определение статистики: «Есть три вида лжи − просто ложь, ложь злостная и … статистика!». Попробуем разобраться в причинах, побудивших написать эти слова.

Существо и причины найденной статистической зависимости лежат вне статистических методов. Например, можно обнаружить положительную корреляцию между дозами лекарств и смертностью больных, хотя при очень серьезных заболеваниях смертность увеличивается не из-за больших доз медикаментов, а вопреки им. Корреляционная зависимость может быть обусловлена:

-причинной зависимостью между X и Y;

-общей зависимостью X и Y от третьей величины;

-неоднородностью материала;

-быть чисто формальной (нонсенс-корреляция).

Причинная зависимость существует, например, между талантом и успехом, между временем работы и стоимостью произведенной продукции, между урожайностью сельскохозяйственных культур и погодными условиями.

Причиной корреляции вследствие неоднородности является неоднородный статистический материал, в котором объединены в один показатель различные качественные признаки.

В случае зависимости от третьей величины (совместная корреляция)

найденная корреляционная связь не будет отражать фактической причинной зависимости и приведет к неправильным выводам.

136

В ряду беспричинных корреляций имеется еще формальная корреляция, не находящая никакого объяснения и основанная лишь на количественном соотношении между переменными.

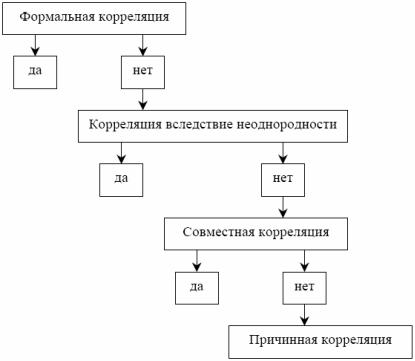
При анализе значимости корреляции можно предложить схему (рис. 11.2), позволяющую выявить истинную корреляцию за счет исключения других возможных зависимостей.

Рис. 11.2. Схема выявления причинной корреляции.

Задача научного исследования состоит в отыскании причинных зависимостей. Только знание истинных причин явлений позволяет правильно истолковывать наблюдаемые закономерности. Однако корреляция как формальное статистическое понятие сама по себе не вскрывает причинного характера связи. Поэтому, при логических переходах от корреляционной связи между переменными к их причинной взаимообусловленности необходимо глубокое проникновение в сущность анализируемых явлений.

11.3. Анализ парных статистических связей между количественными переменными

Рассмотрим зависимость случайной величины Y от одной случайной (или неслучайной) величины X.

11.3.1. Диаграмма рассеяния. Эмпирическая линия регрессии

Двумерная статистическая зависимость может быть наглядно представлена диаграммой рассеяния (рис. 11.3).

137

Рис. 11.3. Диаграмма рассеяния для сгруппированных данных.

Наблюдениями являются парные данные (xi, yi), образующие выборку. Множества значений xi и yi разбиваются на интервалы группировки, границы которых определяют координатную cетку. Каждая пара признаков (xi, yi) изображается в виде точки в соответствующей ячейке. Если в каждом интервале изменения X вычислить средние значения y j , ( j =1,...,5) и соединить соответ-

ствующие точки (x j , y j ) , где x j – середины интервалов, то получим ломаную

линию – эмпирическую линию регрессии, которая в первом приближении характеризует форму связи. По ней можно судить, как в среднем меняется y в зависимости от изменения x. На рисунке связь между X и Y – положительная. Расположение точек относительно линии регрессии характеризует тесноту статистической связи.

Рассмотрим две диаграммы рассеяния 1 и 2, изображенные на рис. 11.4.

Рис. 11.4. Диаграммы рассеяния, отличающиеся теснотой связи между X и Y.

Линии регрессии y по x расположены одинаково, однако точки на диаграмме 2 расположены гораздо ближе к линии регрессии, чем точки на диаграмме 1. Если бы y полностью определялся переменной x, то все точки лежали бы на линии регрессии. При этом каждому возможному значению x было бы поставлено в соответствие определенное значение y, характеризуемое функциональной зависимостью y = f(x). Чем сильнее влияние прочих факторов, тем дальше точки отстоят от линии регрессии. В случае 2 влияние прочих факторов меньше и зависимость между y и x является более тесной.

Если y(x) = const = ay , т.е. линия регрессии – горизонтальная прямая (рис. 11.5), то переменная Y не коррелированна с X.

138

Рис. 11.5. Некоррелированные, независимые случайные величины.

Как было показано в § 4.4, некоррелированность не следует смешивать с независимостью. Случайные величины X и Y независимы, если P( X < x,Y < y) = P( X < x)P(Y < y) . Независимые случайные величины всегда не

коррелированны. Обратное, в общем случае, неверно: переменная Y может зависеть от X, но так, что центры условных распределений не меняются, а изменяются условные дисперсии (на рис. 11.6, диаграмма слева).

Рис. 11.6. Некоррелированные, зависимые случайные величины.

Еще один пример зависимости Y от X, представленный на рисунке, – так называемый «сезонный тренд» (на рис. 11.6, диаграмма справа).

11.3.2. Измерение тесноты парной связи. Коэффициент корреляции

Измерение тесноты связи между переменными позволяет убедиться в ее наличии. Если связь несущественна, то дальнейшие усилия по поиску вида модели зависимости и ее параметров неоправданны.

Рассмотрим важный для практики случай, когда связь между X и Y линейна: y(x) = b0 + b1x . Мерой силы линейной связи признаков X и Y является ко-

эффициент корреляции Пирсона ρ(X,Y), определенный по формуле (2.10).

Ковариация cov(X, Y), а, следовательно, и коэффициент корреляции ρ(X, Y) для независимых случайных величин равны нулю. Однако равенство cov(X, Y) = 0 не означает в общем случае независимости X и Y, т.е. является необходимым, но не достаточным условием для независимости признаков. Величина ковариации зависит от единиц измерения. Поэтому на практике чаще используют коэффициент корреляции, являющийся безразмерной величиной.

Предложение 11.1. (Свойства коэффициента корреляции). Для коэффи-

циента корреляции ρ(X, Y) двух случайных величин X и Y справедливо:

139

1) ρxy не меняется от прибавления к X и Y постоянных слагаемых и от умно-

жения X и Y на положительные числа, т.е. не зависит от выбора начала отсчета и единиц измерения;

2)Если одну из случайных величин умножить на −1, то коэффициент корреляции поменяет знак;

3)−1 ≤ ρ(X, Y) ≤ 1;

4)При ρ(X, Y) = ±1 имеет место линейная функциональная зависимость;

5)Для двумерной нормально распределенной случайной величины из равенства

ρ(X, Y) = 0 следует стохастическая независимость X и Y. #

Замечание 11.1. Величина ρ(X, Y), близкая к ±1, указывает, что зависимость случайных величин почти линейная. Значения ρ(X, Y), близкие к 0, означают, что связь между случайными величинами либо слаба, либо не носит линейного характера, например, является параболической (рис. 11.7).

Рис. 11.7. Параболическая связь

Таким образом, коэффициент корреляции характеризует степень приближения зависимости между случайными величинами к линейной функциональной зависимости. При вычислении выборочного (эмпирического) коэффициента корреляции теоретические величины заменяются их оценками:

		∑n		(xi − x)( yi − y)
rxy =	[∑n	i=1			] [∑n		] .	(11.2)
		(xi	− x)2			( yi − y)2
	i=1				i=1

Если распределение величин X и Y близко к нормальному, то корреляция между ними является линейной и выборочный коэффициент корреляции rxy является надежной оценкой теоретического коэффициента ρ(X, Y). При rxy > 0 связь между переменными положительная, величины X и Y с точностью до случайных погрешностей одновременно возрастают или убывают. Если rxy < 0, то связь отрицательная, с возрастанием одной величины другая – убывает.

Замечание 11.2. Оценка наличия корреляции (11.2) между рядами наблюдений является параметрической, т.к. подразумевает наличие бинормальной генеральной совокупности с параметром ρ, оцениваемым с помощью r.

140