2.4. Случайные векторы; совместная функция и совместная плотность распределения; формула композиции.

Пусть одновременно рассматриваются п случайных величин (ξ₁,ξ₂, …,ξ_п). Они образуют п-мерную случайную величину или п-мерный случайный вектор (или случайную точку в п-мерном пространстве), если задана п-мерная функция распределения F(x₁, x₂, …, x_n) = P{x₁< ξ₁, x₂ < ξ₂, …, x_n < ξп }.

Свойства п-мерной функция распределения:

1. Если среди чисел x₁, x₂, …, x_n есть хотя бы одно равное – ∞ (все остальные - любые), то F(x₁, x₂, …, – ∞, …, x_n) = 0, т.к. { ξ_k < – ∞} – невозможное событие.

2. F(∞,∞, …, ∞) = 1, т.к " k события { ξ_k < ∞} – достоверные.

3. F(x₁, x₂, …, ∞, …, x_n) = F(x₁, x₂, …, x_k–1, x_k+1 , …, x_n); …; F(∞, ∞, …, ∞, x_k, ∞, ∞) = F_k(x_k) = P{ ξk < x_k } – частные функции распределения (п – 1), (п – 2), ..., 2, 1 – мерных случайных векторов.

4. F(x₁, x₂, …, x_n) – неубывающая функция каждого из своих аргументов.

5. F(x₁, x₂, …, x_n) – непрерывна справа по каждому аргументу.

Геометрически функция F(x₁, x₂, …, x_n) определяет вероятность попадания точки в область в п-мерном пространстве, ограниченную плоскостями ξk < x_k , k = 1, 2, …, n. Поэтому, если G – любое измеримое множество n-мерного пространства, то

P{ξ₁, ξ₂ , …, ξп Î G }=.

Если существует

т.е.

то f(x₁, …, x_n) называется п-мерной плотностью вектора (ξ₁,ξ₂, …,ξ_п). Очевидно

,

где все индексы j_ν отличны от i₁, …, i_k, а – плотность вероятности вектора.

Если для всего п-мерного векторного пространства F(x₁, x₂, …, x_n) = F₁(x₁)·F₂(x₂)· …·F_п(x_n), где F_k(x_k) – функции распределения случайных величин – компонент п-мерного случайного вектора, то эти компоненты ξ₁,ξ₂, …,ξ_п называются независимыми случайными величинами. Если существует плотность вероятности п-мерного случайного вектора, то для независимых величин f(x₁, x₂, …, x_n) = f₁(x₁)· f₂(x₂)·…· f_п(x_n) во всём пространстве, причём {f_k(x_k)}, k = 1, 2, …, п – маргинальные плотности случайных величин { ξ_k }.

Плотность вероятности суммы независимых случайных величин называетсякомпозицией (свёрткой) плотностей ,этих величин, что в частном случае двух случайных величин имеет вид:

, (2.12.a)

для непрерывных случайных величин и

(2.12.b)

2.5. Числовые характеристики случайных векторов; характеристики

статистической связи случайных величин

a) Числовые характеристики случайных векторов. Математическим ожиданием случайного вектора (ξ₁,ξ₂, …,ξ_п) называется неслучайный вектор (μ₁,μ₂, …, μ_п), где μ_k = Мξ_k , k = 1, 2, …, п, причём

.

Ковариационной матрицей случайного вектора (ξ₁,ξ₂, …,ξ_п) называется квадратная матрица п-го порядка , элементы которой

–смешанные центральные моменты 2-го порядка двумерных случайных величин (),i, j = 1, 2, …, п, называемах ковариациями пар случайных величин и при i ≠ j, а при i = j представ-ляющих собой дисперсии случайных величин :=D,i = 1, 2, …, п; очевидно . Эти величины надо понимать как:

;

Многомерное распределение называется собственным или невырожденным, если ранг распределения, понимаемый как ранг r матрицы удовлетворяет условиюr = n; при r < n распределение называется несобственным.

Совершенно очевидно, что можно ввести в рассмотрение любые смешанные моменты, как начальные так и центральные, например число

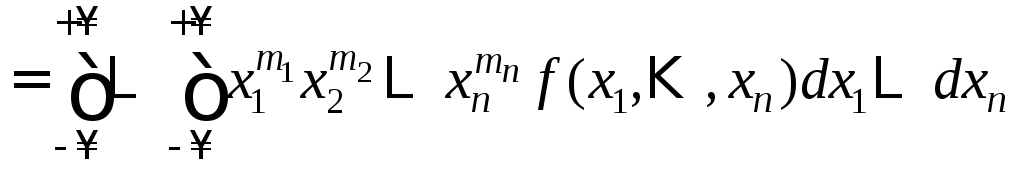–смешанный начальный момент (m₁ + m₂ + … + m_n)-го порядка, а

––смешанный центральный момент (m₁ + m₂ + … + m_n) – го порядка.

Наряду с центральным смешанным моментом порядка (1+1) двумерного случайного вектора, называемого ковариацией, важной групповой числовой характеристикой, отражающей свойства совокупности двух случайных величин, является корреляция :

. (2.13)

для непрерывных и дискретных совокупностей соответственно.

Если случайные величины ξ и η – независимы, то

. Так как при этом

, (2.14)

то ковариация и корреляция случайных величин ξ и η связаны соотношением

cov(ξ,η) = cor(ξ,η) – μ_ξ·μ_η . (2.15)

Очевидно, для независимых величин ξ и η ковариация .

Обратное утверждение в общем случае неверно, т.е. из равенства cov(ξ,η) = 0 в общем не следует независимость случайных величин ξ и η. Такое утверждение, в частности, верно, если случайные величины ξ и η имеют гауссовские распределения.

Легко получить следующие неравенства, задающие верхние и нижние границы корреляции и ковариации:

Если случайные величины ξ и η связаны функциональной линейной зависимостью

η = cξ + b, где c и b – числа, то среднеквадратичное отклонение , а ковариация этих величинчто соответствует граничным значениям её допустимого интервала. Таким образом, ковариация являетсямерой статистической связи между случайными величинами ξ и η, достигая максимального (по модулю) значения при их функциональной линейной зависимости и равной 0 при их независимости. Однако для нелинейной связи между случайными величинами их ковариация не может использоваться как мера статистической связи, поскольку значение ковариации не отражает степень этой связи.

Для характеристики степени статистической связи двух случайных величин ξ и η обычно используют не саму их ковариацию, а коэффициент корреляции этих величин:

ρ(ξ,η) , (2.16)

где случайные величины ξ₀ и η₀ – безразмерные имеют нулевые математические ожидания (Мξ₀ = 0; Мη₀ = 0) и единичные дисперсии (Dξ₀ = 1; Dη₀ = 1) так как получены из исходных величин преобразованием нормировки:

.

Коэффициент корреляции является безразмерной величиной, принимает значения на интервале [-1, 1], и используется как мера статистической связи линейного типа между случайными величинами ξ и η.

Пусть { ξ₁,ξ₂, …,ξ_п } – множество случайных величин. Для каждой пары элементов (ξ_i, ξ_j), i ≠ j, этого множества можно ввести «расстояние» d²() =М(–)² между этими элементами, представляющего собой псевдометрику, что следует из выполнения трёх аксиом, определяющих любую метрику:

1. d(ξ_i, ξ_j) ≥ 0 т.к. М(ξ_i – ξ_j)² ≥ 0, причём из условия (ξ_i – ξ_j) = 0 следует М(ξ_i – ξ_j)² = 0 (если бы было справедливо и обратное то d(ξ_i, ξ_j) было бы метрикой).

2. =, т.к.=.

3. ≤ + т.к..

Для нормированных случайных величин справедливо равенство

Для определения характера статистической зависимости между случайными величинами ξ и η рассматриваются линии регрессии, определяемые равенствами

(2.17)

и представляющие собой средние для y-сечения и x-сечения соответственно. Разумеется, y-сечение представляет собой условное распределение η при заданном ξ = x и его среднее определяет регрессию η по ξ. Аналогично, среднее условного распределения ξ при заданном η = y (x-сечения) определяет регрессию ξ по η.

Если регрессии ξ по η и η по ξ в точности линейны, т. е. имеют место уравнения

, откуда следуют соотношения:

т.е.

(2.18)

– линейные коэффициенты регрессии ξ по η и η по ξ, соответственно. Равенства

(2.19)

называются уравнениями линейной регрессии.

Отношения дисперсий средних значений для x-сечения и y-сечения к дисперсиям величин ξ и η, соответственно, определяют корреляционные отношения ξ по η и η по ξ:

. (2.20)

Так как при строгой линейности одной или обеих регрессий

и/или

, то

, когда обе регрессии линейны; , когда регрессия ξ по η линейна, а η по ξ – нелинейна; аналогично,, когда регрессия η по ξ линейна, а ξ по η – нелинейна. В общем случае, причём корреляционные отношенияне являются мерой ни для какого либо конкретного вида зависимостей случайных величин ξ и η. Лишь значения величин и

могут служить индикаторами (но не мерой) нелинейности.

b) Частная корреляция и регрессия. На практике нередки ситуации, когда корреляция двух случайных величин может быть всего лишь отражением того факта, что они обе коррелированы с некоторой третьей величиной или совокупностью величин. Это приводит к необходимости рассмотрения условных корреляций между двумя величинами при фиксированных значениях остальных величин. Это так называемые частные корреляции.

Пусть{ ξ₁,ξ₂, …,ξ_п } – множество случайных величин; f(x₁, x₂, …, x_n) – их совместная плотность и f(x₁, ..., x_k | x_k+1, …, x_n) – совместная условная плотность распределения, а g(x_k+1, …, x_n) – совместное маргинальное распределение величин{,…,}. Еслиобозначает ковариацию междуив условном распределении величин {ξ₁, …,}, а– их безусловную ковариацию, то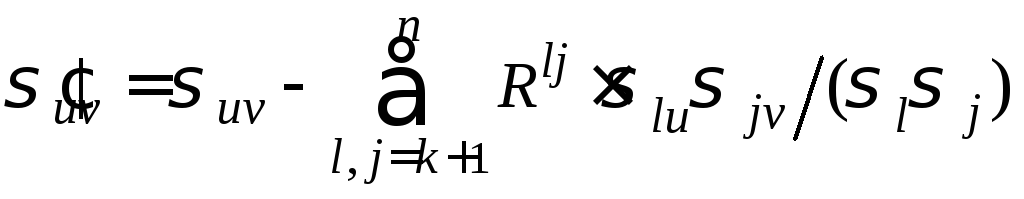, где– корреляционная матрица размера (n – k)× (n – k) величин ξ _{k +1}, …,ξ_п.

Если зафиксировать все переменные, кроме двух, скажем и, точастный коэффициент корреляции между этими величинами равен

, (2.21)

где C_ij – алгебраическое дополнение (i, j)-го элемента в полном (размера n×n) корреляционном определителе , элементы которого связаны с элементами матрицы ковариаций соотношением; величина= {ξ₁, …, ,,…, , ,…, } символизирует совокупность фиксированных величин, а указанныепервичные индексы i, j у q служит для различения таких совокупностей. Частный коэффициент корреляции симметричен относительно переменных, указанными первичными индексами и не зависит явно от фиксированных значений.

В частности, если зафиксировать только одну переменную, например , то = 1 и ; приu= v получаем условную дисперсию u: , гдеи т.п. Тогда частный коэффициент корреляции

. (2.22)

Обобщая понятие линейной регрессии, при рассмотрении п случайных величин следует записать

, где коэффициенты называютсячастными коэффици-ентами регрессии; q_j = (1, 2, …, j–1, j+1, …, n) – набор индексов, определя-ющих совокупность фиксированных переменных. Для многомерного нор-мального распределенияи т.к., то

. (2.23)

Величину

называют ошибкой (остатком) порядка (п–1)величины x_j относительно регрессии. Её дисперсия

. (2.24)

Для многомерного нормального случая . В более общем случае, что применимо и в том случае, когда вторичные индексы одной величины включают в себя первичные индексы другой. Если же оба множества вторичных признаков не содержатl и m, то, обозначив через q общее множество вторичных признаков, получаем

Дисперсию ошибки порядка s можно выразить через дисперсию ошибки порядка (s – 1) и коэффициент корреляции порядка (s – 2) и т.д., вплоть до дисперсии ошибки нулевого порядка и s коэффициентов корреляции, порядок которых принимает значения от нуля до (s – 1):

= (2.25)

где – множество вторичных индексов.

Замечание: порядок вторых первичных и вторичных индексов в приведённом выражении произволен и не влияет на результат.

Формулы для выражения коэффициента регрессии через некоторые коэффициенты следующего, более низкого, порядка и соответствующего частного коэффициента корреляции можно представить в виде:

(2.26)

. (2.27)

c) Множественная корреляция. Используя задаваемую (2.24) дисперсию ошибки случайной величиныотносительно её регрессии, можно ввестимножественный коэффициент корреляции между и совокупностью остальных переменных, множество индексов которых обозначено какq_j:

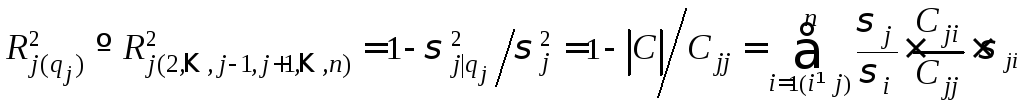. (2.28)

Учитывая (2.23), справедливо выражение

(2.29)

С учётом приведённых соотношений 0 ≤ R² ≤ 1, а сам коэффициент множественной корреляции определяется как корень квадратный из R² и всегда неотрицателен. Коэффициент R, очевидно, несимметричен относительно своих индексов и представляет собой на самом деле меру зависимости от (ξ₁, …, ,,…, ), т.е. являетсяобычным коэффициентом корреляции между и условным математическим ожиданием .

Поскольку в (2.24) допустима перестановка индексов, то из (2.28) следует:

, (2.30)

где – произвольный частный или нулевого порядка (т.е. обычный) коэффициент корреляции (это означает, что множество вторичных индексов (q_j – p) может содержать любое их число от 0 до (n – 2)), содержащий j среди первичных индексов. Таким образом множественный коэффициент корреляции не меньше, чем абсолютная величина любого коэффициента корреляции с таким же первичным индексом, а точнее не меньше наибольшей из корреляций любого порядка.

Пусть q и s – два подмножества вторичных индексов, так что s Í q ( т.е. s – подмножество q). Тогда из (2.24) следует , а с учётом (2.28) справедливы соотношения вида:

, выражающие то, что коэффициент множественной корреляции нельзя уменьшить путём расширения множества величин, относительно которых измеряется зависимость ξ_j. Если множество индексов q = k, т.е. состоит всего из одного индекса то – обычный коэффициент корреляции.