Моменты: . (2.48.B)

Такое распределение имеет вектор ξ = (ξ₁, ξ₂, …, ξ_k), где , где вектор η = (η₁, η₂, …, η_k) имеет k-мерное нормальное распределение с нулевым средним и невырожденной ковариационной матрицей и случайная величина ζ имеет χ² – распределение с n степенями свободы.

Случайная величина , где вектор ξ имеетk-мерное распре-деление Стьюдента с n степенями свободы, вектором сдвига m и матрицей точности, имеет F – распределение сk и n степенями свободы.

Укажем так же распределения Уишарта и Дирихле, как многомерные аналоги χ² – распределения и бета-распределения.

Практическаяработа II

З а д а н и я

Задание 1. (порядковый номер задачи соответствует номеру варианта).

1. Построить ряд распределения, записать функцию распределения, найти математическое ожидание и дисперсию а) числа очков, выпадающих при бросании одной игральной кости; б) суммы очков, выпадающих при бросании п игральных костей.

2. Производится 10 независимых испытаний, в каждом из которых вероятность наступления успеха равна 0,3. Построить ряд распределения, записать функцию распределения, найти математическое ожидание и дисперсию для числа успехов в этих испытаниях.

3. (Геометрическое распределение) Стрелок стреляет в цель до тех пор, пока не поразит её. Вероятность попадания при отдельном выстреле равна р, результаты выстрелов можно считать независимыми. Построить ряд распределения, записать функцию распределения, найти математическое ожидание, дисперсию и среднее квадратичное отклонение числа выстрелов.

4. В урне 10 шаров – 6 белых и 4 чёрных. Шары извлекаются наудачу, без возвращения, до тех пор, пока не появится белый шар. Найти закон распределения, математическое ожидание и дисперсию числа извлечённых при этом чёрных шаров. Построить функцию распределения. Определить вероятность того, что чёрных шаров будет извлечено не менее двух.

5. В партии из 8 изделий имеется одно бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и каждое проверяют. Найти закон распределения, математическое ожидание, дисперсию и среднеквадратичное отклонение числа проверенных изделий. Построить функцию распределения. Определить вероятность того, что будет проверено не менее пяти изделий.

6. Вероятность попадания в цель из орудия при первом выстреле равна 0,5; при втором – 0,7; при третьем – 0,9. Производится три выстрела. Найти закон распределения, математическое ожидание и дисперсию числа попаданий в цель. Построить функцию распределения. Определить вероятность того, будет хотя бы одно попадание.

7. Испытываемая аппаратура содержит 4 блока, отказы которых за некоторое время Т независимы, а их вероятности равны соответственно 0,05; 0,01; 0,07 и 0,02. Найти закон распределения, математическое ожидание и дисперсию числа отказавших за время Т блоков. Построить функцию распределения. Определить вероятность того, что число отказавших блоков будет не более двух.

8. В среднем 9 знаков из 10 передаются по каналу связи без искажения. Построить ряд и функцию распределения числа искаженных (неправильных) знаков в сообщении, состоящем из 5 знаков. Найти математическое ожидание и дисперсию рассматриваемой случайной величины. Оценить вероятность того, что в сообщении, состоящем из 100 знаков, будет ровно 6 искажённых.

9. Построить ряд распределения и функцию распределения F (x) случайной величины ξ – числа выигравших лотерейных билетов, если приобретено 20 билетов, а вероятность выигрыша равна 0,05. Найти математическое ожидание и дисперсию этой случайной величины. Начертить график её функции распределения.

10. В урне 5 белых и 20 чёрных шаров. Вынули один шар. Построить ряд распределения, функцию распределения и начертить её график для случайной величины ξ – числа вынутых белых шаров. Найти математическое ожидание и дисперсию величины ξ.

11. Два стрелка стреляют каждый по своей мишени, делая, независимо друг от друга, по одному выстрелу. Вероятности попадания в мишень для стрелков равны p₁ и p₂, соответственно. Рассмотрим две случайные величины: ξ₁ – число попаданий первого стрелка и ξ₂ – число попаданий второго стрелка. Для случайной величины η = ξ₁ – ξ₂ Построить ряд распределения, функцию распределения и начертить её график; найти математическое ожидание и дисперсию.

12. Производится два независимых выстрела по мишени с вероятностью попадания при каждом выстреле равной р. Для случайной величины ξ, представляющей собой разность между числом попаданий и числом промахов, построить ряд распределения, функцию распределения и начертить её график; найти матожидание Мξ и дисперсию Dξ.

13. Производится ряд независимых опытов, в каждом из которых с вероятностью р может произойти некоторое событие А. Опыты производятся до первого появления события А, после чего они прекращаются. Случайная величина ξ – число произведённых опытов. Построить ряд распределения этой случайной величины и найти её математическое ожидание и дисперсию.

14. Случайная величина ξ принимает значения –1, 0, 1 с вероятностями, равными

0,25; 0,5 и 0,25 соответственно. Написать выражение и построить график функции распределения, найти математическое ожидание и дисперсию величины ξ.

15. Монету бросают п раз. Найти функцию распределения, математическое ожидание и дисперсию случайной величины ξ – числа выпадений герба.

16. Монету бросают до тех пор, пока не выпадет решётка. Найти функцию распределения, математическое ожидание и дисперсию случайной величины ξ – числа выпадений герба.

17. Бросают три монеты. Необходимо задать случайную величину ξ – число выпавших гербов. Построить ряд распределения, функцию распределения и начертить её график; найти математическое ожидание и дисперсию случайной величины ξ.

18. Построить ряд распределения, функцию распределения и начертить её график, найти математическое ожидание и дисперсию для числа попаданий мячом в корзину при двух бросках, если вероятность попадания равна 0,4.

19. Среди 12 лампочек имеется 4 дефектных. Лампочки ввинчиваются в патрон и включается ток. При этом дефектная лампочка сразу перегорает, после чего заменяется новой. Процедура повторяется до тех пор, пока лампочка не будет гореть. Найти закон распределения, математическое ожидание и дисперсию числа использованных лампочек. Написать функцию распределения и начертить её график. Определить вероятность того, что будет использовано более 3 лампочек.

20. На конвейере задействовано п независимо работающих роботов, каждый из которых имеет надёжность (вероятность безотказной работы за время Т ) равную р.

Требуется: а) при п = 4 и р = 0,75 построить ряд распределения, функцию распределения и её график для числа отказавших роботов; вычислить математическое ожидание и дисперсию рассматриваемой случайной величины; б) оценить, при п = 120 и р = 0,95 вероятность того, что за время Т число отказавших роботов будет не менее трёх.

21. Монету бросают п раз. Найти функцию распределения, математическое ожидание и дисперсию случайной величины ξ – отношения числа выпадений герба.к числу выпадений решётки.

22. Случайная величина ξ принимает значения – 2, –1, 0, 1, 2 с вероятностями, равными 0,1; 0,2; 0,2; 0,4; 0,1 соответственно. Написать выражение и построить график функции распределения, найти математическое ожидание и дисперсию величины ξ. Найти вероятность того, что величина ξ примет значение, не превосходящее по абсолютной величине 1.

23. Пусть т – число появлений события А в серии из п независимых испытаний, в каждом из которых Р(А) = р. Величина ξ принимает значения 0 или 1 в зависимости от того, оказались ли т чётным или нечётным. Найти математическое ожидание и дисперсию случайной величины ξ. Для п = 5 для рассматриваемой случайной величины построить ряд распределения, функцию распределения и её график.

24. По мишени, вероятность попадания в которую равна р, ведётся стрельба в неизменных условиях до получения k попаданий. Найти функцию распределения, математическое ожидание и дисперсию числа нужных выстрелов.

25. (Гипергеометрическое распределение) В урне N шаров, из которых п белых. Из урны вынимают т (m<n) шаров. Пусть ξ – число белых шаров среди вынутых. Записать закон распределения и найти математическое ожидание и дисперсию случайной величины ξ. (Указание: при расчёте дисперсии удобно использовать величину Мξ(ξ – 1)).

Задание 2. (номер варианта и исходные данные к нему – по таблице 1)

Дискретная случайная величина ξ может принимать только два значения: x₁ и x₂, причём x₁< x₂. Заданы: вероятность р одного из возможных значений, математическое ожидание Мξ и дисперсия Dξ. Найти: 1) закон распределения этой случайной величины;2) функцию распределения F(x) случайной величины; 3) построить график F(x).

Таблица 1

№ ва- рианта	Рk	Mξ	Dξ	№ ва- рианта	Рk	Mξ	Dξ	№ ва- рианта	Рk	Mξ	Dξ
1	0,1	3,9	0,09	10	0,1	5,5	2,25	19	0,9	2,2	0,36
2	0,5	3,5	0,25	11	0,2	5,8	5,76	20	0,6	4,6	3,12
3	0,3	3,7	0,21	12	0,3	6,6	13,44	21	0,3	9,5	6,72
4	0,7	3,3	0,09	13	0,4	4,4	3,84	22	0,1	7,1	0,78
5	0,2	3,8	0,16	14	0,5	6,0	4,0	23	0,5	7,0	0,5
6	0,8	3,2	0,16	15	0,6	3,0	6,0	24	0,9	1,3	0,63
7	0,4	3,6	0,24	16	0,7	3,8	7,56	25	0,7	4,3	0,78
8	0,6	3,4	0,24	17	0,8	3,4	7,84	26	0,2	7,8	3,46
9	0,9	3,5	0,09	18	0,9	2,8	5,76	27	0,4	5,2	7,44

Задание 3. (номер варианта и исходные данные к нему – по таблице 2)

Случайная величина задана плотностью, которая имеет вид: . Найти:

1) значение коэффициента μ;

2) математическое ожидание, дисперсию, среднеквадратичное отклонение и коффициент вариации;

3) функцию распределения F (x);

4) построить графики f (x) и F (x);

5) вычислить вероятность попадания случайной величины в интервал (α, β).

Таблица 2

№	a	b	c	α	β	№	a	b	c	α	β
1	-3	3	-1	0,5	1,5	16	-2	8	-2	1	3
2	-2	8	-2	1	3	17	-2	4/3	-1/3	1/3	2/3
3	-2	-8	1	-1,5	-1	18	-3	4	-1	-1/3	4/3
4	-2	-8	2	-2	-1,5	19	-4	-6	-2	-0,75	0,25
5	-2	8	-1	1	3	20	-4	6	2	0	0,75

Таблица 2 (продолжение)

№	a	b	c	α	β	№	a	b	c	α	β
6	-4	6	2	0	0,75	21	-3	-4	1	1/3	4/3
7	-2	-4/3	2/3	-1/3	2/3	22	-4	-6	-1	-0,75	0,25
8	-2	-4/3	0	-1/3	2/3	23	-4	6	1	0	0,75
9	-3	3	0	0,5	1,5	24	-3	-4	2	0,5	0,75
10	-3	-3	0	-0,5	1,5	25	-1	4	4	-0,5	0,5
11	-2	8	0	1	3	26	-1	-2	6	0	1
12	-2	-8	0	-1,5	-1	27	-1	-4	-6	-1	1
13	-3	-3	1	-0,5	1,5	28	-1	2	-4	0	3
14	-1	4	-1	0	1	29	-3	-2	3	-2	0
15	-2	2	-3	0	2	30	-4	-4	1	-1	0

Задание 4. (номер варианта и исходные данные к нему – по таблице 3)

Случайная величина ξ задана функцией распределения F(x) или плотностью распределения f (x). Найти: а) найти коэффициенты А и В; б) плотность вероятности f (x) или функцию F(x) ; в) математическое ожидание Мξ, дисперсию Dξ; г) построить графики f (x) и F (x); д) вычислить вероятность попадания случайной величины в интервал (α, β).

Таблица 3

№	F (x) илиf (x)	α	β	№	F (x)	Α	Β
1	Равномерное F (x) =А+В			14	Распределение Рэлея	0	σ
2	F(x) =			15
3	Распределение Коши F (x) =A+B·arctg(x),-∞<x<∞.	-1	1	16
4		0	1	17	f (x) =	0	1
5		0		18
6		0		19	F (x) =A +B(x^2 – x), 1≤ x ≤ 2.	1
7		β	∞	20		0	1
8	Показательное распределение f (x)=	0		21	Распределение Парето	1	2
9		0	1	22	Распределение арксинуса	0

Таблица 3 (продолжение)

10				23		1	∞
11		0	1	24		0
12		0	∞	25		0	а
13	Логистическое распределение	0	β	26	Степенное распределение	0

Задание 5.

По заданному закону или плотности распределения случайной величины ξ найти характеристическую функцию φ(t). Параметры распределений выбрать по вариантам в таблице 4.

Варианты 1 – 5. Биномиальный закон:

Варианты 6 – 10. Закон Паскаля: .

Варианты 11 – 15. Закон Пуассона:

Варианты 16 – 20. Равномерное распределение:

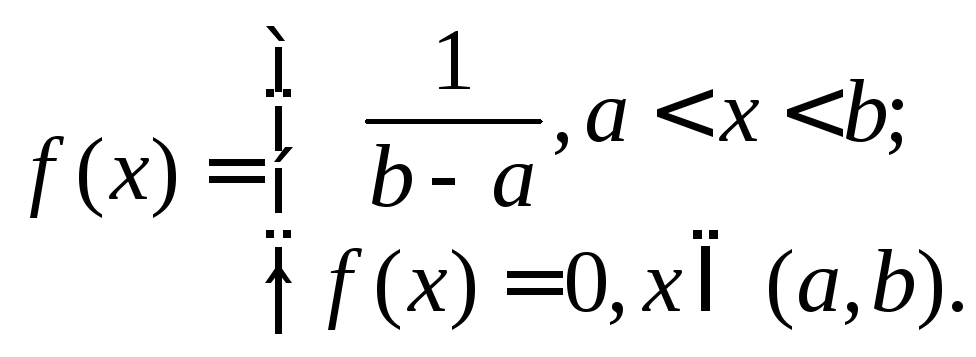
Варианты 21 – 25. Распределение Коши:

Варианты 26 – 30. Гамма-распределение:

Таблица 4.

№ вар.	n	P	a	b	№ вар.	a	b	№ вар.	a	b
1 2 3 4 5 6 7 8 9 10	5 6 7 8 4 – – – – –	0,37 0,53 0,18 0,32 0,25 – – – – –	– – – – – 0,68 0,21 0,72 0,17 0,38	– – – – – – – – – –	11 12 13 14 15 16 17 18 19 20	0,38 0,22 0,82 0,74 0,57 – 4 – 1 2 1 – 3	– – – – – 3 6 4 8 5	21 22 23 24 25 26 27 28 29 30	1 -2 2 -1 1 3,8 2,0 1,8 2,9 4,3	0 1 -1 -2 2 13 5 4 7 10

Задание 6.

Варианты 1 – 5. Случайная величина ξ распределена равномерно в интервале . Найти закон распределения случайной величины η.

Варианты 6 – 10. Случайная величина ξ имеет стандартное нормальное распределение с параметрами (0;1). Найти закон распределения случайной величины η.

Варианты 11–15. Случайная величина ξ имеет распределение Коши:

Найти закон распределения случайной величины η.

Варианты 16 – 20. Случайная величина ξ имеет распределение Рэлея:

. Найти закон распределения случайной величины η.

Варианты 21 – 25. Случайная величина ξ имеет распределение: . Найти закон распределения случайной величины η .

Варианты 26 – 30. Случайная величина ξ имеет показательное распределение

. Найти закон распределения случайной величины η.

Во всех заданиях функциональную зависимость выбирать по таблице вариантов 5.

Таблица вариантов 5

№ варианта	1	2	6, 11, 16, 21, 26	7, 12, 17, 22, 27	3, 8, 13, 18, 23, 28	4, 9, 14, 19, 24,29	5, 10, 15, 20, 25, 30
η	sin ξ	cos ξ	1/ξ	ξ^2	a·ξ + b	exp(-ξ ^2)	|ξ|

Задание 7. (номер задачи соответствует номеру варианта)

1. Случайные величины ξ и η независимы и нормально распределены с М ξ = М η = 0 и

D ξ = D η = σ². Найти плотность вероятности радиус-вектора r = . Приσ =1 найти вероятность того, что случайная точка (ξ ;η) попадёт в кольцо с 2 ≤ r ≤ 3.

2. Случайные величины ξ и η независимы и нормально распределены с М ξ = 2 ;М η = – 3 и D ξ = 4; D η = 9. Написать плотность вероятности и функцию распределения их суммы.

3. Случайные величины ξ и η независимы и распределены по закону Пуассона:

Найти закон распределения их суммы.

4. Двумерная случайная величина (ξ, η) имеет плотность вероятности

Найти: а) величину А; б) функцию распределения F (x, y); в) маргинальные функции распределения F (x) и F (y); г) вероятность попадания случайной точки (ξ, η) в прямоугольник, ограниченный прямыми x = 0, y = 0, x = y = b.

5. По мишени производится один выстрел. Вероятность попадания равна p. Рассмотрев две случайные величины: ξ – число попаданий и η – число промахов, построить функцию распределения F (x, y) двумерной случайной величины (ξ, η). Зависимы ли эти величины?

6. Бросают две игральные кости. Рассмотрев две случайные величины: ξ – число очков, выпавших на первой кости, и η – число очков, выпавших на второй кости , построить функцию распределения F (x, y) двумерной случайной величины (ξ, η), а также функцию распределения F (z) их суммы χ =ξ + η.

7. Два стрелка независимо друг от друга производят по одному выстрелу, каждый по своей мишени. Случайные величины ξ и η – число попаданий первого и второго стрелков, соответственно. Вероятности попаданий в мишени равны p₁ и p₂ для первого и второго стрелков. Построить функцию распределения F (x, y) системы случайных величин (ξ, η).

8. Случайная величина (ξ, η) распределена с постоянной плотностью внутри квадрата, образованного прямыми x = 0, y = 0, x = а, y = b. Записать выражения для совместной плотности распределения f (x, y), а также маргинальных плотностей f_ξ (x) и f_η (y). Определить, являются ли случайные величины: ξ и η независимыми.

9. Система случайных величин (ξ, η) распределена по закону: ; а) найти коэффициент А; б) определить, являются ли случайные величины: ξ и η зависимыми; в) найти вероятность попадания случайной точки (ξ, η) в квадрат, центр которого совпадает с началом координат, а стороны параллельны осям координат и имеют длину а = 2.

10. Случайные величины ξ и η независимы и имеют одно и то же показательное распределение Найти плотность вероятностиих суммы

χ = ξ + η. Определить M χ и D χ.

11. Случайные величины ξ и η, компоненты случайного вектора (ξ, η), имеют следующие характеристики: М ξ = 0 ;М η = 2; D ξ = 2; D η = 1 и коэффициент корреляции . Найти математическое ожидание и дисперсию случайной величины χ = 2ξ – 3η.

12. В готовой продукции брак вследствие дефекта А составляет 3%, а вследствие дефекта В – 4,5%. Годная продукция составляет 95% от общего количества. Найти коэффициент корреляции дефектов А и В.

13. События А и В имеют одинаковую вероятность p. Какова должна быть условная вероятность P(A|B), чтобы коэффициент корреляции между А и В был равен числу r?

14. Случайный вектор (ξ, η) с неотрицательными компонентами (ξ ≥ 0,

η ≥ 0) имеет функцию распределения . Записать маргинальные функции и плотности распределения; Найти математическое ожидание и ковариационную матрицу этого вектора; определить: зависимы или независимы его компоненты.

15. Случайный вектор (ξ, η, ζ) равномерно распределён внутри цилиндра С с центром в начале координат, образующей, параллельной оси oz, высотой 2Н и радиусом основания R Найти распределение каждой проекции этого вектора. Зависимы или нет проекции между собой?

16. Случайные величины ξ₁, ξ₂, …, ξ_{(п + т)}, (n > m) независимы, одинаковы распределены и имеют конечную дисперсию. Найти коэффициент корреляции между суммами и.

17. Случайный вектор (ξ, η) равномерно распределён в квадрате со стороной a и диагоналями, совпадающими с осями координат. Написать выражения для плотностей вектора (ξ, η) и каждой из его компонент. Исследовать случайные величины ξ и η на зависимость и коррелированность.

18. Случайный вектор (ξ, η) равномерно распределён в круге радиуса r с центром в начале координат. Выяснить, зависимы ли и коррелированы ли случайные величины ξ и η. Написать выражения для плотностей каждой из компонент вектора (ξ, η).

19. Случайная величина ξ равномерно распределёна в интервале (0, 2); случайная величина η равномерно распределёна в интервале (–1, 1); ξ и η – независимы. Найти функцию распределения, плотность, математическое ожидание и дисперсию величины ζ = ξ + η.

20. Две точки наудачу брошены на отрезок данной длины a. Положения точек на этом отрезке независимы и равномерно распределены. Найти функцию распределения, плотность, математическое ожидание и дисперсию расстояния между точками.

21. Случайный вектор (ξ, η) равномерно распределён в квадрате с вершинами в точках (0, 0); (0, 1); (1, 1); (1, 0). Найти математическое ожидание и дисперсию случайной величины ζ = ξ · η.

22. Имеются две случайных величины ξ и η, связанные соотношением η = 2 - 3ξ. Известны математическое ожидание и дисперсия случайной величины ξ: М ξ = –1;D ξ = 4. Определить: 1) математическое ожидание и дисперсию случайной величины η; 2) корреляционный момент и коэффициент корреляции величин ξ и η.

23. Имеется система случайных величин (ξ,η,ζ) с заданными характеристиками: математическими ожиданиями Mξ = m_ξ, Mη = m_η, Mζ = m_ζ их ковариационной матрицей

. Найти математическое ожидание и дисперсию случайной величины θ = aξ – bη + cζ – d .

24. Случайная величина ξ распределёна по нормальному закону с математическим ожиданием Mξ = m_ξ и дисперсией Dξ = σ_ξ². Случайные величины η и ζ связаны с ξ сотношениями: η = ξ² и ζ = ξ³. Найти ковариационные моменты cov(ξ,η); cov(ξ,ζ); cov(ζ,η).

Указание: для упрощения вычислений перейти к центрированным величинам.

25. Производится четыре независимых измирения одной и той же величины ξ, причём каждое измерение характеризуется одним и тем же математическим ожиданием Mξ = m_ξ и среднеквадратичным отклонением σ_ξ. Результаты измерений: X₁, X₂, X_3, X₄ очевидно являются случайными величинами. Также случайными величинами будут разности Y₁ = X₂ – X₁; Y₂ = X₃ – X₂; Y₃ = X₄ – X₃. Найти характеристики системы этих случайных величин: математические ожидания ; среднеквадратичные отклонения; нормированную корреляционную матрицу.

26. Тело взвешивают на аналитических весах. Из-за наличия ошибок результат каждого взвешивания X_j (j = 1, 2, …, n, где n – число взвешиваний) случаен и распределяется по нормальному закону с параметрами μ и σ. Истинное (неизвестное) значение веса равно μ. В качестве приближённого значения веса берут среднее арифметическое значение n взвешиваний . Найти: 1) математическое ожидание и дисперсию случайной величины; 2) сколько нужно сделать взвешиваний для уменьшения среднеквадратичной ошибки в 10 раз?

27. Случайная величина ξ принимает значения 1, 2, …, п с вероятностями, убывающими в геометрической прогрессии. Найти зависимость между М ξ и D ξ. Найти P{ξ = n}, если известно, что М ξ = а.

28. Ошибка измерений некоторой величины при одном методе равна 2ξ, где ξ – нормально распределённая случайная величина с Мξ = а, σ = 5; при другом методе измерений ошибка η = η₁ + η₂ – сумма двух независимых нормально распределённых величин, причём

. Какой метод измерений предпочтительнее ?

29. Пусть x₁ и x₂ – результаты двух независимых наблюдений над нормально распределённой случайной величиной ξ. Показать, что где

30. Производится стрельба независимыми выстрелами по некоторой цели до k – го попадания, после чего стрельба прекращается. Вероятность попадания в цель при каждом выстреле равна p; запас снарядов неограничен. Вычислить математическое ожидание и дисперсию числа израсходованных снарядов.

Указание: так как выстрелы независимы и вероятность попадания одинакова, то можно воспользоваться математическим ожиданием и дисперсией числа выстрелов до первого попадания.

Задание 8.

Дан закон распределения двумерной случайной величины (ξ, η) (в виде таблицы). Найти: 1) маргинальные законы распределения компонентов ξ и η; 2) вычислить математические ожидания Мξ = μ₁ ; Мη = μ₂ и средние квадратические отклонения σ₁ ; σ₂ этих величин; 3) условные законы распределения ξ, при условии η = y_j, и η, при условии ξ = x_k, (регрессии ξ по η и η по ξ) а также условные математические ожидания M(ξ | η = y_j) и М(η | ξ = x_k); 4) ковариацию cov (ξ, η) = μ₁₁, коэффициенты регрессии β₁, β₂ и коэффициент корреляции r(ξ, η); 5) уравнения прямых регрессий. В координатах (ξ, η) геометрически изобразить данные таблицы и прямые регрессии.

В а р и а н т ы з а д а н и й

Таблица 6.

8.1						8.2
ξ |η	30	40	50	60	70	ξ | η	5	10	15	20	25
15	0,06					12	0,02
20	0,03	0,05				22	0,04	0,03
25		0,04	0,08	0,05		32		0,05	0,05	0,07
30			0,4	0,07	0,04	42			0,45	0,08	0,04
35			0,02	0,06	0.07	52			0,05	0,02	0,07
40					0,03	62					0,03
8.3						8.4
ξ | η	25	35	45	55	65	ξ | η	11	16	21	26	31
20	0,06					20	0,04
25	0,03	0,05				30	0,02	0,03
30		0,04	0,08	0,05		40		0,06	0,04	0,02
35			0,4	0,07	0,04	50			0,45	0,08	0,04
40			0,02	0,06	0.07	60			0,06	0,06	0,07
45					0,03	70					0,03
8.5						8.6
ξ | η	35	45	55	65	75	ξ | η	4	9	14	19	24
25	0,02					7	0,03
30	0,04	0,06				17	0,03	0,04
35		0,03	0,06	0,02		27		0,05	0,08	0,05
40			0,45	0,08	0,04	37			0,4	0,1	0,03
45			0,04	0,06	0.07	47			0,02	0,06	0,07
50					0,03	57					0,04
8.7						8.8
ξ | η	50	60	70	80	90	ξ | η	7	12	17	22	27
10	0,02	0,02				8	0,04
15	0,02	0,04	0,02			12	0,02	0,07
20		0,05	0,07			16		0,03	0,1	0,07
25		0,06	0,2	0,1		20			0,3	0,1	0,03
30		0,04	0,1	0,1		24			0,05	0,08	0,06
35			0,04	0,06	0,06	28					0,05

Таблица 6 (продолжение).

8.9														8.10
ξ | η	45				55		65	75			85			ξ | η		3			8			13			18			23
10	0,05				0,02									10		0,02
15	0,02				0,05		0,03							20		0,04			0,02
20					0,04		0,1							30					0,06			0,03			0,01
25					0,03		0,35	0,07			0,04			40								0,5			0,1			0,04
30							0,04	0,06			0.07			50								0,02			0,06			0,07
35											0,03			60														0,03
8.11														8.12
ξ | η	10				20		30	40			50			ξ | η		15				20			25			30			35
4	0,02													5		0,04				0,02
9	0,03				0,07									10						0,06			0,04
14					0,03		0,02	0,01						15									0,06			0,45			0,02
19							0,5	0,1			0,04			20									0,02			0,08			0,06
24							0,02	0,06			0.07			25												0,07			0,04
29											0,03			30															0,04
8.13														8.14
ξ | η		20				30	40	50			60			ξ | η		6				12			18			24			30
10		0,02												10		0,03
15		0,06				0,04								14		0,04				0,02
20						0,04	0,07	0,02						18						0,05			0,05			0,07
25							0,35	0,1			0,05			22									0,4			0,08			0,04
30							0,08	0,08			0.06			26									0,05			0,02			0,07
35											0,03			30															0,08
8.15														8.16
ξ | η			18			28	38		48			58		ξ | η			-7			-3			1			5			9
3			0,01											10			0,04			0,07			0,08
8			0,05			0,05								12						0,07			0,08			0,02
13						0,03	0,09		0,04					14						0,05			0,4			0,05
18							0,4		0,11			0,04		16												0,06			0,02
23							0,02		0,06			0.07		18															0,04
28												0,03		20															0,02
8.17															8.18
ξ | η	18			28			38			48			58		ξ | η			-7			-3			1			5		9
-75	0,04														7			0,02
-50	0,06			0,04			0,01								12			0,04			0,08
-25				0,06			0,1			0,05					17						0,02			0,05			0,02
0				0,02			0,25			0,08			0,03		22									0,4			0,08		0,05
25							0,12			0,05			0.07		27									0,05			0,07		0,06
50													0,02		32														0,03

Таблица 6 (продолжение).

8.19													8.20
ξ | η	3		8		13		18			23			ξ | η	10			14			18			22			26
18	0,05												12	0,02
28	0,01		0,03										22	0,04			0,02
38			0,05		0,02		0,06						32				0,06			0,05			0,07
48					0,4		0,11			0,04			42							0,4			0,08			0,04
58					0,09		0,04			0.07			52							0,05			0,02			0,07
68										0,03			62													0,08
8.21													8.22
ξ | η	20		30		40			50			60		ξ | η		15			20			25			30		35
15	0,06												5		0,05
20	0,02		0,04										12		0,01			0,03
25			0,04		0,08			0,02					19					0,05			0,02			0,02
30					0,35			0,1			0,05		26								0,45			0,08		0,04
35					0,07			0,08			0.06		33								0,06			0,06		0,07
40											0,03		40													0,04
8.23													8.24
ξ | η	3		14		25			36			47		ξ | η		-7			-2			2			7		11
5	0,06												-22		0,02
20	0,03		0,05										-12		0,04			0,03
35	0,05		0,07		0,08								-2		0,04			0,05			0,05			0,07
50			0,06		0,4			0,05					8					0,03			0,42			0,08
65					0,02			0,04			0.06		18								0,05			0,02		0,07
80											0,03		28													0,03
8.25													8.26
ξ | η	-13		-4		5			14			23		ξ | η			15			20			25			30	35
-15	0,06												12			0,02			0,04
-10	0,03		0,05										22			0,04			0,03			0,05
-5			0,04		0,08			0,05					32						0,05			0,05			0,07
0					0,4			0,07			0,04		42									0,45			0,08
5					0,02			0,06			0.07		52												0,02	0,07
10											0,03		62													0,03
8.27													8.28
ξ |η		3		24		45			66			87	ξ | η			11			16			21			26	31
15		0,02				0,04							-12			0,02
20		0,03		0,05					0,03				-2			0,04			0,03
25				0,04		0,08			0,05			0,02	8						0,05			0,15			0,07
30				0,07		0,3			0,07			0,02	18						0,02			0,35			0,08	0,04
35						0,02			0,06			0.07	28									0,05			0,01	0,05
40												0,03	38									0,01				0,03

Таблица 6 (продолжение).

8.29						8.30
ξ | η	30	40	50	60	70	ξ | η	-5	0	5	10	15
5	0,04					2	0,02
10	0,03	0,05	0,03			12	0,04	0,03
15	0,02	0,04	0,05	0,04		22		0,05	0,05	0,07
20		0,05	0,35	0,07	0,04	32			0,45	0,08	0,04
25			0,02	0,05	0.07	42			0,05	0,02	0,07
30				0,02	0,03	52					0,03

Задание 9.

По заданному закону распределения найти характеристическую функцию φ(t), кумулянтную функцию γ(t) и первые четыре симиинварианта этого распределения.

В а р и а н т ы 1 – 5: а) биномиальный закон (Бернулли) ;б) .

В а р и а н т ы 6 – 10: а) равномерный закон распределения ;б) гамма-распределение

. (Указание: ) .

В а р и а н т ы 11 – 15: а) закон распределения Пуассона ;б) показатель-ный закон .

В а р и а н т ы 16 – 20: а) закон Паскаля ;б) двойной показательный закон (закон Лапласа) .

В а р и а н т ы 21 – 25: а) геометрический закон распределения (закон Фарри) ;б) нормальный закон распределения с параметрами .

В а р и а н т ы 26 – 30: а) отрицательный биномиальный ;б) равномерное распределение на отрезке [a, b] (в частности на

[-a,a]) .

Решение задач типового варианта.

1. В урне N шаров, из которых п белых. Из урны вынимают т (m<n) шаров. Пусть ξ – число белых шаров среди вынутых. Записать закон распределения и найти математическое ожидание и дисперсию случайной величины ξ.

Решение. В данном случае –гипергеометрическое распределение.

откуда , следовательно

2. Дискретная случайная величина ξ может принимать только два значения: x₁ и x₂, причём x₁< x₂. Заданы: вероятность р = 0,1 одного из возможных значений, математическое ожидание Мξ = 3,5 и дисперсия Dξ = 12,25. Найти: 1) закон распределения этой случайной величины; 2) функцию распределения F(x) случайной величины; 3) построить график F(x).

Решение. 1) Используя определения математического ожидания и дисперсии дискретной случайной величины, составим следующую систему для определения неизвестных x₁ и x₂:

или где положилиp₂ = p = 0,1 и p₁ = 1 – p = 0,9. Таким образом, получаем откуда следует

x₁ = 7/3, x₂ = 14; x₁ = 14/3, x₂ = – 7 и так как по условию x₁< x₂, то x₁ = 7/3, x₂ = 14.

2) Закон распределения данной случайной величины представим в виде таблицы:

i	1	2
xi		14
pi	0,9	0,1

3) Функция распределения имеет следующий вид:

4)

1

0,9

График функции распределения

x

0 14

3. Случайная величина ξ задана плотностью, которая имеет вид: . Найти:

1) значение коэффициента μ;

2) математическое ожидание Мξ, дисперсию Dξ, среднеквадратичное отклонение и коэффициент вариации;

3) функцию распределения F (x);

4) вычислить вероятность попадания случайной величины в интервал (α = 0, β = 1).