
- •Федеральное агентство по образованию
- •Случайное событие
- •Алгебра событий.
- •Элементы комбинаторики
- •Формула полной вероятности.
- •Формула для апостериорной вероятности (формула Байеса)
- •Локальная теорема Лапласа
- •Интегральная теорема Лапласа
- •Случайные величины.
- •Совместное распределение случайных величин.
- •Числовые характеристики случайных величин
- •Математическое ожидание
- •Дисперсия
- •Коэффициент корреляции
- •Функция распределения, ее свойства.
- •Биномиальное распределение
- •Распределение Гаусса.
- •Законы больших чисел.
- •Характеристики выборки.
- •Выборочное среднее, выборочная дисперсия.
- •Гистограмма и полигон
- •Оценка характеристик выборки.
- •Точечные оценки
- •Доверительный интервал. Общее понятие.
- •Доверительный интервал математического ожидания. Случай 1.
- •Распределение
- •Доверительный интервал для дисперсии
- •Распределение Стьюдента.
- •Доверительный интервал математического ожидания. Случай 2.
- •Понятие о теории проверки статистических гипотез.
- •Ошибки при проверке гипотез
- •Проверка гипотезы о функции распределения.
- •Однофакторный дисперсионный анализ
- •Литература
Интегральная теорема Лапласа
Если
вероятность p
появления события A
в каждом испытании постоянна и отлична
от нуля и единицы, то вероятность
![]() того, что событие А появится вn
испытаниях от
того, что событие А появится вn
испытаниях от
![]() до
до![]() раз, приближенно равна
раз, приближенно равна

где
![]() .
.
Для вычислений по формуле имеются таблицы. В таблицах приведены значения функции
![]()
для
положительных значений аргумента.
Значения для отрицательных значений
аргумента вычисляются по формуле
![]() .
.
Случайные величины.
Часто
исход случайного эксперимента выражается
некоторым числом. Когда каждому
элементарному исходу случайного
эксперимента мы ставим в соответствие
некоторое число
![]() ,
мы определяем на множестве событий
некоторую числовую функцию.
Набор чисел может быть конечным или
бесконечным: это зависит от количества
элементарных исходов эксперимента, то
есть от вероятностного пространства.
Неформально говоря, такое число,
принимающее случайные значения, и
называется случайной величиной.
,
мы определяем на множестве событий
некоторую числовую функцию.
Набор чисел может быть конечным или
бесконечным: это зависит от количества
элементарных исходов эксперимента, то
есть от вероятностного пространства.
Неформально говоря, такое число,
принимающее случайные значения, и
называется случайной величиной.
Случайная
величина, принимающая конечное число
значений, называется конечной случайной
величиной.
Пусть пространство элементарных исходов
конечно:
![]() .
Вероятность
.
Вероятность
![]() любого случайного события, связанного
с данным экспериментом, полностью
определяется набором неотрицательных
чисел
любого случайного события, связанного
с данным экспериментом, полностью
определяется набором неотрицательных
чисел
![]()
![]() ,
таких, что
,
таких, что
![]() .
Такое вероятностное пространство можно
представить с помощью таблицы
.
Такое вероятностное пространство можно
представить с помощью таблицы
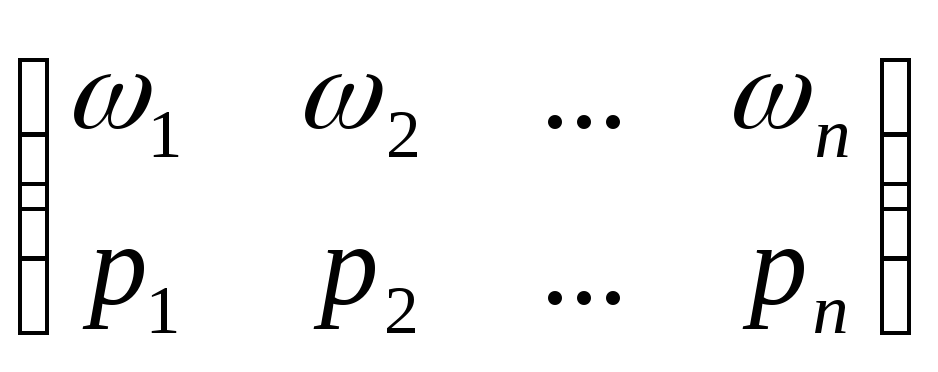
Зададим
случайную величину на таком вероятностном
пространстве. Поскольку число элементарных
исходов конечно, получится конечная
случайная величина. Функцию
![]() ,
заданную на конечном числе аргументов,
также задаем табличным способом:
,
заданную на конечном числе аргументов,
также задаем табличным способом:

Будем
предполагать, что все числа
![]() различны. Случайная величина принимает
значение
различны. Случайная величина принимает
значение
![]() ,
если произошел исход
,
если произошел исход
![]() ,
вероятность которого равна
,
вероятность которого равна
![]() .
Точнее: вероятность события
.
Точнее: вероятность события
![]() равна
равна
![]()
Конечная случайная величина полностью определяется своими значениями и их вероятностями. Поэтому таблица
 ,
,
![]()
часто отождествляется с самой случайной величиной и называется законом распределения конечной случайной величины. Часто закон распределения записывают короче:
 .
.
Совместное распределение случайных величин.
Пусть заданы две конечные случайные величины:
 ,
,

Событие
![]() состоит в том, что одновременно случайная
величина
состоит в том, что одновременно случайная
величина
![]() принимает значение
принимает значение
![]() ,
а случайная величина
,
а случайная величина
![]() - значение
- значение
![]() .
Назовем вероятности таких событий
совместными
вероятностями
и обозначим их через
.
Назовем вероятности таких событий
совместными
вероятностями
и обозначим их через
![]() :
:
![]()
Набор
точек
![]() вместе с совместными вероятностями
вместе с совместными вероятностями
![]() образуют совместное
распределение
случайных величин
и.
образуют совместное
распределение
случайных величин
и.
Две
конечные случайные величины называются
независимыми,
если события
![]() и
и
![]() независимы при всех
независимы при всех
![]() и,
и,
![]() .
В противном случае случайные величины
зависимы.
Для независимых случайных величин
совместное распределение строится по
известным распределениям величин
и:
.
В противном случае случайные величины
зависимы.
Для независимых случайных величин
совместное распределение строится по
известным распределениям величин
и:
![]()
![]() .
.
Пусть заданы две конечные случайные величины:
 ,
,

Их
суммой
называется случайная величина
![]() ,
значениями которой являются всевозможные
суммы
,
значениями которой являются всевозможные
суммы
![]() с
совместными вероятностями
с
совместными вероятностями
![]() .
.
Произведением
этих случайных величин называется
случайная величина
![]() ,
значениями которой являются всевозможные
произведения
,
значениями которой являются всевозможные
произведения![]() с теми же вероятностями
с теми же вероятностями![]() .
.
Числовые характеристики случайных величин
Математическое ожидание
Математическим ожиданием конечной случайной величины

называется число
![]() .
.
Математическое ожидание обладает следующими свойствами.
1. Математическое ожидание постоянной равно ей самой:
![]() .
.
2.
Если случайная
величина принимает только неотрицательные
значения, то
![]() .
.
3. Константу можно выносить за знак математического ожидания:
![]()
4. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
![]() .
.
5. Для любой случайной величины справедливо равенство
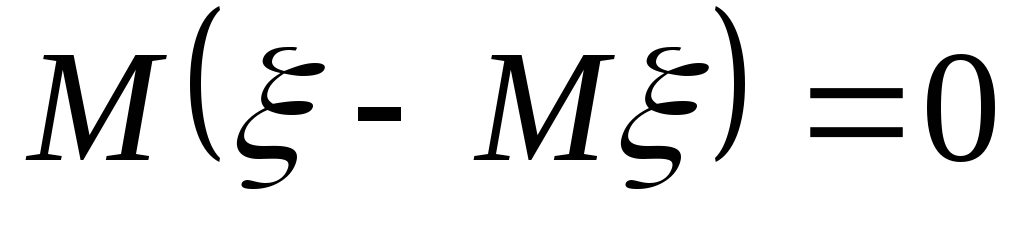 .
.
Операция вычитания математического ожидания из случайной величины называется центрированием.
6. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
![]()
