
- •Федеральное агентство по образованию
- •Случайное событие
- •Алгебра событий.
- •Элементы комбинаторики
- •Формула полной вероятности.
- •Формула для апостериорной вероятности (формула Байеса)
- •Локальная теорема Лапласа
- •Интегральная теорема Лапласа
- •Случайные величины.
- •Совместное распределение случайных величин.
- •Числовые характеристики случайных величин
- •Математическое ожидание
- •Дисперсия
- •Коэффициент корреляции
- •Функция распределения, ее свойства.
- •Биномиальное распределение
- •Распределение Гаусса.
- •Законы больших чисел.
- •Характеристики выборки.
- •Выборочное среднее, выборочная дисперсия.
- •Гистограмма и полигон
- •Оценка характеристик выборки.
- •Точечные оценки
- •Доверительный интервал. Общее понятие.
- •Доверительный интервал математического ожидания. Случай 1.
- •Распределение
- •Доверительный интервал для дисперсии
- •Распределение Стьюдента.
- •Доверительный интервал математического ожидания. Случай 2.
- •Понятие о теории проверки статистических гипотез.
- •Ошибки при проверке гипотез
- •Проверка гипотезы о функции распределения.
- •Однофакторный дисперсионный анализ
- •Литература
Доверительный интервал. Общее понятие.
Пусть
задано число
![]() ,
,
![]() (уровень значимости,
на практике обычно берут,
(уровень значимости,
на практике обычно берут,
![]() или
или
![]() ).
Пусть по выборке удалось построить
интервал
).
Пусть по выборке удалось построить
интервал
![]()
удовлетворяющий равенству
![]() .
.
Случайный
интервал накрывает истинное значение
параметра с заданной, достаточно большой
вероятностью. Найденный интервал не
зависит от значения параметра
![]() .
Тогда интервал
.
Тогда интервал
![]() называют доверительным
интервалом
для параметра
называют доверительным
интервалом
для параметра
![]() с доверительной
вероятностью
с доверительной
вероятностью
![]() .
.
Доверительный интервал математического ожидания. Случай 1.
Дисперсия
![]() известна. Тогда
известна. Тогда![]() ,
если все
,
если все![]() распределены по нормальному закону, то
выборочное среднее тоже имеет нормальное
распределение и
распределены по нормальному закону, то
выборочное среднее тоже имеет нормальное
распределение и
![]()
Доверительный
интервал для математического ожидания
![]() имеет вид
имеет вид
![]() ,
,
где
![]() - квантиль стандартного нормального
распределения,
- квантиль стандартного нормального
распределения,![]() ,
,![]() - уровень значимости.
- уровень значимости.
Распределение
(Читается «ХИ-квадрат»)
П
Рис.
2.
![]() :
- независимые
случайные величины, распределенные по
стандартному нормальному закону:
:
- независимые
случайные величины, распределенные по
стандартному нормальному закону:
![]() .
.
Говорят,
что сумма квадратов этих случайных
величин распределена по закону
![]() с k
степенями свободы.
Эту случайную величину обозначают
с k
степенями свободы.
Эту случайную величину обозначают
![]() :
:
![]()
Запись
![]() также означает, что случайная величина
также означает, что случайная величина
![]() распределена по закону
распределена по закону
![]() с k
степенями
свободы. Графики плотности распределения
с k
степенями
свободы. Графики плотности распределения
![]() при различных k
изображены на рисунке.
при различных k
изображены на рисунке.
Случайная
величина имеет нулевую плотность
распределения при
![]() .
.
При
большом числе степеней свободы k
распределение
![]() близко к нормальному.
близко к нормальному.
Математическое ожидание случайной величины, распределенной по закону k степенями свободы, равно k:
![]()
Доверительный интервал для дисперсии
Теорема.
Случайная величина
![]() распределена по закону
распределена по закону![]() с n-1
степенью свободы
с n-1
степенью свободы
![]()
Если
генеральная совокупность распределена
по нормальному закону и
![]() -
выборочная дисперсия, то доверительный
интервал для дисперсии
-
выборочная дисперсия, то доверительный
интервал для дисперсии
![]() имеет вид
имеет вид
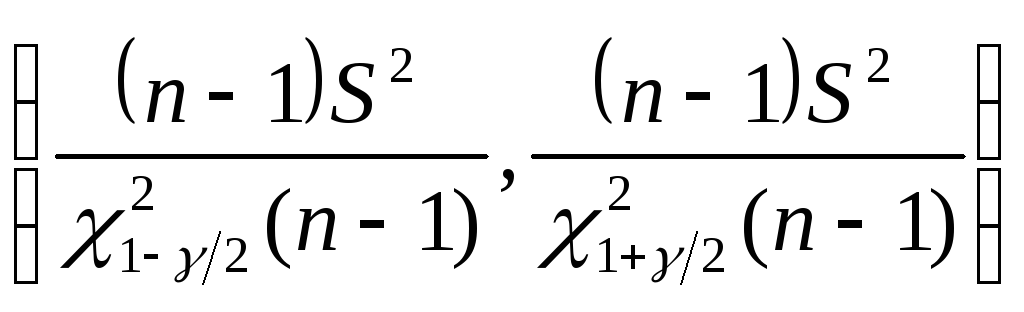
Распределение Стьюдента.
Пусть
случайная величина
![]() распределена по стандартному нормальному
закону:
распределена по стандартному нормальному
закону:
![]() .
Разделим
.
Разделим
![]() на корень из
на корень из
![]() (то есть из случайной величины,
распределенной по закону
(то есть из случайной величины,
распределенной по закону
![]() с k
степенями свободы, деленной на k).
Полученная случайная величина имеет
распределение
Стьюдента с k
степенями свободы. Данная случайная
величина и соответствующий закон
распределения обозначаются через
с k
степенями свободы, деленной на k).
Полученная случайная величина имеет
распределение
Стьюдента с k
степенями свободы. Данная случайная
величина и соответствующий закон
распределения обозначаются через
![]() :
:
![]()
 Рис.
3
Рис.
3
Графики плотности распределения Стьюдента при различном числе степеней свободы приведены на рис. 3. Пунктиром выделено нормальное распределение.
Некоторые свойства распределения Стьюдента.
Распределение Стьюдента симметрично, причем Mt(k) = 0.
При больших k распределение Стьюдента близко к стандартному нормальному распределению N(0,1).
Доверительный интервал математического ожидания. Случай 2.
Если
дисперсия
![]() нормальной генеральной совокупности
неизвестна, то доверительный интервал
для математического ожиданияm
имеет вид
нормальной генеральной совокупности
неизвестна, то доверительный интервал
для математического ожиданияm
имеет вид
![]()
где
![]() - квантиль распределения Стьюдента.
- квантиль распределения Стьюдента.
Понятие о теории проверки статистических гипотез.
Проверяемая
гипотеза называется нулевой
гипотезой и
обычно обозначается![]() .
Наряду с
.
Наряду с
![]() рассматривают альтернативную
(конкурирующую)
гипотезу
рассматривают альтернативную
(конкурирующую)
гипотезу
![]() ,
то есть ту гипотезу, которая будет
принята в случае, если нулевая гипотеза
отвергается. Пусть, к примеру,
рассматривается гипотеза о значении
параметра т
нормальной совокупности:
,
то есть ту гипотезу, которая будет
принята в случае, если нулевая гипотеза
отвергается. Пусть, к примеру,
рассматривается гипотеза о значении
параметра т
нормальной совокупности:
![]() :
:
![]() .
Для этой
гипотезы можно выдвинуть различные
альтернативы:
.
Для этой
гипотезы можно выдвинуть различные
альтернативы:

Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Говорят, что такой подход к проверке статистических гипотез основан на статистическом критерии, или критерии значимости. Построение решающего правила на основе критерия значимости можно разбить на следующие основные шаги.
1.
Сформировать нулевую (![]() )
и альтернативную (
)
и альтернативную (![]() )
гипотезы.
)
гипотезы.
2.
Назначить уровень значимости
![]() .
В качестве уровня значимости обычно
выбирается вероятность того, что нулевая
гипотеза будет отвергнута. Поэтому
.
В качестве уровня значимости обычно
выбирается вероятность того, что нулевая
гипотеза будет отвергнута. Поэтому
![]() - малое положительное число.
- малое положительное число.
3.
Выбрать статистику
![]() критерия для проверки гипотезы
критерия для проверки гипотезы
![]() .
.
4.
Найти плотность распределения статистики
критерия
![]() в предположении, что гипотеза
в предположении, что гипотеза
![]() верна.
верна.
5.
Определить на числовой оси критическую
область
![]() из условия
из условия
![]() (условная вероятность того, что Z
попадает в область
(условная вероятность того, что Z
попадает в область
![]() ,
при условии, что гипотеза
,
при условии, что гипотеза
![]() верна). Область
верна). Область
![]() в этом том случае называется областью
принятия решения.
Условия, задающие критическую область,
называются просто критерием.
в этом том случае называется областью
принятия решения.
Условия, задающие критическую область,
называются просто критерием.
6.
По выборке вычислить выборочное значение
![]() статистки критерия.
статистки критерия.
7. Принять решение:
если,
 гипотеза
гипотеза
 отклоняется (то есть принимается
гипотеза
отклоняется (то есть принимается
гипотеза
 ):
):если
 ,
гипотеза
,
гипотеза
 не отклоняется.
не отклоняется.
Принятое
решение носит вероятностный, случайный
характер. Поэтому обычно применяют
более осторожные формулировки. Вместо
того чтобы сказать "гипотеза
![]() отклоняется, говорят: “данные эксперимента
не подтверждают гипотезу
отклоняется, говорят: “данные эксперимента
не подтверждают гипотезу
![]() ”,
“гипотеза не согласуется с экспериментом”.
”,
“гипотеза не согласуется с экспериментом”.
По поводу предложенной схемы можно заметить следующее.
Значение уровня значимости не определяет критическую область однозначно.
Зная
плотность распределения статистики
![]() ,
можно выделить
сколько угодно областей на числовой
оси, вероятность попадания в которые
равна
,
можно выделить
сколько угодно областей на числовой
оси, вероятность попадания в которые
равна
![]() .
В частности, этому условию удовлетворяют
области
.
В частности, этому условию удовлетворяют
области
![]() ,
,
![]() или
или
![]() ,
где через
,
где через
![]() обозначены квантили распределения
статистики
обозначены квантили распределения
статистики
![]() .
.
Именно эти критические области обычно и применяются. Критерий в этих случаях называют соответственно правосторонним, левосторонним или двухсторонним. На практике выбор критической области обычно определяется видом альтернативной гипотезы.
