
- •Определение цены опциона методом имитационного моделирования
- •Общие принципы имитационного моделирования многокомпонентных систем
- •Организация квазипараллелизма просмотром активностей
- •Два способа изменения (протяжки) системного времени
- •Организация квазипараллелизма транзактным способом
- •Оценка погрешности результирующего показателя имитации из-за различия затравочных чисел генератора псевдослучайных чисел
- •Понижение дисперсии при вычислении интегралов
- •Применение имитационного моделирования (им) к сравнению методов оценивания и анализу их точности
- •Основная литература
- •Дополнительная литература
- •Обобщенный мнк
- •1) Гетероскедастичные ошибки.
- •3. Объясняющие переменные и случайные ошибки одномоментно некоррелированы (хотя в разные моменты и зависимы).
- •Адекватность моделирования. Состоятельные методы
- •Оптимальный предиктор
- •Алгоритм чередующихся математических ожиданий – ace-алгоритм (alternating conditional expectations)
- •Проверка адекватности моделирования
- •Полиномиальная лаговая структура Алмон
- •Геометрическая лаговая структура Койка
- •Модель частичной корректировки
- •Модель адаптивных ожиданий
- •Модель потребления Фридмена
Обобщенный мнк
Необходимо найти
![]() и
и
![]() по заданным z и
по заданным z и
![]() .
.
Сведем ОЛММР к КЛММР.
Известно, что всякая симметричная невырожденная матрица A допускает представление
![]() ,
где C – некоторая
невырожденная матрица. Разложим
,
где C – некоторая
невырожденная матрица. Разложим
![]() .
.
Умножим (1) слева
на C-1:
![]() .
Переобозначим
.
Переобозначим
![]() .
.
Минимизируя
![]() ,
(1*)
,
(1*)
как и ранее, имеем:
![]() и, возвращаясь к исходным наблюдениям:
и, возвращаясь к исходным наблюдениям:
![]() .
(1**)
.
(1**)
Убедимся, что как и в КЛММР:
![]()
![]()
![]() ,
поэтому ковариационная матрица оценок
коэффициентов регрессии по ОМНК:
,
поэтому ковариационная матрица оценок
коэффициентов регрессии по ОМНК:
![]() .
.
Несмещённая оценка
коэффициента![]() :
:
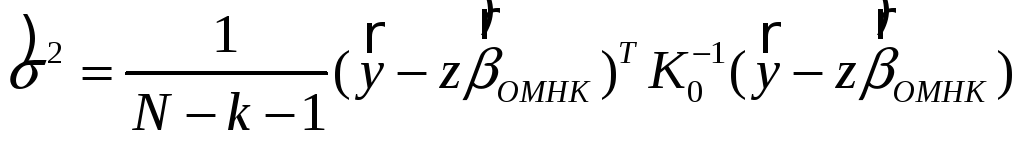 .
.
Коэффициент детерминации:
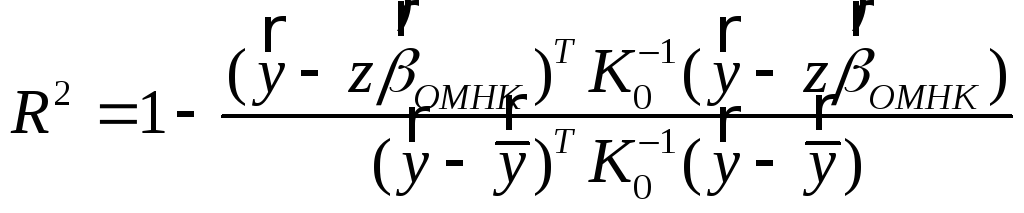 ,
теперь не обязательно
,
теперь не обязательно
![]() ,
имеет вспомогательное, эвристическое
значение.
,
имеет вспомогательное, эвристическое
значение.
Замечание: подставляя в исходный критерий (1*)
![]() ,
получим критерий
,
получим критерий
![]() (2)
(2)
через исходные данные ОЛММР. Решение знаем: (1**).
Замечание:
ситуации, когда
![]() известна, крайне редки (
известна, крайне редки (![]() неизвестных параметров).
неизвестных параметров).
В практически
реализуемом ОМНК приходится вводить
априорные ограничения на структуру
матрицы
![]() (см.
предположения):
(см.
предположения):
1) Гетероскедастичные ошибки.
Подставляя
![]() в (2), получим
в (2), получим
 .
(3)
.
(3)
Поэтому ОМНК в
этом случае называют взвешенным
МНК (![]() –
веса).
–
веса).
Из (3) следует, что
на выработку
![]() более сильное влияние оказывают данные
с меньшей дисперсией ошибок.
более сильное влияние оказывают данные
с меньшей дисперсией ошибок.
Замечание: проверка гипотезы о гомо-/гетероскедастичности ошибок:
![]() (гомоскедастичность);
(гомоскедастичность);
![]() (гетероскедастичность).
(гетероскедастичность).
Разбить выборку
{![]() }
на G кластеров (g
= 1, ..., G) (кластер-анализ).
}
на G кластеров (g
= 1, ..., G) (кластер-анализ).
В каждом кластере найти выборочные дисперсии:
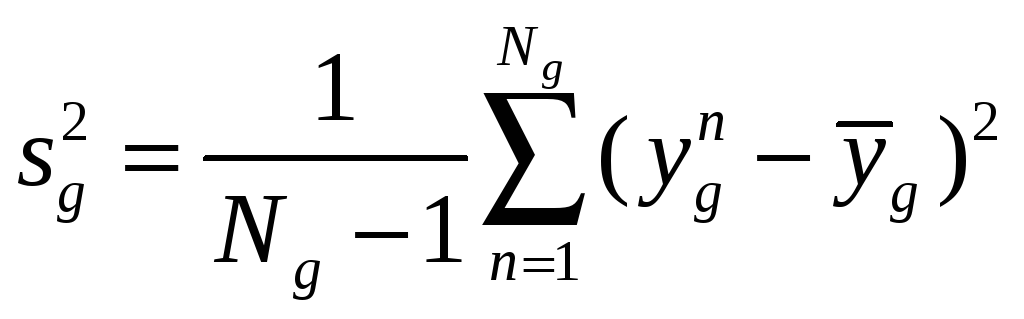 ,
,
где
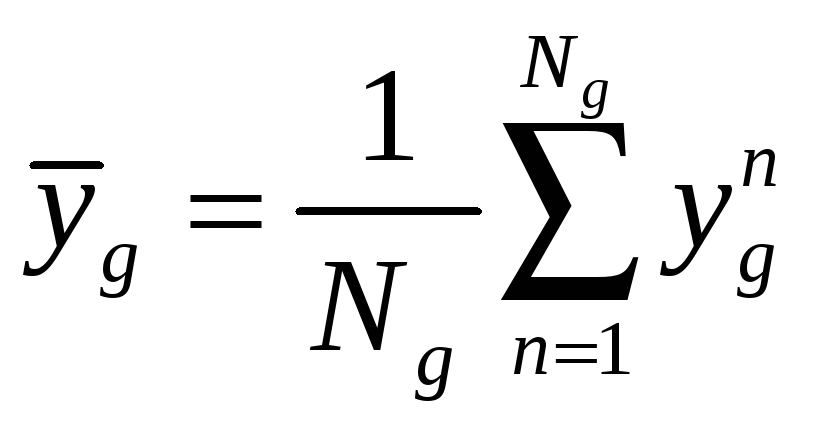 .
.
Затем для проверки
гипотезы
![]() применяется критерий Бартлетта равенства
G дисперсий.
применяется критерий Бартлетта равенства
G дисперсий.
Если
![]() отвергается, то используем ОМНК:
отвергается, то используем ОМНК:
![]() ,
где g – номер
кластера, к которому принадлежит n.
,
где g – номер
кластера, к которому принадлежит n.
2) автокоррелированные ошибки.
Это могут быть, например, ошибки, связанные моделью авторегрессии 1-го порядка (AR(1)):
![]() ,
,
![]() –
белый шум:
–
белый шум:
![]() ,
,
![]() ,
,
![]() –
символ Кронекера.
–
символ Кронекера.
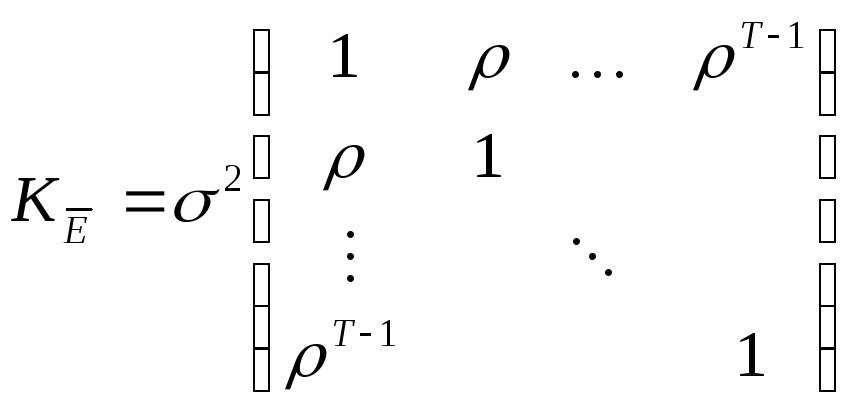 (автокорреляции
затухают с увеличением лага),
(автокорреляции
затухают с увеличением лага),
![]() .
.
Замечание: проверка гипотезы о наличии/отсутствии автокорреляции ошибок (критерий Дербина – Уотсона):
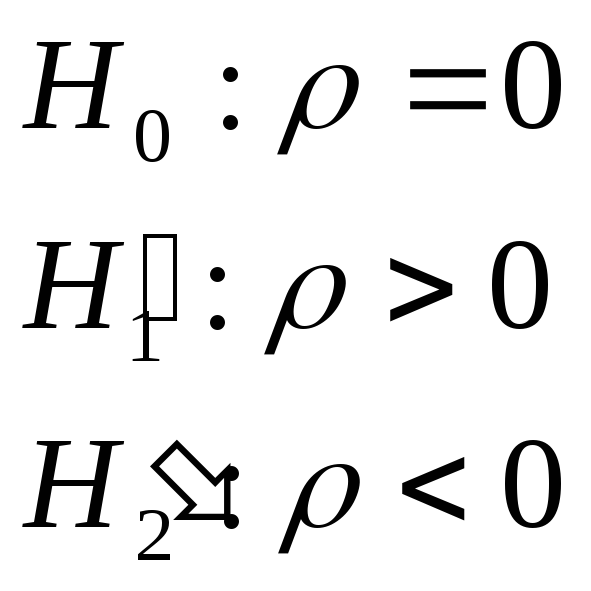
![]() .
.
Статистика критерия:
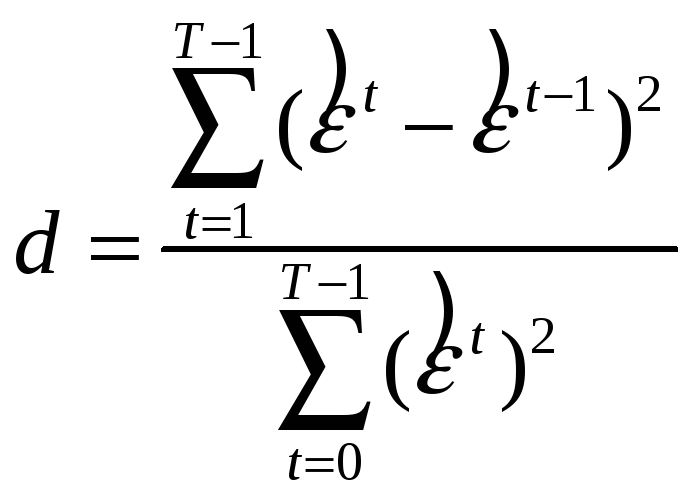 ,
,
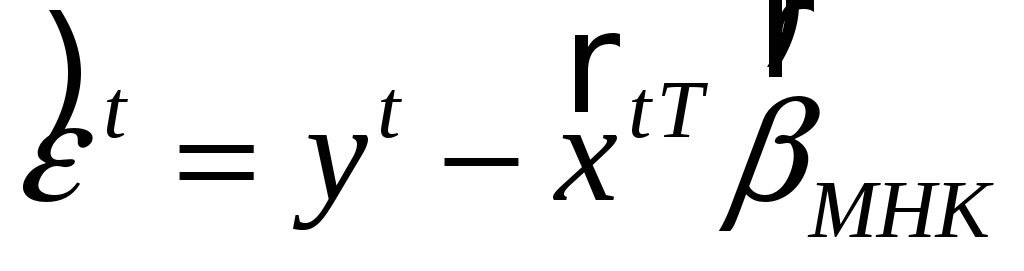 –остатки обычного МНК.
–остатки обычного МНК.
Ясно, что при
![]()
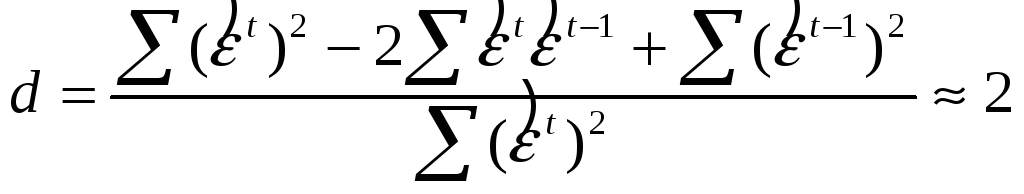 , поэтому, если:
, поэтому, если:
1)
![]() ;
;
2)
![]() .
.
Таким образом,
![]() ?
?
![]()
![]() ?
?
![]()
 | |
| | |
| |
| | |
![]()
![]() 2
2
![]()
![]() .
.
Если автокорреляция
существует, а
![]() неизвестен,
то можно:
неизвестен,
то можно:
а) грубо считать,
что
![]() (и подставить это в
(и подставить это в
![]() );
);
б) использовать процедуру Кохрейна – Оркатта:
– найти
![]() ;
;
–
![]() ;
;
– оценка
![]() находится
как МНК–оценка коэффициента регрессии
в модели
находится
как МНК–оценка коэффициента регрессии
в модели
![]() ;
;
–
![]() ;
;
– переход к п. 2,
где
![]() заменить
на
заменить
на
![]() .
.
Продолжаем цикл
до тех пор, пока
![]() не стабилизируется.
не стабилизируется.
Недостаток алгоритма
состоит в том, что есть опасность уйти
в локальный минимум
![]() .
.
Прогноз в ОЛММР
Оценка нового yN(T) по известным факторам производится по формулам:
1. Гетероскедастичные ошибки:
![]() .
.
2. Автокоррелированные ошибки:
![]() .
.
Дихотомические результирующие показатели. Логит- и пробит-модели
Нередко зависимая переменная – переменная отклика– бинарна по своей природе, т. е. может принимать только два значения. Например, пациент может выздороветь, а может и нет, кандидат на должность может пройти, а может провалить тест при приеме на работу, человек может быть безработным, а может и иметь работу и т. п. Во всех этих случаях нас может заинтересовать поиск зависимости между одной или несколькими “непрерывными” переменными (например, в последнем случае x1 – возраст, x2 – доход за последний год, x3 – стаж работы и т. п.) и одной зависящей от них бинарной переменной.
Конечно, можно использовать стандартную множественную регрессию и вычислить стандартные коэффициенты регрессии. Например, можно задать переменную y со значениями 1’ и 0’, где 1 означает, что соответствующий человек безработен, а 0 – что он занят. Однако здесь возникает проблема: множественная регрессия «не знает», что переменная отклика бинарна по своей природе. Поэтому это неизбежно приведет к модели с предсказываемыми значениями, большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи, таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Задача регрессии
может быть сформулирована иначе: вместо
описания бинарной переменной мы описываем
непрерывную переменную со значениями
на отрезке [0, 1], которую интерпретируем
как вероятность
![]() .
(4)
.
(4)
Здесь
![]() – вектор регрессоров,
– вектор регрессоров,
![]() – вектор коэффициентов регрессии.
– вектор коэффициентов регрессии.
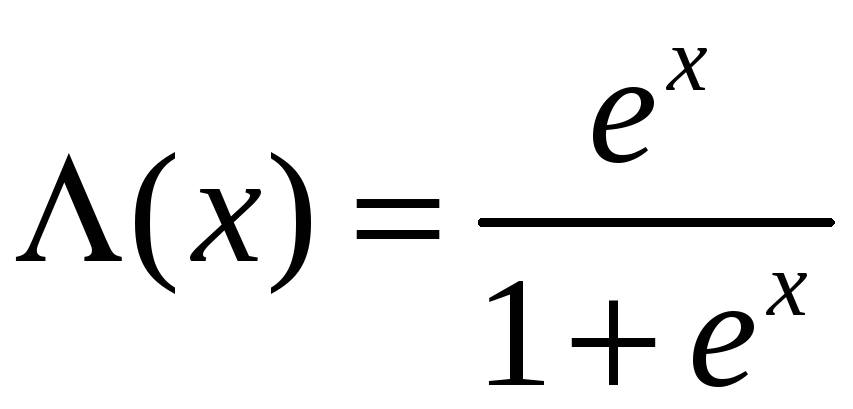 – логистическая
функция.
– логистическая
функция.
Легко заметить,
что вне зависимости от коэффициентов
регрессии и значений
![]() значения p всегда
будут принадлежать отрезку [0, 1]:
значения p всегда
будут принадлежать отрезку [0, 1]:
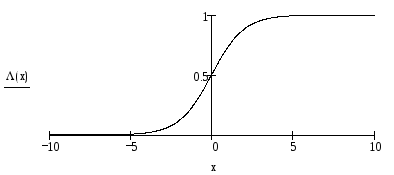
Таким образом, модель логит-регрессии имеет вид
![]() ,
(5)
,
(5)
где En – случайная ошибка в n-м измерении. Очевидно,
En гетероскедастичны,
так как их дисперсия зависит от
![]() .
.
Если вместо
![]() использовать
использовать
![]() – функцию нормального стандартного
распределения, то это будет пробит-модель.
– функцию нормального стандартного
распределения, то это будет пробит-модель.
Модель (5) нелинейна
по параметрам
![]() ,
и перед применением МНК ее следует
линеаризовать. Перенесем ошибку налево
и применим к обеим частям преобразование,
обратное к
,
и перед применением МНК ее следует
линеаризовать. Перенесем ошибку налево
и применим к обеим частям преобразование,
обратное к
![]() .
Ограничиваясь первыми членами разложения
левой части по формуле Тейлора, получим:
.
Ограничиваясь первыми членами разложения
левой части по формуле Тейлора, получим:
![]() ,
,
где
![]() ,
ошибки гетероскедастичны.
,
ошибки гетероскедастичны.
Чтобы при
практическом применении МНК последнее
выражение имело смысл, необходимо
рассматривать группированные или
повторяющиеся данные, заменяя
![]() средним значением, не равным 0 и 1.
средним значением, не равным 0 и 1.
Из-за вышеуказанных трудностей оценку вектора коэффициентов регрессии лучше найти методом максимального правдоподобия. Если вероятность получить 1 есть (4), то вероятность получить 0 есть 1- p и вероятность получить цепочку 1, 0, 0, … есть произведение вероятностей p(1-p)(1-p)….
Функция правдоподобия:
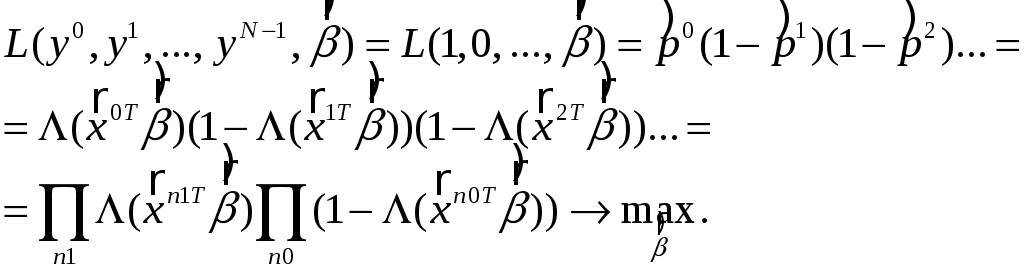
В результате
определяется
![]() такой, что вероятность получить при
имеющихся факторах имеющиеся отклики
будет максимальной. Для проверки качества
моделирования (значимости эффектов
факторов) проверяется гипотеза
такой, что вероятность получить при
имеющихся факторах имеющиеся отклики
будет максимальной. Для проверки качества
моделирования (значимости эффектов
факторов) проверяется гипотеза
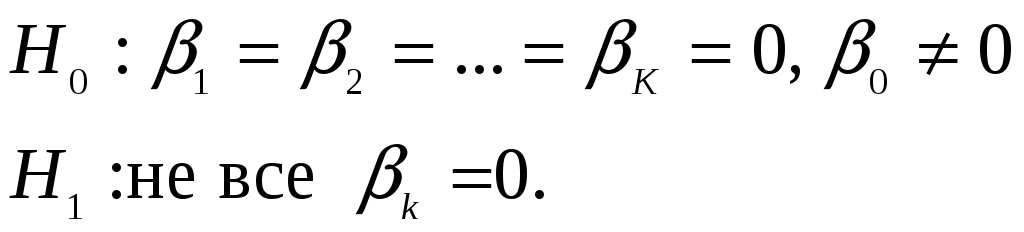
Статистика критерия – логарифм квадрата отношения правдоподобий для моделей H1 и H0 – имеет при H0 приближенно распределение хи-квадрат с K степенями свободы, поэтому уровень значимости:
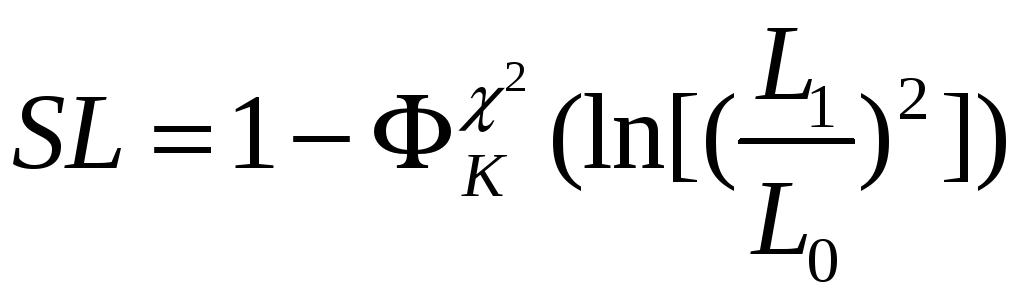 .
.
Маржинальный эффект фактора
Маржинальный эффект фактора xi показывает изменение вероятности
{Y = 1} при изменении фактора xi на единицу.
Можно показать, что он имеет вид:
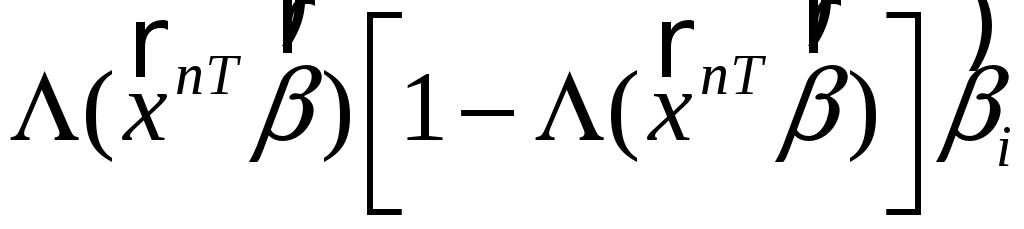 .
.
Пример (продолжение): на сколько процентов увеличится вероятность успеха в задании при увеличении опыта работы (от его среднего значения = 16.88 мес.) на 1 месяц?
Маржинальный эффект = 0.4*0.6*0.161 = 0.038, то есть вероятность успеха повышается на 0.038, или примерно на 10 %.
Стохастические объясняющие переменные
Данная модель имеет вид
![]() ,
(6)
,
(6)
где теперь
![]() –
случайные величины;
–
случайные величины;
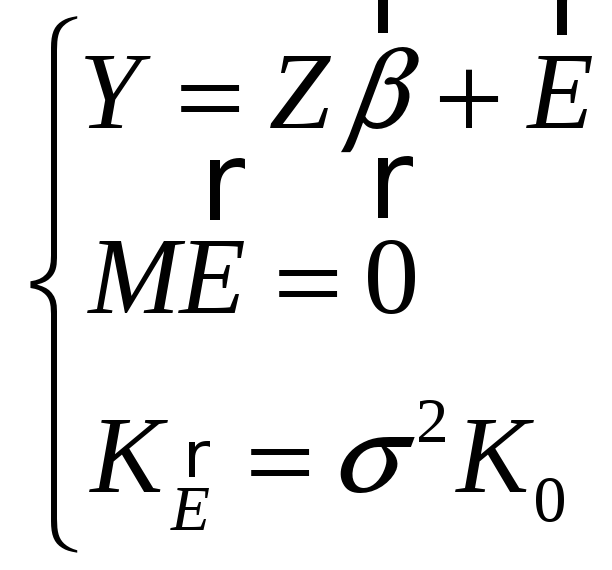
Z – случайная матрица плана.
Рассмотрим три случая.
1. Случайные ошибки
![]() не зависят от
не зависят от
![]() .
.
В этом случае все результаты обычного регрессионного анализа сохраняются. В частности, МНК-оценка остается несмещенной.
Доказательство:
![]()
![]()
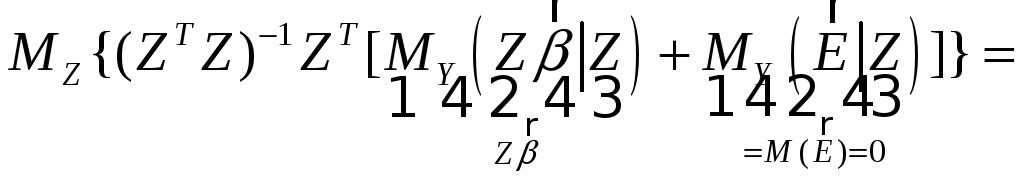
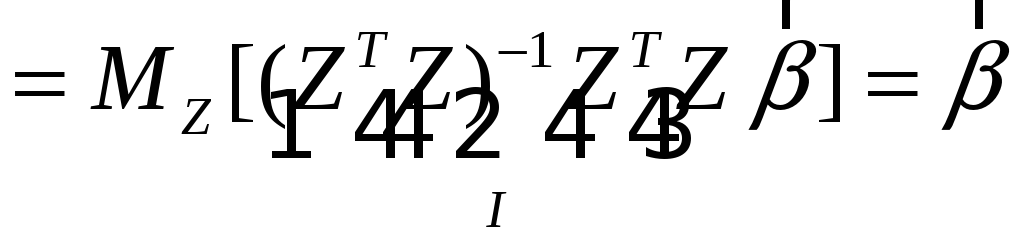 .
.
2. Случайные ошибки
зависят от
![]() .
.
![]() ,
и оценка
,
и оценка
![]() – смещенная и несостоятельная.
– смещенная и несостоятельная.
Метод инструментальных
переменных. Пусть существуют некоторые
переменные
![]() ,
коррелированные с
,
коррелированные с
![]() и
независимые с
и
независимые с
![]() ,
– «инструментальные переменные»:
,
– «инструментальные переменные»:
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() – состоятельная
оценка вектора коэффициентов в (6).
– состоятельная
оценка вектора коэффициентов в (6).
Замечание: аналогичным способом можно было бы “вывести” и обычную формулу МНК-оценки.
Пример (Модель Кейнса):
![]() – потребление в
стране в
– потребление в
стране в
![]() -м
году;
-м
году;
![]() – совокупный
выпуск;
– совокупный
выпуск;
![]() – случайная
особенность
– случайная
особенность
![]() -го
года;
-го
года;
![]() – инвестиции.
– инвестиции.
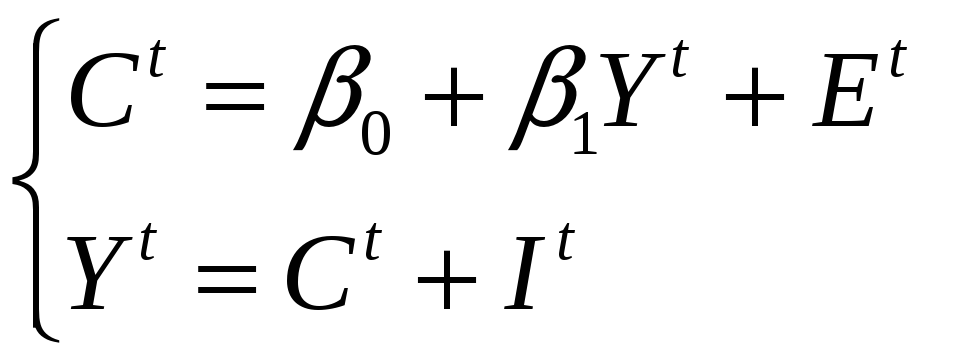 (7, 8)
(7, 8)
(4) –> (5):
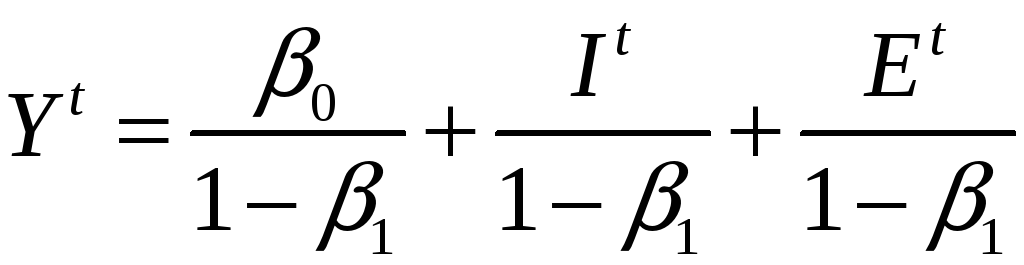 .
.
Видно, что
![]() зависит от
зависит от
![]() ,
поэтому
,
поэтому
![]() ,
оцененная по данным уравнения (7), –
смещенная и несостоятельная.
,
оцененная по данным уравнения (7), –
смещенная и несостоятельная.
Возьмем
![]() в качестве инструментальной переменной:
по (8) она коррелирует с
в качестве инструментальной переменной:
по (8) она коррелирует с
![]() ,
не зависит от
,
не зависит от
![]() ,
т.к. инвестиции – экзогенная переменная,
и определяется другими причинами (может
быть, политическими решениями), нежели
,
т.к. инвестиции – экзогенная переменная,
и определяется другими причинами (может
быть, политическими решениями), нежели
![]() :
:
![]() .
.
Пример: измерения неслучайных переменных (факторов) с ошибками (стохастичность – следствие несовершенных измерений):
![]() .
zn
– не случайны, но, измеряя их, мы получаем
.
zn
– не случайны, но, измеряя их, мы получаем
![]() .
.
![]() –
случайная ошибка измерения;
–
случайная ошибка измерения;
![]() .
.
Поскольку
![]() и
и
![]() зависят от
зависят от
![]() ,
то они зависимы, а значит, обычные
МНК-оценки
,
то они зависимы, а значит, обычные
МНК-оценки
![]() по
по
![]() – смещенные и несостоятельные (см. [2],
с. 248 – 251; [1], с. 729 – 732).
– смещенные и несостоятельные (см. [2],
с. 248 – 251; [1], с. 729 – 732).
