electrodynamics

§6. Квазистационарные токи	121

6.21.Шаровой слой образован концентрическими сферами из идеального проводника, между которыми находится вещество с проводимостью λ. Какое количество тепла выделяется в единицу времени внутри этого слоя, если сферы подключены к источнику постоянного напряжения U0? Внутренний радиус слоя равен R1, внешний – R2.

6.22.Заряженный цилиндрический конденсатор заполнен средой с проводимостью λ и диэлектрической проницаемостью ε. Длина конденсатора –

l, радиусы обкладок – R1 и R2>R1. Найдите зависимость тока утечки от времени, если известно, что в момент t=0 разность потенциалов между обкладками равна U0.

6.23. Пластины плоского воздушного конденсатора, соединенного с источником постоянной ЭДС ε , медленно раздвигают с постоянной скоростью v. Как изменяется со временем сила тока в цепи? Площадь пластин конденсатора S, а расстояние между ними в момент времени t = 0 равно d0.

6.24. Конденсатор переменной емкости состоит из двух прямоугольных металлических пластин, расположенных на расстоянии d друг от друга,

площадь перекрытия которых можно изменять по закону S= t2, перемещая одну из пластин. При этом зазор между пластинами остается неизменным.

Конденсатор соединен с источником постоянной ЭДС ε . Найдите ток в цепи.

6.25. К диаметрально противоположным точкам шара радиусом а, сделанного из плохо проводящего материала с удельным сопротивлением ρ, подключены цилиндрические подводящие провода радиусом r<<a. Найдите сопротивление шара.

122	§7. Магнитное поле квазистационарных токов

§7. Магнитное поле квазистационарных токов

Краткие теоретические сведения

Магнитное поле. Магнитная индукция. Сила Лоренца. Опыт показывает, что движущиеся заряды (например, свободные заряды в проводниках, по которым течет электрический ток) взаимодействуют друг с другом сосвем не так, как неподвижные. Посредником такого взаимодействия является магнитное поле, то есть поле, создаваемое движущимися зарядами и действующее на другие движущиеся заряды.

r

Если частица с зарядом q движется со скоростью v в магнитном поле, то на эту частицу действует сила, носящая название силы Лоренца:

r	r	r	(7.1)
F	= q[v	, B],

r

где B – силовая характеристика окружающего частицу магнитного поля,

которая называется вектором индукции магнитного поля или просто вектором магнитной индукции. Фактически, выражение (7.1) можно считать неявным определением вектора магнитной индукции. Единица измерения магнитной индукции в системе СИ называется тесла (Тл).

Для магнитного поля верен принцип суперпозиции: вектор магнитной индукции поля, созданного системой движущихся заряженных частиц (или проводников с токами), равен сумме векторов магнитной индукции полей, созданных каждой из движущихся частиц (или каждым из проводников) в отсутствие остальных.

Так как сила Лоренца (7.1) в каждый момент времени перпендикулярна скорости заряда, на который она действует, то ее работа при любом перемещении заряда равна нулю. Поэтому магнитное поле не изменяет модуль скорости заряда, но изменяет ее направление.

Закон Ампера. Если проводник с током находится в магнитном поле, то на каждый заряд, образующий этот ток, действует сила Лоренца.

§7. Магнитное поле квазистационарных токов	123

При этом, совокупная сила, действующая со стороны магнитного поля на

r
элемент dl	проводника, определяется законом Ампера:
r	r r
dF	= I [dl , B],			(7.2)
		r
где I – сила тока в проводнике,		B – индукция магнитного поля в точке
расположения рассматриваемого		элемента	проводника, а	направление
r
вектора dl	совпадает с направлением		тока. Чтобы	найти силу,

действующую со стороны магнитного поля на проводник конечной длины,

необходимо проинтегрировать (7.2) по всей длине L проводника:

r	r r
F	= I ∫[dl , B].	(7.3)

L

Сила, определяемая выражением (7.3), называется силой Ампера.

Закон Био-Савара-Лапласа. Чтобы рассчитать силовое взаимодействие проводников с током на основе закона Ампера (7.2), необходимо знать выражение для индукции магнитного поля, создаваемого таким проводником. Для стационарных (не изменяющихся со временем)

токов это выражаение задается законом Био-Савара-Лапласа, который

r

гласит, что вектор магнитной индукции B поля, создаваемого в точке М проводящим контуром L с током I в вакууме, равен

r	r					r		r
		µ		I		[dl , r ]
B(M ) = ∫dB =			0		∫
									,	(7.4)
		4π				r	3
	L				L

где

r r −

r	r
dB	– вклад элемента dl контура в результирующее магнитное поле,
	r	µ		= 4π 10−7	Н/А2 –
вектор, проведенный из элемента dl в точку М, а			0

размерный коэффициент системы СИ, называемый магнитной постоянной. Выражение (7.4) не учитывает запаздывания поля при его распространении от источника до точки наблюдения. В случае достаточно медленно изменяющихся (квазистационарных) токов запаздыванием поля можно пренебречь и применять формулу (7.4) к токам, меняющимся во времени.

В частности, в окрестности бесконечно длинного прямолинейного провода с током I

124			§7. Магнитное поле квазистационарных токов
B =	µ0 I
		,	(7.5)
	2π a

где а – расстояние от провода до точки наблюдения.

Из закона Ампера (7.2) и формулы (7.5) следует, что на отрезок прямолинейного проводника длиной dl с током I1 со стороны магнитного поля бесконечно длинного прямолинейного тонкого провода с током I2, расположенного параллельно первому на расстоянии а от него, действует

сила, равная dF = µ0 2I1I 2 dl . 4π a

Проводники с одинаково направленными токами притягиваются, с противоположно направленными – отталкиваются.

На основе эффекта магнитного взаимодействия токов в системе СИ вводится единица измерения силы тока – ампер. Ампер – сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади поперечного сечения, расположенным на расстоянии 1 метр один от другого в вакууме, вызвал бы между этими проводниками силу, равную

2 10−7 Н на каждый метр длины.

Магнитный момент. Ориентирующее действие магнитного поля. На замкнутый контур L с током I, помещенный во внешнее магнитное поле с

r

индукцией B , согласно закону Ампера (7.2) действует вращающий момент

		r	r	r r
		M	= I ∫[r	[dl , B	]],	(7.6)
			L
где	r	−	вектор,		проведенный из точки,	относительно которой
	r
					r
рассчитывается момент, к элементу контура dl .
		В однородном поле эта формула по правилам векторного анализа
преобразуется к виду
		r	r	r
		M	= [pm , B],			(7.7)
где	p r	−	магнитный момент контура:
	m

§7. Магнитное поле квазистационарных токов		125
r	v
pm	= I ∫dS ,	(7.8)

( S )

v

Здесь элемент dS принадлежит произвольной поверхности S , натянутой на контур, и направлен по правилу буравчика относительно направления протекания тока. Результат интегрирования не зависит от формы поверхности, и потому служит характеристикой контура. Для плоского контура

	v	v
	pm	= IS ,			(7.9)
где S	- площадь контура.
	Под действием момента сил рамка с током стремится занять
устойчивое положение, т.е.			повернуться так, чтобы момент стал равным
нулю.	При	этом вектор	v	становится	сонаправленным с вектором
			pm
	r
индукции B .
	Результирующая сила, действующая на контур с током,
помещенный в однородное магнитное поле,					равна нулю. В неоднородном

r

магнитном поле на контур, помимо момента M , действует отличная от нуля результирующая сила. На контур малых по сравнению с масштабом

неоднородности поля размеров действует сила
r	r	r
		, B),
F = (pm			(7.10)

однозначно определяемая величиной и ориентацией магнитного момента

контура. Контур			втягивается в	область	более	сильного	поля	(если
r	r
	, B)> 0 ),
(pm		либо	выталкивается	в область	менее	сильного	поля	(если

(r r)< pm , B 0 ).

Векторный потенциал. Для удобства вычисления магнитных полей вводится понятие векторного потенциала. Согласно правилам векторного

	r	µ0 I		r
			rot ∫	dl
	анализа выражение (7.4) может быть преобразовано к виду B =				.
		4π
				r
			L
	Поэтому можно ввести векторное поле

126							§7. Магнитное поле квазистационарных токов
r		µ0			r
			∫		Idl
A =						,	(7.11)
		4π
			L		r
такое, что
v			r
B	= rot A .						(7.12)

r

Всякое векторное поле A , удовлетворяющее условию (7.12), называют векторным потенциалом магнитного поля. Его можно определить с точностью до градиента произвольной скалярной функции координат.

Из (7.12), в частности, следует, что
r
div B = 0 ,	(7.13)

то есть магнитное поле соленоидально, причем это свойство остается справедливым и для нестационарных магнитных полей. Силовые линии магнитного поля, как и любого соленоидального, всегда замкнуты.

Векторный потенциал и индукция магнитного поля, создаваемого малым контуром с током, ( т.е. на расстояниях, больших по сравнению с размерами самого контура) так же как и действующие на контур моменты и силы, выражаются (см. Пример 10) через магнитный момент контура и радиус-вектор точки наблюдения, проведенный из центра контура:

		µ0				r	r	]
r	=				[pm		, r
A								,			(7.14)
		4π				r 3
r								r r r	2
		µ0				3(pm , r )r − pm r
B =										.	(7.15)
			4π					r 5

Магнитное поле, создаваемое малым контуром, (элементарным магнитным моментом) во многом аналогично полю точечного диполя в электростатике. Поэтому такой контур называют магнитным диполем.

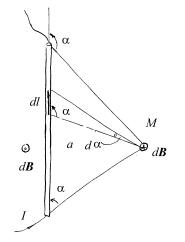
Пример 7.1. Найдите вклад отрезка прямого проводника с током I в магнитную индукцию в точке, отстоящей на расстояние а от проводника,

§7. Магнитное поле квазистационарных токов	127

если прямые, соединяющие эту точку с концами отрезка, составляют с

направлением тока углы									α1 и α2 .
Решение.		r	Выделим					на	проводнике
										r
элемент dl
			, и пусть радиус-вектор r ,
проведенный в точку наблюдения М
из начала этого элемента, образует с
направлением тока угол α, а радиус-
вектор, проведенный из конца этого
элемента		–	угол				α + dα		(см.рис.7.1).
Тогда	из	точки					наблюдения элемент
								dα .		r
виден	под		углом						Вклад	dB
			r
элемента		dl , согласно формуле Био-
Савара-Лапласа,							можно		записать	в
	r		µ	0	I		r r		r
виде	dB	=					[dl ,r	]. Вклады dB		от
			4π r 3
различных									элементов		Рис.7.1
перпендикулярны плоскости рисунка,
							r
а направления							dB	одинаковы в		полуплоскостях,	разделяемых прямой,

r

содержащей проводник. На рисунке слева от этой прямой dB направлены к

нам, что обозначено

на рис.

7.1 кружком с

точкой,

а справа – от

нас

(обозначено символом ).

r

Отсюда следует,

что суммарное поле

B в

точке М перпендикулярно плоскости рисунка. Величина вклада

dB

определяется соотношением

dB =

µ0 Idl sin α

.

(7.16)

4πr 2

Выразим переменные

r и

dl

через постоянную а и переменную α

(см.

a

dB =

µ0 I

рис. 7.1): r = a / sin α ,

dl sin α = rdα =

dα

. Тогда

sin αdα , и

sin α

4π a

следовательно,

128

§7. Магнитное поле квазистационарных токов

α 2

µ0 I

B =

µ0 I

sin αdα =

(cos α − cos α

) .

(7.17)

4π a ∫

2

4π a

1

α

1

В

частности, для

бесконечного

прямолинейного

проводника

α1 = 0,α 2 = π и

B =

µ0 I

,

(7.18)

2π a

r

вектор B в каждой точке пространства лежит в плоскости, перпендикулярной направлению тока; силовые линии представляют собой окружности в этой плоскости с центром на прямой, содержащей проводник.

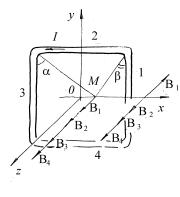
Пример 7.2. По контуру, представляющему собой квадрат со стороной a ,

течет ток I . Найдите индукцию магнитного поля на оси, проходящей через центр квадрата параллельно его стороне.

		Решение.		Существуют				две
	равноправные оси – ось Ох и ось Oy
	системы координат, представленной на
	рис.7.2.	Для	определенности				найдем
				r
	вектор	индукции		B	в	точке		M с
	координатами (x,0).
		Поле,	создаваемое			квадратным
	контуром, можно рассматривать как
	суперпозицию		полей		четырех		отрезков
	прямолинейных			токов.		В		силу
	симметрии		относительно					начала
Рис.7.2	координат ограничимся случаем							x ≥ 0 .
								r

Вклады в результирующий вектор B от каждой стороны квадрата направлены вдоль оси Oz (перпендикулярно плоскости контура) и, следовательно, величина B - есть алгебраическая

§7. Магнитное поле квазистационарных токов	129

сумма этих вкладов. Положительной будем считать проекцию вектора,

направленного по оси Oz (к нам).

Используя решение предыдущей задачи, можно найти индукцию магнитного поля, создаваемого каждой стороной рамки. При 0 < x < a / 2

эти индукции равны:

	B1	=		µ0 I				cos β ,
			2π	(a / 2 − x)
	B	= B		=	µ0 I	(sin α + sin β ),
	2	4			2πa
	B3	=		µ0 I				cosα ,
			2π (a / 2 + x)
	где углы α и β			показаны на рис.7.2.

После несложных преобразований получаем:

a

2

a

2

a

2

a

2

x +

+

x −

+

B =

µ0 I

2

2

−

2

2

πa

x

+

a

x −

a

2

2

.

Если x > a / 2 результат не изменится, хотя направление B1

изменится на противоположное (см. Рис.7.5).

При x >> a последнее выражение можно преобразовать

µ

0

I

1

a

2

1

a 2

B −

1 +

−1 −

=

πa

2 2x − a

2

2x + a

µ0 Ia

1

2

1

2

µ0 Ia

8ax

= −

−

= −

2π

2π

(4x

2x − a

2x + a

2

− a

2

2

)

−

µ

0

Ia

2

= −

µ

0

p

m

,

4πx3

4πx3

130	§7. Магнитное поле квазистационарных токов

где pm = IS = Ia 2 . То есть, при x >> a поле убывает с ростом расстояния,

как поле магнитного диполя с моментом pm = Ia2 .

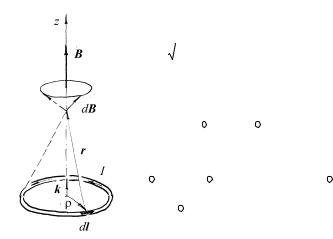
Пример 7.3. По кольцу радиуса

R

течет

ток

I . Найдите

индукцию

r

магнитного поля B в точке, расположенной на перпендикуляре к плоскости

кольца, восстановленном из его центра.

Решение.

Воспользуемся формулой (7.4)

. При

r

интегрировании

по

dl учтем,

что

r =

R2 + z 2

= const

(см. рис. 7.3). Введем

вектор

ρ

так,

что

r

r

r

r

r = kz

− ρ

( k − орт оси Oz).

r

в

(7.4),

получим

Подставив r

µ

I

r

r

r

r

B =

0

{∫[dl , kz]+ ∫[ρ , dl

]}.

Поскольку

вдоль

4πr 3

r

пути

интегрирования

kz = const ,

то

r

r

r

r

r

∫[dl , kz]= [∫dl , kz]=

0 ,

так как ∫dl = 0 .

Кроме

r

r

r

r

r

того,

∫[ρ , dl ]= 2S = 2kS = 2kπR2 . Поэтому

r

µ0 IR

2

r

µ0

r

2 pm

Рис.7.3

B(z ) =

k =

. (7.19)

2(R 2 + z 2 )3 / 2

4π

(R 2 + z 2 )3 / 2

При z >> R из последнего соотношения следует:

B(z ) ≈

µ0 IR2

=

µ0

2 pm

.

2z 3

4π

z 3

Следовательно, при

z >> R

поле убывает с ростом z как поле магнитного

диполя с моментом pm = IS .

В центре

кругового витка (z = 0) магнитная индукция равна

r

r

I

B =

µ0

2 pm

, B = µ

.

4π

R3

0 2R