electrodynamics

§4. Уравнения электростатики

61

зарядов должно остаться прежним, также неизменным должен быть потенциал на границе S области V . Тогда независимо от распределения

зарядов вне области V , поле E внутри нее будет тем же в силу единственности решения задачи о потенциале (рис.4.1) и однозначной связи между E и ϕ .

Пример 4.1. Воспользовавшись первой формулой Грина, докажите возможность приведенной в методе изображений замены поля одной совокупности зарядов полем другой.

Решение. Пусть u(M ) и v(M ) дважды дифференцируемые в области V

функции. Формулу Грина представим в виде

∫(u v + gradu gradv )dV = ∫u		∂v	ds ,	(4.8)
		∂n
V	S
где n - внешняя нормаль к поверхности S .
Положим u = v = ϕ	( ϕ - потенциал			электростатического поля) и

рассмотрим сначала простейший случай, когда объемная плотность заряда в

области V	равна нулю.			Тогда ϕ = 0	и, так как E = − gradϕ , из (4.8)
получим
∫E	2 dV = ∫ϕ	∂ϕ	ds = ∫ϕ E ds .		(4.9)
		∂n
V	S			S
Припишем индекс 1 величинам E и ϕ , относящимся к исходной задаче, а 2
- величинам задачи с				измененными	источниками. Положив в (4.8)

u = v = ϕ1 − ϕ 2 , с помощью приведенных выше рассуждений получим

2				∂ϕ	1		∂ϕ	2
∫(E1 − E2 )	dV = ∫(ϕ1	− ϕ	2 )			−			ds .
							∂n
V	S			∂n

61

62	§4. Уравнения электростатики
Из этого	соотношения видно, что замена исходной задачи	возможна
(E1 ≡ E2	в V ), если удастся изменить заряды вне области V	так, чтобы

выполнялось условие

∫(ϕ1			∂ϕ	1		∂ϕ	2
	− ϕ	2 )			−			ds = 0 .	(4.10)
						∂n
S			∂n
При выборе в качестве поверхности S									эквипотенциальной поверхности,

имеющей для обеих совокупностей зарядов один и тот же потенциал,

условие (4.10) выполняется автоматически.

Если область V содержит заряженные проводники, то объемы,

ограниченные ими, должны быть исключены из V , поскольку на поверхности проводников нормальная проекция вектора D терпит разрыв

(см.(4.7)). В этом случае интеграл в правой части (4.9) вычисляется по

поверхностям S и Si ( i = 1,2,... ), где Si - поверхность i − го проводника.

Учитывая, что на поверхности проводников потенциал остается

постоянным, или ϕ = ϕi , имеем

Si

1

ϕ

ϕ

i

i

∫ϕ E ds = ϕi

−

∫Dn1ds

= −

∫σds = −

qi .

εε

εε

εε

0 Si

0 Si

0

Si

С учетом сказанного условие (4.10) принимает вид

∫(ϕ1

∂ϕ

1

∂ϕ

2

1

∑(q1i

− ϕ

2 )

−

dS

+

− q2i )(ϕ1i − ϕ 2i

) = 0 .

(4.11)

εε 0

S

∂n

∂n

=

i 1

Так как в области V конфигурации заряженных проводников в обеих задачах одинаковы, второе слагаемое в (4.11) также обращается в ноль.

Пример 4.2. Найдите распределение пространственных зарядов, создающее в вакууме поле с потенциалом

§4. Уравнения электростатики											63
		1		1		( 2		2 )		r ≤ R
a			−				− r
						− b R		,	если	.	(4.12)
ϕ (r ) =	r			R
						0				r > R

Решение. Потенциал поля обладает сферической симметрией, поэтому целесообразно выбрать сферическую систему координат, поместив начало

отсчета в точку r = 0 . При r → 0 потенциал имеет особенность: ϕ (r ) → a .

r

Для того чтобы вычленить ее

из

потенциала,

представим

ϕ (r ) в виде

ϕ (r ) =

a

+ ϕ

(r ) , где ϕ

(r )

- всюду непрерывная функция

1

1

r

a

− b(R

2 − r 2 )

−

r ≤ R

ϕ1 (r ) =

R

a

,

если

.

(4.13)

−

r > R

r

Особенность потенциала (4.12) в окрестности r = 0 того же типа, что и

особенность поля точечного заряда, помещенного в эту точку. Из формулы

для потенциала точечного заряда имеем

q

=

a

. Откуда

4πε 0 r

r

q = 4πε 0 a .

(4.14)

Согласно (4.7) на заряженных поверхностях нормальная

составляющая вектора

D терпит разрыв. Используя соотношения (4.3) и

(4.4), а также симметрию задачи, находим

E = −n

dϕ1

,

D = n

D , где

r

1

dr

1

r 1

nr = r / r и

− 2bε 0 r

r < R

aε 0 ,

D1 =

если

.

(4.15)

−

r

> R

r

2

Откуда

63

64 §4. Уравнения электростатики

				a
σ = lim D(r )− lim D(r ) =			−			+ 2bR ε	0 .	(4.16)
					2
r →R	r →R			R
+	−

Объемную плотность заряда можно найти, используя уравнение

(4.5), которое в сферической системе координат для поля, зависящего

только от r , принимает вид

1

d

2

dϕ

1

ρ

ϕ

=

r

= −

.

1

r 2

dr

dr

ε 0

Подставляя сюда ϕ1 из (4.13), получаем выражение для объемной плотности заряда:

− 6bε 0			,	если	r < R			(4.17)
ρ =					.
	0				r > R
Итак, потенциал (4.12) создается следующей конфигурацией
зарядов:
а) точечным зарядом q (4.14), расположенным в точке r = 0 ;
б) равномерно		заряженной			сферой радиусом	R	с	поверхностной
плотностью заряда σ (4.16);
в) равномерно заряженным по объему шаром радиусом								R с объемной
плотностью ρ (4.17).
Распределение потенциала (4.12) позволяет утверждать, что полный
заряд системы равен нулю. Действительно, при r > R							согласно (4.4)		поле
отсутствует и D = 0 . Используя теорему Гаусса для						сферы		радиуса r	> R
с центром в точке r = 0 , получим, что заряд внутри сферы равен нулю.
Если	b =	a		, то, как видно из (4.16), плотность поверхностного
		2R 3

заряда равна нулю, и точечный заряд q компенсируется объемным зарядом шара.

§4. Уравнения электростатики

65

Пример 4.3. Точечный заряд q расположен на расстоянии h от бесконечной

проводящей заземленной плоскости. Найдите силу F , действующую на

заряд, и поверхностную плотность σ индуцированного на плоскости заряда.

Решение. Воспользуемся методом электростатических изображений.	В
качестве области V , в которой поля заданной и модельной конфигураций
зарядов будут совпадать, выберем полупространство z > 0 , где	ось
0z направим перпендикулярно плоскости проводника через заряд q	(см.

рис.4.1а), а на плоскости выберем полярную систему координат ( ρ ,ψ ). Так как поле точечного заряда убывает с возрастанием расстояния от него, то модуль плотности заряда, индуцированного им на плоскости, будет убывать с ростом ρ .

Уберем плоскость с наведенным на ней зарядом и подберем вне V

(в полупространстве z < 0 ) систему зарядов такую, чтобы потенциал

плоскости был равен нулю. Нетрудно убедиться в том, что поместив заряд

−q

в точку

на

оси

0z

с

координатой

z = −h (отражение

заряда

q

плоскостью

z = 0 ), получим,

что потенциал плоскости симметрии z = 0

равен нулю (см. рис.4.1б). Следовательно, поле

E1

исходной задачи для

z > 0 эквивалентно полю

E2 , создаваемому зарядом q

и отраженным

зарядом −q .

С учетом сказанного сила взаимодействия заряда

q с плоскостью

равна силе взаимодействия между зарядом

q и его «отражением» −q :

F =

q 2

и

является

силой

притяжения,

а

потенциал

поля

в

16πε

0

h 2

произвольной точке области V

ϕ1 =

ϕ 2 =

q

−

q

.

4πε 0

ρ 2 + (h − z )2

4πε 0

ρ 2 + (h + z )2

Для определения поверхностной плотности наведенного на плоскости заряда воспользуемся граничными условиями (4.7) и связью между потенциалом и напряженностью поля (4.4):

65

66 §4. Уравнения электростатики

σ (ρ ) = Dn	= −ε		∂ϕ1		= −	qh
		0					.
			∂z		z = 0	2π (ρ 2 + h 2 )3 / 2

Для определения суммарного заряда, индуцированного на плоскости,

следует подсчитать интеграл

∞		qh		∞	dρ 2
Q = ∫	σ (ρ ) 2πρdρ = −			∫		= −q .
					3 / 2
0	2		0		(ρ 2 + h 2 )
Пример 4.4.	Точечный заряд		q		находится на расстоянии		a (a > R) от
центра проводящей сферы радиусом R . Заряд сферы равен							Q . Найдите
силу, действующую на заряд q .

Решение. Воспользуемся методом электростатических изображений. В

качестве области V выберем пространство вне сферы, содержащее заряд q . Внутри проводящей сферы E = 0 , а потенциал остается постоянным и

равным потенциалу центра сферы ϕ 0 , который согласно принципу суперпозиции равен

q

σds

1

1

1 q

Q

q

ϕ 0 =

+ ∫

=

+

∫σds

=

+

.

4πε

4πε

4πε

a

R 4πε

a R

a R

0

0

0

0

Здесь σ − поверхностная плотность заряда Q, неравномерно

распределенного по сфере.

Уберем теперь заряженную сферу и

подберем систему зарядов вне V

(внутри

сферы) так, чтобы потенциал на ее

поверхности

сохранил прежнее

значение.

Эту задачу решим в два этапа. На первом

этапе выберем заряд q' так,

чтобы

потенциал сферы стал равен нулю. Для этого

можно воспользоваться решением примера 9	Рис.4.2

§4. Уравнения электростатики	67
параграфа 2: для двух точечных зарядов q и q'	поверхностью нулевого

потенциала является сфера, центр которой лежит на прямой, соединяющей

заряды.

Допустим,

что искомый заряд

q' находится на расстоянии x от

центра сферы, тогда из условия ϕ A = ϕ B = 0 (см. рис.4.2) имеем

1

q

q'

ϕ A

=

+

= 0

и

4πε

0 a − R R − x

1

q

q'

ϕ B

=

+

= 0 .

(4.18)

4πε

0 a + R R + x

Решая систему уравнений (4.18), определяем q' и x

q' = −q

R

x =

R 2

,

.

(4.19)

a

a

На втором этапе подберем заряд q' ' так, чтобы потенциал сферы

принял

значение

потенциала

исходной

задачи. Очевидно, что заряд q' '

следует поместить в центр сферы. Учитывая, что суммарный вклад в потенциал сферы зарядов q и q' равен нулю, получим

ϕ 0 =

q' '

4πε 0 R

Откуда q' ' =

	1		q				Q
=						+		.
	4πε	0 a					R
Q + q		R		.			(4.20)
		a

Таким образом поле E исходной задачи в области V

эквивалентно полю,

создаваемому зарядами q, q'

и q' ' . Сила,

действующая на заряд q , согласно

q

q'

принципу суперпозиции равна

F =

+

q' '

.

4πε

(

)2

a

2

0

a − x

Подставляя выражения для

x, q' и q' ' ,

полученные выше, окончательно

находим

67

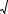
68

§4. Уравнения электростатики

q 2

Q

R 3

(2a 2

− R 2 )

F =

−

.

(4.21)

a(a

4πε 0 a

2

q

2

− R

2 2

)

Анализ полученного результата удобнее провести, представив (4.21)

в виде

F =

q

2

Q

− f (ξ ) .

0 a 2

4πε

q

Здесь ξ =

R

и

f (ξ ) = ξ

3

2 − ξ 2

.

(1 − ξ 2 )2

a

Так

как 0 < ξ < 1 ,

то

f (ξ ) > 0

и

функция

f (ξ ) монотонно

возрастает,

причем 0 < f (ξ ) < ∞ .

Если заряды q и Q разноименные, то F < 0 при любом ξ , то есть

заряд q притягивается к сфере.

Если заряды q

и Q одноименные, то уравнение f (ξ ) =

Q

имеет

q

единственное

решение

ξ 0 , определяющее положение

a = a0

заряда

q

( a0

=

R

), при котором

F = 0 .

Если

a > a0

( ξ < ξ0 ),

то F > 0 , то есть

ξ 0

заряд q отталкивается от сферы;

при a < a0

( ξ > ξ0 )

F < 0

и заряд

q1

притягивается к одноименно заряженной проводящей сфере. Таким

образом, положение равновесия заряда a = a0	является неустойчивым.
В частном случае, когда заряды q	и Q одинаковы, корень

уравнения ξ 3

2 − ξ 2

= 1 совпадает с соответствующим корнем уравнения

(1 − ξ 2 )2

(ξ 2 + ξ − 1)(ξ 3 − ξ − 1)= 0 .

Откуда

ξ

= (

− 1)/ 2

и

0

5

a

=

R

= R(1 + ξ

) ≈ 1,618R .

0

0

ξ 0

§4. Уравнения электростатики

69

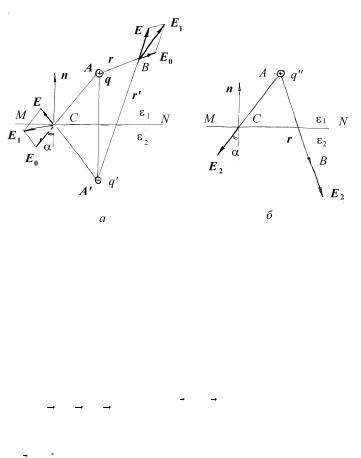
Пример 4.5. Два однородных диэлектрика с диэлектрическими проницаемостями ε1 и ε 2 граничат друг с другом вдоль плоскости. В

некоторой точке первого диэлектрика помещен заряд q . Найдите электрическое поле в каждом из диэлектриков.

Рис.4.3

Решение. Поле в среде с ε1 определяется зарядом q и связанными

зарядами, возникающими на границе диэлектриков. Покажем, что поле связанных зарядов в первом диэлектрике эквивалентно полю точечного

заряда q' ,	помещенного в		точку				A' , симметричную A относительно
плоскости	раздела диэлектриков MN . Представим полное поле как
суперпозицию полей, создаваемых зарядами q и q' (см. рис.4.3а)
		1
E1	= E 0 + E ' =		qr			+	q' r'			,
					3		r '	3
		4πε 0ε1 r
где r и r '	- векторы, проведенные от зарядов q и q' в произвольную точку
В первого диэлектрика.

69

70	§4. Уравнения электростатики
Поле в среде с ε 2	создают заряд q и связанные заряды на границе

раздела диэлектриков. Заменим последние зарядом, помещенным в точку А.

Тогда поле во втором диэлектрике будет полем точечного заряда q' ' ,

помещенного в точку А (рис.4.3б):

E 2 =	1		q' ' r	.
	4πε 0 ε 2		r 3

Для определения величин зарядов q' и q' ' воспользуемся граничными

условиями (4.6) для произвольной точки С на границе двух диэлектриков:

E

= E

,

или

q

sin α +

q'

sin α =

q' '

sin α ,

1

τ

τ 2

ε1

ε1

ε 2

Dn1 = Dn2 ,

или

q cos α − q' cos α = q' ' cosα .

Решая полученную систему уравнений, находим

q' =

ε1 − ε 2

q,

q' ' =

2ε 2

q .

ε1 + ε 2

ε1 + ε 2

Видим, что угол α

не входит в выражение для зарядов q' и q' ' , что

означает выполнение граничных условий в каждой точке плоскости MN .

Подставив q'

и

q' '

в выражения для полей, окончательно получим

E =

q

r

−

ε 2 − ε1

r '

,

E

=

1

q

r .

2

1

4πε

ε

3

ε

+ ε

2 r'

3

2πε

(ε

+ ε

)

r

3

0

1

0

1

2

1 r