electrodynamics

§1.Электрическое поле

11

равны E A

=

1

q

и E B =

1

q

откуда окончательно

,

(x + a)2

4πε 0

4πε

0

(x − a)2

напряженность в точке N равна

E

(N ) =

q

(x 2 + a 2 )

x

,

если

x

> a ,

(1.7)

x

2πε 0

(

2

− a

2 )2

x

x

E

(N ) = −

q

xa

,

если

x

< a .

x

πε 0

(

2

− a

2 )2

x

При x >> a поле

E

≈

1

2q

, то есть совпадает с полем заряда

x

4πε 0

x 2

2q .

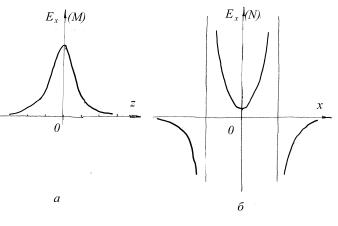
Пример 1.3. Как изменится поле в точках M и N примера 2, если заряд в точке B заменить равным, но противоположным по знаку зарядом?

Решение. При изменении знака заряда

вточке В направление вектора

напряженности E B изменится на

противоположное (рис.1.6). В этом случае поле в точке M направлено вдоль оси 0x и равно

	E x	(M ) = 2E A sin α =	1			q				a
			2πε 0			2 + z	2
					a					a 2 + z 2

Рис.1.6

qa

=2πε 0 (a 2 + z 2 )3 2 .

12	§1.Электрическое поле

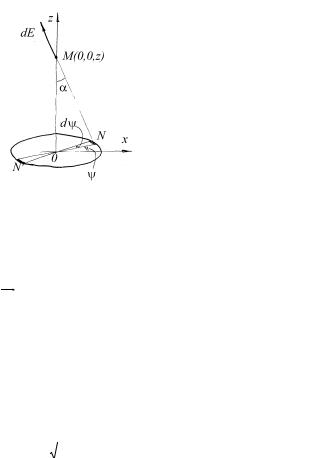
Рис.1.7

На

рис.1.7а

показана

зависимость

E x (z ) . При

z >> a поле

E

≈

1

2qa

,

то

есть

совпадает с

полем

точечного диполя

(2.8), с

x

4πε 0

z 3

дипольным моментом

p

= 2qa , которое спадает с расстоянием как

1

.

e

r 3

В точке

N (x,0,0)

напряженность поля также направлена вдоль оси

0x и равна

(N ) = −

1

q

+

q

= −

q

ax

> a ,

E x

,

если

x

(

2 )2

4πε 0

(x − a)2

(x + a)2

πε 0

2

− a

x

(N ) =

1

q

+

q

=

q

(x 2 + a 2 )

< a .

E x

,

если

x

(

2 )2

4πε

0 (x − a)2

(x + a)2

2πε

0

2

− a

x

Зависимость

E x (N ) от координаты

x иллюстрирует рис.1.7б. При

x >> a поле

E

(N ) ≈ −

1

qa

, что также совпадает с полем диполя с тем

x

πε 0 x 3

же дипольным моментом .

§1.Электрическое поле	13
Пример 1.4. Заряд Q равномерно распределен по кольцу с радиусом	a .

Найдите напряженность электрического поля в произвольной точке на

перпендикуляре

к

плоскости

кольца,

восстановленном из его центра.

Решение.

Совместим

плоскость

x0 y с

плоскостью кольца, а ось

0z −

с

его

осью

симметрии. Выберем на кольце произвольную

точку N (см. рис.1.8), определяемую

углом ψ ,

отсчитываемым от оси 0x в плоскости кольца.

Дадим

углу

ψ

малое

приращение

dψ .

Полученный

отрезок

кольца

несет

заряд

dq =

Q

dψ .

Заряд

dq

создает

в

точке

2π

(

)

напряженность

Рис.1.8

M 0,0, z

dE =

1

dq

=

1

Qdψ

.

4πε

0

a 2 + z 2

8π 2ε 0

a

2 + z 2

(1.8)

Вектор

dE

направлен вдоль отрезка NM и его проекции на оси

0x, 0 y, 0z будут равны

dE

= dE sin α cos(π + ψ ) = −

1

Qa cosψdψ

,

x

8π 2ε 0 (a 2 + z 2 )3 / 2

dE

= dE sin α sin(π

+ ψ ) = −

1

Qa cosψdψ

(1.9)

y

8π 2ε 0 (a 2 + z 2 )3 / 2

dE z

= dE cosα =

zdE

=

1

Qzdψ

.

8π 2ε

a 2 + z 2

0

(a 2 + z 2 )3 / 2

Интегрируя выражения (1.9) по ψ от 0 до 2π , находим проекции

поля, создаваемого в точке M зарядом q , распределенным по всему кольцу:

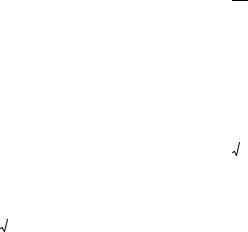
14

§1.Электрическое поле

1

Qz

2π

1

Qz

=

dψ =

E z

,

8π 2ε

0

(

2

+ z

2 )3 / 2 ∫

4πε 0

( 2

+ z

2 )3 / 2

a

0

a

1

Qa

2π

E y

= −

∫sinψdψ = 0 ,

(1.10)

8π

2

ε

(a 2

3 / 2

0

+ z 2 )

0

1

Qa

2π

E x

= −

∫cosψdψ = 0 .

8π

2

ε

(a 2

3 / 2

0

+ z 2 )

0

При решении задачи можно было бы воспользоваться симметрией

распределения заряда. Для этого выберем на кольце две точки N и N '

на

противоположных концах

диаметра. Точка

N характеризуется углом

ψ ,

отсчитываемым от оси 0x . Дадим углу ψ малое приращение dψ . Получим

два одинаковых заряда dq . Поле, создаваемое ими, было найдено в примере 2, оно направлено по оси 0z и его модуль задается выражением

Q

(1.6), в котором заряд q следует заменить на dq = 2π dψ . Интегрируя далее по углу ψ от 0 до π , находим поле, создаваемое всеми зарядами на

кольце, то есть опять приходим к выражению для E z

(1.10).

Поле

в

центре кольца

(z = 0)

равно нулю.

При

z >> a

поле

совпадает

с

полем

точечного

заряда

Q и

равно

E

≈

1

Q

.

Поле

z

4πε 0

z 2

принимает

максимальное значение при

z = z max =

a

определяемым

,

2

условием

dE z

= 0 . Максимальное значение напряженности поля при этом

dz

E

(z

) =

1

Q

.

z

max

6

3πε

a 2

0

r,θ ,ϕ ,

§1.Электрическое поле	15
Пример 1.5. На сфере радиусом a	равномерно распределен заряд Q .

Найдите напряженность электрического поля в произвольной точке пространства M .

Решение. Проведем ось 0 z из центра сферы через выбранную точку М (см.

рис.1.9). Разобьем сферу на кольца. В

сферической системе координат кольцо на сфере задается углом θ , а его

ширина -		приращением угла dθ . На нем
находится				заряд	Рис.1.9
dq =	Q	2πa sin θ adθ =	Q	sin θdθ .
4πa 2		2

Расчет поля проведем для трех случаев:

1) поле вне сферы z > a .

Согласно (1.10) поле, создаваемое в точке М этим зарядом, равно

dE z =

1

Q sin θ (z − a cosθ )dθ

.

8πε

0

([z − a cosθ ]2 + a 2 sin 2 θ )3 / 2

Поле от всей сферы получим, проинтегрировав по углу

θ

от 0 до

π . Применяя замену переменной t = cosθ , находим

E

=

Q

+1

(z − at )dt

=

Q

1

[(2z 2 − 2azt + a 2 )− a 2 ]dt

=

Q

[I (1)+ (z 2 − a 2 )I (3)]

z

8πε 0

−∫1 (a 2 + z 2 − 2azt )3 / 2

16πε 0 z −∫1

(a 2 + z 2 − 2azt )3 / 2

16πε 0 z

(1.11а)

1

dt

1

[

2−n ].

где

I (n) = ∫

=

a − z

2−n

−

a + z

(a

2 + z

2 −

n / 2

az(n − 2)

−1

2azt )

Откуда окончательно

E z =

Q

(a + z ) − (z − a) + (z

2 − a 2 )

1

−

1

=

Q

.

16πε

az 2

0

z − a z + a

4πε

0

z 2

Здесь учтено, что z > a .

16	§1.Электрическое поле

Иными словами, поле вне сферы совпадает с полем, создаваемым точечным зарядом Q , помещенным в центр сферы.

2) поле внутри сферы z < a .

Для поля внутри сферы согласно (1.11а) :

E

=

kQ

+1

(at − z )dt

=

kQ

{− I (1)+ (a 2 − z 2 )I (3)}.

(1.11б)

z

2 −∫1 (a

2 + z 2 − 2azt )3 / 2

4z

Изменятся также значения интеграла I (n) ,причем

2

2

I (1) =

,

I (3) =

( 2

− z

2 )

.

a

a a

Подставляя эти значения в (1.11б), получаем E z = 0 . Видим, что

поле внутри сферы отсутствует.

3) поле на поверхности сферы z = a .

Подставляя в (1.11а)

z = a , находим

Q

1

dt

Q

=

=

(1.11в)

E z

.

2a 2 −∫1 (1 − t )1/ 2

16πε 0

8πε 0 a 2

Поле на поверхности сферы вдвое меньше поля в точках,

находящихся вне сферы вблизи ее поверхности.

Разрывный характер поля в точках заряженной поверхности связан с пренебрежением ее реальной толщиной. Если рассмотреть заряженный сферический слой малой, но конечной толщины, то напряженность электрического поля внутри слоя будет непрерывно изменяться от нуля до максимального значения. Величина (1.11в) при этом соответствует среднему

значению напряженности внутри слоя.

Пример 1.6. Шар радиусом R равномерно заряжен по объему с объемной

	ρ =	dq
плотностью заряда ρ			. Найдите напряженность электрического
		dV

поля в произвольной точке M вне и внутри шара.

§1.Электрическое поле

17

Решение. При решении воспользуемся результатом, полученным в предыдущем примере и принципом суперпозиции. Разобьем шар на сферы.

Произвольная сфера имеет радиус r и толщину		dr , при этом на ней
равномерно распределен заряд dq = ρ 4πr 2 dr . Для		r > R			поле от каждой
сферы, как было показано в примере 5, равно dE =		dq			и направлено по
	4πε		0	r 2

радиусу от центра сферы. Поле всего шара будет равно сумме полей отдельных сфер. Так как напряженности от различных сфер в каждой точке направлены по одной прямой, то векторная сумма сведется к алгебраической и будет равна

4

π R 3 ρ

Q

=

=

ρ R 3

.

E =

3

(1.12)

4πε 0 r 2

4πε 0 r 2

3ε 0 r 2

Здесь Q - заряд всего шара.

Для

r < R

вклад в поле будут давать только заряды на сферах,

радиус которых не превышает r , или

4

π r 3 ρ

E =

Q'

=

3

=

ρ r

.

(1.13)

4πε 0 r 2

4πε 0 r 2

3ε 0

Здесь заряд Q' заключен внутри шара радиусом

r . В этом случае

Е −непрерывная на границе шара функция.

Пример 1.7. Тонкая палочка длины l заряжена равномерно с линейной плотностью κ . Найдите напряженность электрического поля, создаваемого зарядом на палочке, в произвольной точке пространства М.

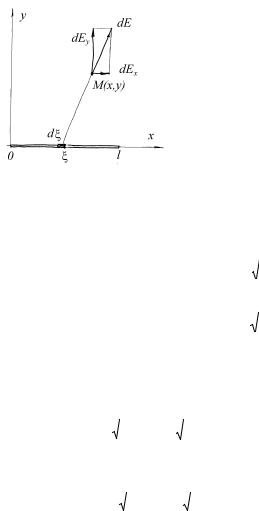
18			§1.Электрическое поле
	Решение. Совместим начало координат с
	одним	из	концов палочки, ось 0x
	направим вдоль палочки, а ось 0 y
	направим		так, чтобы плоскость			z = 0
	содержала		точку M (x, y), в		которой
	вычисляется поле (рис.1.10). Таким
	образом, используя симметрию поля
	относительно оси 0x , сведем				задачу к
	двумерной. Выделим на палочке малый
Рис.1.10	элемент	dξ на расстоянии		ξ	от	начала
	координат.		Вклад элемента	с	зарядом

dq = κdξ в поле согласно закону Кулона равен

dE x

= dE cosα =

1

κdξ

(x − ξ )

,

(1.14)

4πε

(x − ξ )2 + y 2

0

(x − ξ )2 + y 2

dE y

= dE sin α =

1

κdξ

y

.

(1.15)

4πε

(x − ξ )2 + y 2

0

(x − ξ )2 + y 2

Поле от всего заряда, распределенного по палочке, получим,

проинтегрировав (1.14) и (1.15) по ξ от 0 до l :

κ

1

1

E x

=

−

(1.16)

4πε 0

2

+ y

2

2

+ y

2

x

(x − l )

и

κ

x

x − l

E

=

−

.

(1.17)

y

4πε 0 y

2

+ y

2

(x − l )

2

+ y

2

x

Заметим, что последние формулы можно представить в виде:

E x	=	κ		(sin ϕ	2 − sin ϕ1 )	(1.16а)
		4π ε
			0 a

	§1.Электрическое поле								19
	E y =	κ		(cosϕ1		− cosϕ 2 )			(1.17а)
		4π ε
			0 a
	В этих формулах углы ϕ1 и ϕ2 образованы положительным
	направлением оси 0x				и прямыми, соединяющими концы палочки с точкой
	М.
	Отметим, что выражение (1.17) для E y при y → 0								(x > l ) приводит
	к неопределенности				типа		0	. При малых y формулу	(1.17) следует
						0

преобразовать, например, взяв лишь первый отличный от нуля член разложения E y в ряд Тейлора около значения y = 0 :

	≈	κy		1	−	1
E y								.	(1.18)
		8πε 0		(x − l )2			2
						x

Бесконечности, возникающие в выражениях (1.16)-(1.18) на концах палочки, связаны с тем, что при расчете полей толщина палочки считалась равной нулю. Поэтому поле в непосредственной близости от поверхности палочки на самом деле будет отличаться от поля, задаваемого выражениями

(1.16)-(1.18). Тот факт, что напряженность поля минимальна в середине палочки и растет к ее концам, связан с тем, что для точек, лежащих на равном расстоянии от концов палочки, вклад в поле зарядов, находящихся симметрично на разных половинах палочки, максимально компенсируется при сложении полей.

Аналогичная компенсация имеет место и для палочки конечной толщины. Поэтому поле равномерно заряженной палочки максимально вблизи ее концов.

Пример 1.8.Тонкая палочка длины l заряжена так, что линейная плотность заряда κ линейно зависит от расстояния до центра палочки. Полный заряд палочки равен нулю. Половина палочки несет заряд q . Вычислите

дипольный момент палочки pe .

20 §1.Электрическое поле

Решение. Направим ось 0x вдоль палочки, совместив при этом ее начало с серединой палочки. Выделим на палочке два маленьких кусочка длиной dx

с координатами x и - x . На них располагаются равные по величине и различные по знаку заряды dq и - dq , причем dq = κdx . По условию задачи

κ = αx . Значение постоянной α выразим через заряд половины палочки q

l / 2

q = ∫ κdx = αl 2

,

или

α =

8q

.

2

0

8

l

Заряды

dq и

- dq

образуют

диполь

с дипольным моментом

dp

= 2xdq =

16q

x 2 dx .

Полный дипольный

момент палочки найдем,

e

l

2

просуммировав дипольный момент по всей палочке

16q

l / 2

2ql

p

=

∫

x 2 dx =

.

e

l

2

3

0

Направлен дипольный момент вдоль палочки, от отрицательно заряженного конца к положительному.

Задание для самостоятельной работы
1.1. Три одинаковых точечных заряда	q	расположены в		вершинах
равностороннего треугольника, а точечный		заряд q'	--	в центре
треугольника. Каким должен быть заряд	q' ,	чтобы сила, действующая на
каждый заряд, была равна нулю?

1.2.Найдите модуль и направление напряженности поля E в центре кольца радиуса a , в котором сделана прорезь ширины b << a . По кольцу равномерно распределен заряд q > 0 .

1.3.Найдите отношение силы электростатического отталкивания двух электронов к силе их гравитационного притяжения. Масса электрона