Математика производные и пределы

ПРИМЕР. Вычислите односторонние пределы функции y = xx ++ 33 .

По определению модуля

x +3		x +3,	x ≥ −3,
	=
	−x −3,		x < −3,

lim		x +3	=	lim	x +3			= lim (−1) = −1,
		x +3			−(x +3)
x→−3−0				x→−3−0				x→−3−0
lim		x +3	=	lim	x +3	=		lim 1 =1.
		x +3			(x +3)
x→−3+0				x→−3+0				x→−3+0

3.4. Бесконечно малые функции и их свойства

Функция α (x) называется бесконечно малой в точке a , если limα (x)= 0 .

x→a

Аналогично определяется функция, бесконечно малая при x → +∞

( x → −∞).

Свойства бесконечно малых функций:
1. Если limα (x)= lim β (x)= 0 , то lim			(	α (x)+ β (x)	)	= 0 .
x→a	x→a	x→a

Свойство может быть расширено: сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть функция бесконечно малая.

			2	sin	1	= 0, т.к. x	2	- бесконечно малая функция в точке
Например, lim x
	1	x→0			x
x = 0 , а sin		- ограниченная функция.
	x

3. Произведение бесконечно малых функций есть функция бесконечно малая.

3.5. Сравнение бесконечно малых функций

Пусть функции α1 (x) и α2 (x) являются бесконечно малыми при x → x0 .

Если lim α1 (x) = A, то возможно несколько ситуаций:

x→x0 α2 (x)

1) если A < ∞ и A ≠ 0 , то α1 (x) и α2 (x) называются бесконечно малыми одного порядка;

31

2) если A =1, то α1 (x) и α2 (x) называются эквивалентными. Обозначе-

ние: α1 (x) α2 (x) ;

3)если A = 0 , то функция α1 (x) называется бесконечно малой высшего порядка по сравнению с α2 (x). Обозначение: α1 (x) = o (α2 (x)) .

4)если α (x) α1 (x) и β (x) β1 (x) являются эквивалентными бесконеч-

но-малыми при x → x , то lim

α (x)

= lim

α1

(x)

.

β1

0

x→x0

β (x)

x→x0

(x)

Доказательство: lim

α (x)

= lim

α (x)α1 (x)β1

(x)

=

β (x)

β (x)α1 (x)β1 (x)

x→x0

x→x0

α (x)

β1

(x)

α1

(x)

α (x)

β1

(x)

α1

(x)

α1

(x)

= lim

=

= lim

lim

lim

= lim

.

α1 (x)

β

(x)

β1

(x)

α1 (x)

β

β1

(x)

β1

x→x0

x→x0

x→x0

(x)

x→x0

x→x0

(x)

Аналогично: если α1 (x) α2 (x) при x → x0 , то

1). lim ( f (x) α1

(x))= lim ( f (x) α2 (x));

x→x0

x→x0

2). lim

α1 (x)

= lim

α2 (x)

;

x→x0

f (x)

x

→x0

f (x)

3).

lim f (α1 (x))= lim f (α2 (x)).

x→x0

x→x0

ПРИМЕР. Функции α1 (x)= х2

и α2 (x)= 2х2 + х3

являются бесконечно малыми

одного порядка малости при х→ 0

так как

lim

х2

= lim

х2

= lim

1

=

1

.

2x2 + х3

x2 (2 + х)

2

+

х

2

x→0

x→0

x→0

В то же время функции α1 (x)= х2

и α2 (x)= 2х2 + х

не являются бесконечно

малыми одного порядка при x → 0 , так как

lim

х2

= lim

х2

= lim

х

= 0.

2х2 + х

x(2х+1)

x→0

x→0

x→0 2х+1

Таким образом,

α1 (x)= х2

имеет более высокий порядок малости при х→ 0

чем α2 (x)= 2х2 + х.

ПРИМЕР. Функция α1 (x)= е−х

является бесконечно малой более высокого по-

рядка малости при х→ +∞ чем

α2 (x)= 2−х

. Действительно,

lim

е−х

= lim

е−х

= lim е−х+ln 2 x

= lim

ех(ln 2−1)

= 0.

2−х

x→+∞

x→+∞ е−ln 2 х

x→+∞

x→+∞

32

3.6. Бесконечно большие функции и их свойства

	Функция	f (x) называется бесконечно большой в точке a , если
	lim f (x) = + ∞ M δ (M ) > 0 x (0 <			x − a		<δ		f (x)		> M ).
	x →a
		определяются функции, бесконечно большие при x → +∞
	Аналогично
	(x → −∞).

Функция, бесконечно большая при x → a , является неограниченной в окрестности точки a , но обратное утверждение неверно: не всякая неограниченная функция является бесконечно большой.

Функция f1 (x)= 1x является бесконечно большой при x → 0 , так как для

любого числа M можно указать окрестность точки x = 0 , в каждой точке которой f (x) < M .

		1
	sin
Функция f2 (x)=	x		является неограниченной при	x → 0 , но беско-
	x
нечно большой не является. Для этой функции для любого числа M в каждой
окрестности точки x = 0		можно указать точку, в которой				f (x)		> M , но в

этой же окрестности найдутся точки, не удовлетворяющие этому условию, для которых, например, f (x)= 0 .

Свойства бесконечно больших функций:

1.Произведение функции, бесконечно большой в точке a , на ограниченную и отличную от нуля функцию есть функция бесконечно большая в точке а.

2.	Произведение функций, бесконечно больших в точке a , есть функция
	бесконечно большая в точке а.
3.	Сумма функций, бесконечно больших в точке a , может не быть беско-
	нечно большой функцией.

ПРИМЕР. Пусть f (x), g (x) - бесконечно большие при x → ∞.

1). Если f (x)= x , g (x)=1− x2 , то f (x)+ g (x)=1+ x − x2 является бесконечно большой функцией.

33

2). Если f (x)= x , g (x)=1− x , то f (x)+ g (x)=1 не является бесконечно большой функцией.

3.7. Связь между бесконечно большими и бесконечно малыми функциями

Если α (x) - бесконечно малая функция при x → a и α (x) ≠ 0 при x ≠ a ,

то α (1x) - бесконечно большая функция при x → a . Если α (x) - бесконечно

большая при x → a , то α (1x) - бесконечно малая.

3.8. Свойства функций, имеющих предел

Теоремы этого раздела сформулированы для пределов в точке x0 , но все они справедливы и для пределов при x → ±∞.

Теорема 1
Если lim f (x) = A, A <∞, то f (x)= A +α (x), где lim α (x)= 0 .
x→x0					x→x0
Доказательство:
Если lim f (x) = A,	то, по определению Коши, при произвольном ε > 0 вы-
x→x0			f (x)− A				f (x)− A		=α (x). Тогда для
полняется неравенство					< ε . Обозначим

любого ε > 0 выполняется α (x) < ε . Но это и означает, что α (x) – бесконечно

малая при x → x0 .

Справедливо и обратное утверждение: если функция f (x) представима в

виде f (x)

= A +α (x), где lim α (x)= 0 , то существует lim f (x) = A.

Теорема 2

x→x0

x→x0

и y =ϕ(x) определены в окрестности точки x0 D .

Пусть функции y = f (x)

Если lim f (x)= A и lim ϕ(x) = B , то

x→x0

x→x0

1) lim

(

f (x)+ϕ (x)

)

= lim f

(x)+ lim ϕ (x),

x→x

x→x

x→x

0

(

)

0

0

2) lim

f (x) ϕ (x)

= lim f (x) lim ϕ (x),

x→x

x→x

x→x

0

(

(

))

0

(

)

0

x→x

k f

x

x→x

x

,

3) lim

= k lim f

0

0

34

	4) lim	f (x)	=	xlim→x	f (x)	, где
				0
		ϕ(x)		lim ϕ(x)
	x→x0
				x→x0

lim ϕ(x)≠ 0 .

x→x0

Доказательство первого утверждения теоремы 1.

Из теоремы о связи функции, предела и бесконечно малой следует, что

f (x)+ϕ(x)= (A+α(x))+(B + β (x))= (A+ B)+(α(x)+ β (x))= A+ B +γ (x).

Так как γ (x)

=α (x)

+ β (x), lim γ(x) = lim (α(x) + β(x))= 0 ,

получаем

x→x0

x→x0

lim ( f (x) +ϕ(x))= A + B = lim

f (x) + lim ϕ(x) .

x→x0

x→x0

x→x0

ПРИМЕР. Вычислите предел lim

x2

+5

.

x2

−3

x2 +5

x→2

Функция

f (x) =

определена в точке x = 2 , поэтому

x2 −3

0

lim

x2

+5

= f

(2) =

22

+5

=

9 .

x2

−3

22

−3

x→2

ПРИМЕР. Вычислите предел lim

x3 + x

.

−3x2 +1

x→∞ x3

От бесконечно больших значений аргумента перейдем к бесконечно малым. Для этого, как и для последовательностей, применим метод деления числителя

и знаменателя на наивысшую степень x , т.е. на x3 :

lim

x3 + x

∞

= lim

1+1 x2

1 + 0

=1.

=

=

3

−3x

2

+1

1

−3 x +1 x

3

1

−

0 + 0

x→∞ x

∞

x→∞

	ПРИМЕР. Вычислите предел lim	9 +5x + 4x2 −3	.
		x
	x→0

Непосредственно подставляя число x0 = 0 в функцию, получаем неопределен-

ность	0		. Учтем формулу	(a −b)(a	+b)= a	2	−b	2	и умножим числитель и зна-
	0				+3):
менатель на выражение ( 9 +5x + 4x2

35

lim	9 +5x + 4x2 −3		0		= lim	(	9 +5x + 4x2 )2 −(3)2
			=					9 +5x + 4x2 +3)	=
x→0	x		0		x→0 x (

= lim

9 +

5x + 4x2

−9

= lim

5 + 4x

=

5 +0

=

5

=

5

.

x→0 x ( 9 +5x + 4x2 +3)

x→0 9

+5x + 4x2

+3

9

+0 +0

+3

3

+3

6

3.9. Предельный переход в неравенствах

Теорема о сохранении знака неравенства при предельном переходе.

Если функции y = f (x) и y =ϕ(x) в окрестности точки x0 D удовлетворя-
ют	неравенству	f (x)≤ϕ(x)	и	имеют конечные пределы, то
lim	f (x) ≤ lim ϕ(x).
x→x0	x→x0
Теорема о пределе промежуточной функции.
Если для функций		f (x),ϕ(x), g (x) в окрестности точки x0 D выполняет-
ся неравенство f (x)		≤ϕ(x)≤ g (x)	и lim f (x) = lim g(x) = A, то функция ϕ(x)
			x→x0	x→x0

имеет тот же предел lim ϕ(x) = A .

x→x0

4.НЕПРЕРЫВНОСТЬ ФУНКЦИИ

4.1.Непрерывность функции в точке

Пусть функция y = f (x) определена в окрестности точки x0 D . Определение 1. Функция y = f (x) называется непрерывной в точке x0 ,

если функция определена в точке x0 , существует предел	lim f (x) и при этом
lim f (x) = f (x0 ) .	x→x0
x→x0
При нарушении любого из трех условий: 1) f (x0 ) , 2) lim	f (x) ,
x→x0

3) lim f (x) = f (x0 ) ) функция называется разрывной в точке x0 .

x→x0

ПРИМЕР

x2 , x < 0,

Функция f (x) = непрерывна в любой точкеx0 ≠ 0

1, x ≥ 0

и разрывна в точке 0 (нарушено второе условие определения).

36

Определение 2

Рассмотрим точку x0 D функции y = f (x) и точку x ≠ x0 .

Величина ∆x = x − x0 называется приращением аргумента, x = x0 +∆x .

Величина ∆ y = f (x0 + ∆x)− f (x0 ) называется приращением функции, соответствующим данному приращению аргумента ∆x .

Функция y = f (x) называется непрерывной в точке x0 , если функция опреде-

лена в точке x0 и при этом lim ∆y = 0.

∆x→0

Итак, функция непрерывна в точке, если бесконечно малым приращениям аргумента соответствуют бесконечно малые приращения функции.

ПРИМЕРЫ

1. Функция y = x2			непрерывна в произвольной точке x вещественной оси.
∆y = (x + ∆x)								0
		2 − x	2 = x 2 + 2x ∆x +∆x2 − x 2 = 2x ∆x +∆x2.
0		0	0	0	0		0
lim ∆y = lim (		2x0 ∆x +∆x2 )= 2x0 lim ∆x + lim ∆x lim ∆x = 2x0 0 + 0 0 = 0.
∆x→0	∆x→0			∆x→0	∆x→0		∆x→0
2. Функция		y =sin x непрерывна в произвольной точке x0								вещественной оси.
Если х > 0 , то из неравенства 0 < sin x < x следует, что
0 ≤ lim sin x ≤ lim x = 0, т.е.				lim sin x =0. Если х< 0 , то					х < sin x < 0 и анало-
x→0+0		x→0+0		x→0+0			limsin x =0.
гично получаем lim sin x = 0 . Таким образом
		x→0−0					x→0
Используя второе определение непрерывности, в произвольной точке x0
имеем	lim	(sin (x0 + ∆x)−sin x0 )= lim					∆x		+	∆x
					2sin		cos x0				= 0 ,
	∆x→0			∆x→0			2			2

так как lim sin ∆х =0, а косинус является ограниченной функцией. Непрерыв-

∆x→0 2

ность синуса доказана.

3. Функция y = соs x непрерывна в произвольной точке x0 вещественной оси.

∆y = соs(x0 + ∆x) - соs x0 = -2 sin (∆x/2) sin (x0 + ∆x/2),

lim ∆y = −2 lim sin		∆x			+	∆x	= 0 ,
		2	lim sin x0
∆x→0	∆x→0		∆x→0			2

как произведение бесконечно малой функции на ограниченную функцию.

37

Так как lim x = x0 , то для непрерывной функции
x→x0		)
lim f (x) = f (x0 )= f	lim(x)		, то есть символы функции и предела перестано-
x→x0	(x→x0

вочны.

Определение 3

Функция y = f (x) называется непрерывной в точке x0 , если

1)	функция определена в точке x0 ,
2)	существуют односторонние пределы lim f (x),			lim f (x) ,
		x→x0	−0	x→x0 +0
3)	lim	f (x) = lim f (x) = f (x0 ) .
	x→x0 −0	x→x0 +0

Все три определения непрерывности равносильны.

Покажем, что 2-е определение непрерывности равносильно 1-му определению.

Используя арифметические свойства предела, получаем
lim ∆y =	0,	lim [f (x0 + ∆x) − f (x0 )]		= 0,
∆x→0		∆x→0
lim f (x0	+ ∆x) − lim f (x0 ) = 0,		lim	f (x0 + ∆x) − f (x0 ) = 0.
∆x→0		∆x→0	∆x→0
По определению приращения ∆x = x – x0, поэтому lim f (x0					+ ∆x) = lim f (x),
				∆x→0	x→х0
и тем самым lim f (x) − f (x0 ) = 0, или			lim f (x) = f (x0 ) .
x→х0			x→х0

Последнее равенство и означает 1-е определение непрерывности.

Используется также понятие односторонней непрерывности.

Функция y = f (x) называется непрерывной в точке x0 слева, если функция

определена в точке x0 и существует односторонний предел lim f (x) и при

x→x0 −0

этом lim	f (x) = f (x0 ) .
x→x0 −0
Функция	y = f (x) называется непрерывной в точке x0 справа, если функ-
ция определена в точке x0			и существует односторонний предел lim f (x) и
			x→x0 +0
при этом x→limx +0		f (x) = f (x0 ) .
	0

Используя понятие односторонней непрерывности, можно сказать, что функ-

ция непрерывна в точке x0 , если она непрерывна в ней справа и слева.

38

4.2. Непрерывность функций на множестве

Функция, непрерывная в любой точке множества D ,

называется непре-

рывной на множестве D .

Функция непрерывна на отрезке [a,b], если она непрерывна на интервале

(a,b), непрерывна справа в точке a и непрерывна слева в точке b .

4.3. Свойства функций, непрерывных в точке

Если функции

y = f (x) и

y =ϕ (x) определены на множестве D и непре-

рывны в точке x0 D , то функции

f (x)

f (x)+ϕ (x), k f (x)

(k = const ),

f (x) ϕ (x),

ϕ (x)

непрерывны в точкеx0 , причем частное требует условия ϕ (x0 )≠ 0 .

В частности:

1). Многочлен P (x)= a xn + a

n−1

xn−1 +... + a x + a

непрерывен в любой точке x

n

n

1

0

0

вещественной оси.

P (x)

a xn +... + a x + a

2). Дробно-рациональная функция

R(x) =

=

непрерыв-

n

n

1

0

Q (x)

b xm +... +b x +b

m

m

1

0

на в любой точке x0 вещественной оси, где Qm (x0 )≠ 0 .

Если функция y = f (x) непрерывна в точке x0 , то она ограничена в некоторой окрестности этой точки.

4.4. Непрерывность основных элементарных функций

Основными элементарными функциями обычно называют следующие функции:

y = xα , ax , loga x , sin x , cos x , tg x , ctg x , arcsin x , arccos x , arctg x , arcctg x .

Основные элементарные функции непрерывны в каждой точке x0 их области определения.

Непрерывность функций			sin x и cos x была установлена выше в п.4.1. Из
свойств непрерывных функций			следует, что функция tg x непрерывна всюду
кроме	точек	x = π +πn, n Z , а функция ctg x всюду кроме точек
x =πn,	n Z .	2

39

5.ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Втеории пределов большую роль играют два предела, которые, в силу их важности, получили названия замечательных пределов.

5.1.Первый замечательный предел

Функция y = sinx x при x → 0 имеет предел, равный 1:

lim sin x =1.

x→0 x

Доказательство:

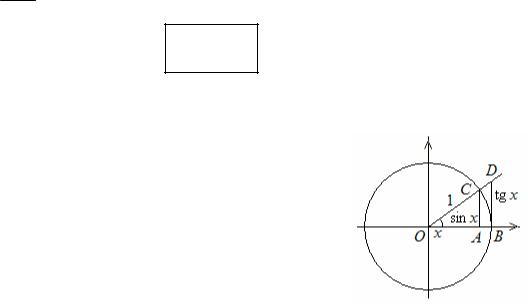
Рассмотрим единичную окружность.

Пусть

COB = x ,

0 < x <

π

,

OC = OB = r =1,

2

AC = sin x , OA = cos x ,

BD = tg x . Сравнивая площади

треугольника OAC , сектора OBC и треугольника

OBD , получаем

S OAC < SOBC < S OBD ,

sin x .

1 sin x cos x < 1 x <

1

2

2

2

cos x

x

Разделим двойное неравенство на

sin x (> 0): cos x <

<

1

. Неравенство

sin x

cos x

2

справедливо и для x < 0 , так как cos(−x) = cos x,

sin(−x)

= sin(x) . Перейдем к

−x

x

пределу при x → 0 : cos(x) - функция непрерывная,

cos x → cos(0) =1. Приме-

няя теорему о пределе промежуточной функции, получаем

1 ≤ lim sin x ≤1, то есть lim sin x

=1.

x→0

x

x→0

x

Впервом замечательном пределе имеет место неопределенность 0 .

0

ПРИМЕР. Вычислите предел: lim sin 2x .

x→0 x

Если x → 0, то и 2x → 0 и тогда

lim	sin 2x		0		= lim	2 sin 2x	= 2 lim	sin 2x	= 2	1 = 2.
	x	=				2 x		2x
x→0		0			x→0		x→0

40