MP_praktikumNG

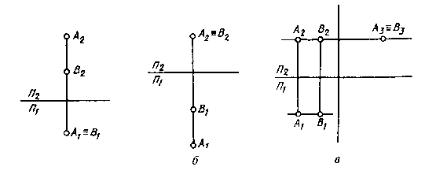
-Свойство. Положение точки в пространстве вполне определяется положением двух ее ортогональных проекций.

-Следствие. По двум любым заранее заданным проекциям точки всегда можно построить недостающую третью проекцию.

Конкурирующие точки

Две точки в пространстве могут быть расположены поразному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими.

На рис. 1.8, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости π1 [А1≡В1]. Такие точки называются горизонтальноконкурирующими. Если проекции точек A и В совпадают на плоскости π2 (рис. 1.8, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости

					в
а			б
	-

Рис. 1. 8. Конкурирующие точки: а – горизонтальноконкурирующие; б – фронтально–конкурирующие; в – профильно - конкурирующие

По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота (А), у фронтально-конкурирующих та, у которой больше глубина (А), и у профильно-конкурирующих та,

у которой больше широта (А).

10

Четверти и октанты пространства

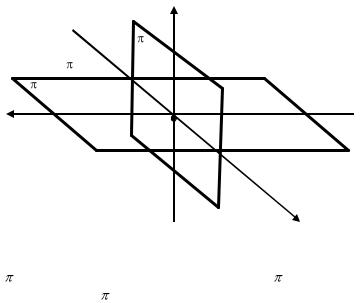
Плоскости π1 и π2 образуют в пространстве четыре двугранных угла. Их называют квадрантами или четвертями пространства. При вводе плоскости проекций π3 мы получаем восемь октантов пространства. Считается, что зритель всегда находится в первой четверти или в первом октанте пространства (рис. 1.9).

Z+

II

3

VI

2 I

V

1

VII

X+

III

О

IV

VIII

Y+

Рис. 1.9. Декартова система координат

1 – горизонтальная плоскость проекций;

2 – фронтальная

плоскость проекций;

3 – профильная плоскость проекций

Оси: X – абцисс, Y – ординат, Z – аппликат.

Точка О – начало координат.

Плоскости проекций делят пространство на 8 октантов.

При отчете координат точки и данном направлении осей

получим:

Октант

X

Y

Z

Октант

X

Y

Z

I

+

+

+

V

-

+

+

II

+

-

+

VI

-

-

+

III

+

-

-

VII

-

-

-

IV

+

+

-

VIII

-

+

-

11

1.6. Ортогональные проекции прямой

Для определения проекции прямой, достаточно знать проекции двух точек, принадлежащих этой прямой.

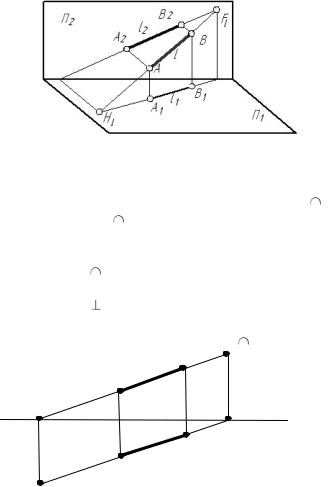
Прямая l, которая пересекает три проекционные плоскости, называется прямой общего положения (рис. 1.10).

Рис. 1.10. Прямая общего положения

Точка пересечения прямой l c плоскостью проекций, называется следом прямой. H1 - горизонтальный след H1= l π1; F1 – фронтальный след F1= l π2;

Для нахождения горизонтального следа прямой надо:

1)отметить точку пересечения фронтальной проекции

прямой l с осью x: l2 x = H2;

2)через полученную точку провести прямую a перпен-

дикулярную оси x: a x ;

3)пересечение a с горизонтальной проекцией прямой

укажет положение горизонтального следа: a l1 = H1 (рис. 1. 11).

		F2
	l2	В2
	A
	Н
	l1	F1
		В1

A

Н	Рис. 1.11. Комплексный чертеж прямой

12

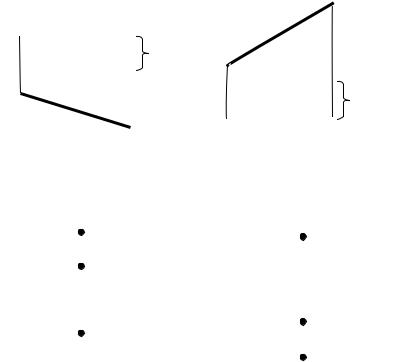
1.7. Прямые частного положения (параллельные и перпендикулярные к плоскостям проекций)

Прямые, параллельные плоскостям проекций, являются прямыми уровня и называются горизонтальной и фронтальной

(рис. 1.12, 1.13).

		h2							f2
				const
x
							x			const
		h1							f1
	Рис. 1.12. Горизонтальная прямая							Рис. 1.13. Фронтальная прямая

Прямые, перпендикулярные плоскостям проекций, называются проецирующими прямыми (рис.1.14, 1.15).

	a2	b2≡F21
x	a1≡H1	x
		b1

Рис. 1.14.	Рис. 1.15.
Горизонтально проецирующая	Фронтально проецирующая
прямая	прямая

Прямые, лежащие в плоскостях проекций, называются прямыми нулевого уровня (рис. 1.16).

13

f02

а

f0 π2

x

f01

h02

б

x

h0 π1

h01

Рис. 1.16. Прямые нулевого уровня

h0 и f0 являются нулевыми a-горизонтально и б-фронтально

1.8. Взаимное положение прямых линий

Две прямые могут пересекаться между собой, быть параллельными или скрещиваться.

Если две прямые параллельны, то на комплексном чертеже их одноименные проекции параллельны (рис. 1.17, а).

Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи

(рис. 1.17, б).

Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 1.17, в).

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 1.17, г).

14

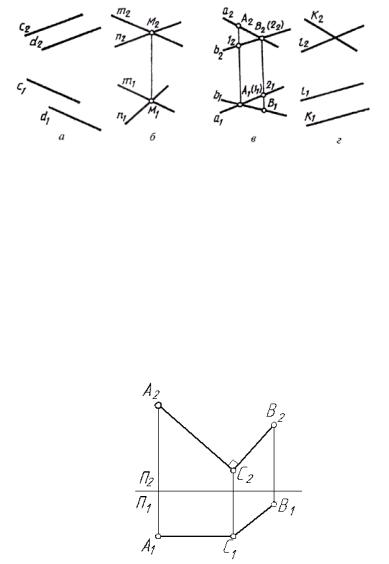
Рис. 1.17. а- параллельные прямые; б- пересекающиеся прямые; в- скрещивающиеся прямые, г- скрещивающиеся прямые

1.9.Теорема о прямом угле

1.Если плоскость, в которой расположен некоторый угол, перпендикулярна к плоскости проекций, то он проецируется на эту плоскость проекций в виде прямой линии.

2.Если плоскость прямого угла не перпендикулярна к плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла

(рис. 1.18).

Рис. 1.18. Проецирование прямого угла

15

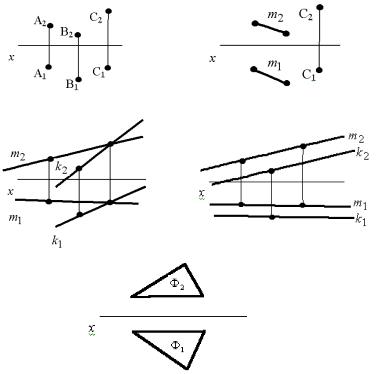
1.10. Плоскость.

Плоскость является простейшей поверхностью.

Положение плоскости в пространстве однозначно определяется тремя точками A, B и С, поэтому на эпюре Монжа достаточно указать проекции (рис. 1.19 а, б, в, г):

а

б

в

г

д

Рис. 1.19. Способы задания плоскости: а - тремя точками не принадлежащими одной прямой; б - прямой m и не принадлежащей ей точкой С; в - двумя прямыми пересекающимися в точке или двумя параллельными прямыми; г - проекциями плоскостей фигуры, принадлежащей плоскости

16

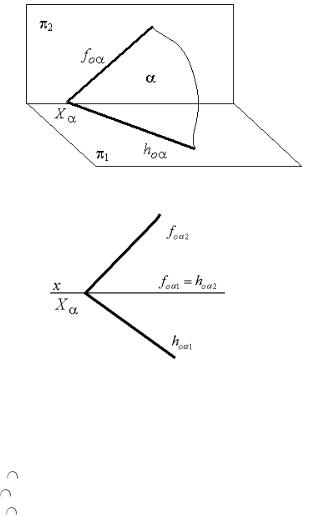
Плоскость можно задавать прямыми, по которым эта плоскость α пересекает проецирующие плоскости (рис. 1.20, 1. 21).

Рис. 1.20. Следы плоскости

Рис. 1.21. Плоскость α задана следами

Это дает более наглядное изображение положения плоскости в пространстве. Такой способ задания плоскости называется заданием плоскости следами.

При этом различают:

h0α= α π1 - горизонтальный след плоскости α; f0α=α π2 фронтальный след плоскости α;

Xα = x α точка схода следов.

17

1.11. Частные случаи расположения плоскости

Плоскости, перпендикулярные плоскостям проекций, называются проецирующими (рис. 1.22, 1.23).

Рис. 1.22.	Рис. 1.23
Горизонтально проецирующая	Фронтально проецирующая
плоскость	плоскость

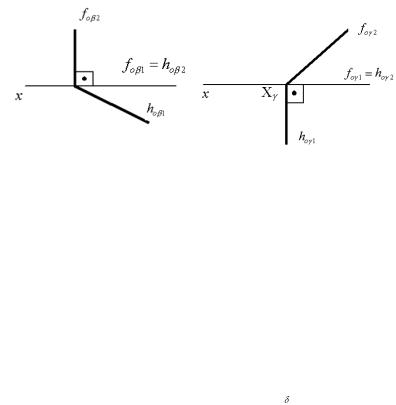
Плоскости, параллельные плоскостям проекций, называются горизонтальными и фронтальными (рис. 1.24, 1.25).

fo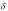

x

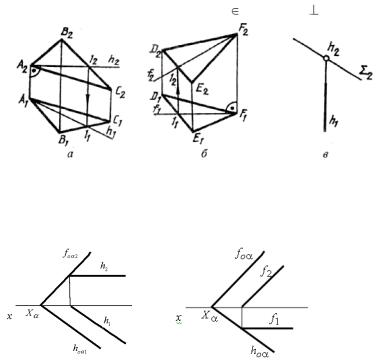
Рис. 1.24. Горизонтальная плоскость δ // π2

x	fo

Рис. 1.25. Фронтальная плоскость ε // π2

1.12.Особые линии плоскости

Кособым линиям в плоскости можно отнести линии, параллельные плоскости проекций. Их называют линиями уровня.

18

Линию, принадлежащую плоскости и параллельную горизонтальной плоскости проекций, называют горизонталью плоскости. Построение горизонтали всегда начинают с ее фронтальной проекции (рис. 1.26 а).

Линию, принадлежащую плоскости и параллельную фронтальной плоскости проекций, называют фронталью плоскости. Построение фронтали начинают с горизонтальной проекции (рис.

1.26, б).

Рассматривая особые линии в плоскостях частного положения, можно убедиться, что соответствующие линии уровня в этом случае будут проецирующими.

На рис. 1.26, в показана горизонталь h фронтально проецирующей плоскости Sum. В данном случае она будет также фронтальной проецирующей прямой, т. е. h Sum; Sum π2.

Рис. 1.26 Особые линии в плоскости треугольника: а- горизонталь, б- фронталь; в- горизонталь фронтально

проецирующей плоскости

Особые линии плоскости также могут быть заданы в плоскостях, заданных следами (рис. 1.27 а, б).

Рис 1.27. Особые линии в плоскости, заданной следами: а- горизонталь, б- фронталь

19