MP_praktikumNG

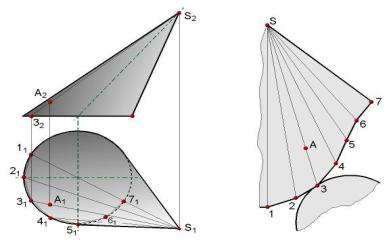
получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа.

1.20. Построение разверток кривых развертывающихся поверхностей

Построение точных разверток кривых развертывающихся поверхностей сложно и, как правило, не вызывается практической необходимостью. Поэтому обычно строят приближенные развертки поверхностей, вполне пригодные для практических целей. Основным способом построения приближенных разверток развертывающихся поверхностей (кроме цилиндрических) явля-

ется способ триангуляции поверхности. Он состоит в том, что кривая поверхность заменяется многогранной поверхностью, состоящей из треугольных граней. Рассмотрим применение способа триангуляции к построению развертки эллиптического конуса,

(рис. 1.47).

Рис. 1.47. Построение развертки эллиптического конуса

Триангуляция конической поверхности осуществляется вписыванием в нее пирамидальной поверхности, которая опреде-

40

ляется ломаной 1 - 2 - 3 - 4, ..., вписанной в направляющую кривую конуса, и вершиной S. Развертка этой n-угольной пирамиды и принимается за развертку конуса. Ломаная линия 1 - 2 - 3 - 4, ..., получающаяся на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки.

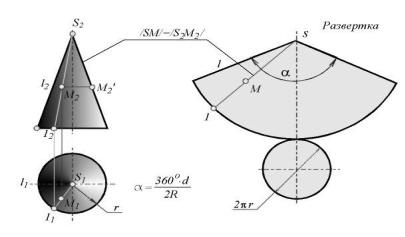
Развертка прямого кругового конуса, образующая которого равна / l / и радиус основания / r /, имеет форму кругового сектора с радиусом равным / l / и центральным углом = 360o| r | / | l | - (рис. 1.48).

Рис. 1.48. Развертка прямого кругового конуса

При построении разверток цилиндрических поверхностей способ триангуляции, как правило, не применяется.

Цилиндрическая поверхность заменяется (апроксиммируется) вписанной в нее призматической поверхностью, которая определяется ломаной 1 - 2 - 3 - 4, ..., вписанной в направляющую кривую цилиндра, и направлением образующих. Развертка этой п-угольной призмы и принимается за развертку цилиндра. Ломаная линия 1 - 2 - 3 - 4, ..., получающаяся на развертке призмы, заменяется плавной кривой, проходящей через те же точки. Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник со сторонами, соответственно равными 2пr и h, где r - радиус окружности основания цилиндра, а h - его высота (рис. 1.49).

41

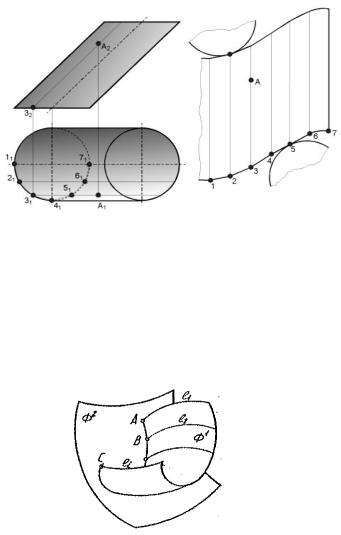
Рис. 1.49. Построение развертки цилиндрической поверхности

1.21. Взаимное пересечение поверхностей

Задачу построения линии пересечения двух поверхностей часто называют пятой позиционной задачей.

Искомая линия пересечения определяется как множество точек пересечения линий каркаса первой поверхности Ф1 со второй поверхностью Ф2 (рис. 1.50).

Рис. 1.50. Пересечение поверхностей

Последовательно перебирая образующие 1 , 2 ,... i карка-

са одной поверхности, необходимо найти точки А, В,…С, в которых эти образующие пересекаются со второй поверхностью.

42

Реализация этой методики связана с трудоемкими построениями на эпюре, которые в некоторых случаях удается избежать.

Например, в случаях пересечения поверхностей, когда линии их каркаса попарно расположены на общих плоскостях или сферах. Построение таких каркасов легко осуществить для некоторых случаев пересечения поверхностей вращения, линейчатых и циклических.

Способ вспомогательных секущих плоскостей

Этот способ рекомендуется применять в том случае, когда сечениями заданных поверхностей одной и той же плоскостью являются прямые линии и окружности. Также применяется способ вспомогательных секущих плоскостей в случае, когда одна из пересекающихся поверхностей – гранная.

Рассмотрим пример построения линии пересечения полусферы с поверхностью прямой треугольной призмы (рис. 1.51).

Рис. 1.51. Применение способа вспомогательных секущих плоскостей

43

Как видно, условие задачи удовлетворяет требованиям применения способа вспомогательных секущих плоскостей. Однако, путей решения задачи несколько.

Очень важно правильно выбрать семейство вспомогательных плоскостей, которые дают наиболее быстрое и простое решение. Для этого, прежде чем решать задачу, подвергнем анализу заданные поверхности.

Нетрудно видеть, что грани призмы перпендикулярны горизонтальной плоскости проекций, следовательно, всякая линия граней, в том числе и линия пересечения поверхностей, совпадает с горизонтальным очерком призмы. Очевидно, в этом случае удобнее вспомогательные секущие плоскости выбрать ортогональными плоскости π1. Каждая грань призмы пересекает поверхность полусферы по дуге окружности, которые пересекаются между собой в точках встречи ребер призмы с полусферой. Грань АВ параллельна фронтальной плоскости, значит дуга окружности 1222 проецируется на эту плоскость без искажения. Тогда и вспомогательные плоскости выберем параллельными этой грани.

Отметим, что фронтальные проекции линии пересечения двух других граней – дуги эллипсов, точки которых и будем определять.

Алгоритм решения. Обычно построения начинают с отыскания проекций характерных точек: высшей, низшей, ближней, дальней и др.

1) Определим сначала ближнюю и дальние точки, для чего грань А1В1 проведем плоскость Р1, которая пересекает полусферу по окружности радиуса . Отметим проекции 12 и 22 точек встречи ребер грани АВ с полусферой.

2)Через ребро С1 проведем плоскость Р2 (Р2 ║ Р1, Р2 э С). Получим проекцию 32 точки встречи ребра С.

3)Плоскость Р3, проведенная через центр полусферы О1, даст проекции 42 и 52 точек, которые делят линии пересечения на видимую и невидимую части.

4)для построения проекций верхних точек эллипсов вспомогательные плоскости проведем через точки пересечения пер-

пендикуляров, опущенных из О1 на грани А1С1 и В1С1. каждая плоскость пересекает призму по образующей, а полусферу по ду-

44

ге окружности. Отметим точки 62				и 72: 62= сi c	, п	2	,
72= сi c	, т	2	.Остальные промежуточные точки линии пересе-

чения построены аналогично. Соединим полученные проекции точек и получим пространственную линию пересечения поверхностей, фронтальная проекция которой состоит из трех ветвей, а горизонтальная – совпадает с горизонтальным очерком призмы.

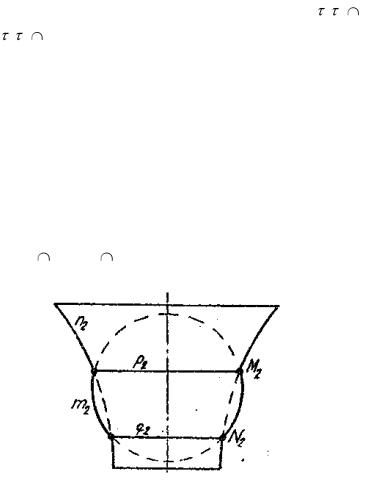
Пересечение соосных поверхностей вращения

Если оси поверхностей вращения совпадают, то линиями их пересечения могут быть только общие параллели (окружности), которые описывают точки пересечения меридианов заданных поверхностей (рис. 1.52).

Таких точек всего две:

М=т п, N=т п, и столько же соответствующих им линий пересечения – р(р2) и q(q2).

Рис. 1.52. Пересечение соосных поверхностей

Пересечение поверхностей вращения, оси которых имеет общую точку (способ концентрических сфер).

Особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных секущих поверхностей использовать сферы, соосные с данными поверхностями.

Способ получил название – способ концентрических сфер.

45

Для использования вспомогательных концентрических сфер необходимо выполнение следующих условий:

1)пересечение двух поверхностей вращения;

2)оси поверхностей – пересекающиеся прямые, параллельные одной из плоскостей проекций, т.е. имеется общая плоскость симметрии, или одна из осей – проецирующая прямая, а вторая – линия уровня (также имеется плоскость симметрии);

3)нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях. Последний пункт не обязателен, так как способ концентрических сфер зачастую дает более легкое решение, чем

способ вспомогательных секущих плоскостей.

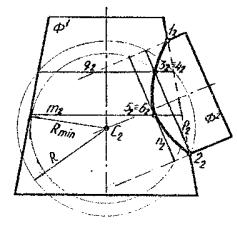
Пусть даны проекции Ф1 (усеченный конус вращения) и Ф2

(цилиндр вращения) на плоскости π2, параллельной их осям, пересекающимся в точке С2 (рис. 1.53).

Рис. 1.53. Способ концентрических сфер

Алгоритм решения.

1)точка С2 пересечения поверхностей принимается за центр вспомогательных сфер.

2)Каждая сфера, соосная и с Ф1 и Ф2, пересекает заданные

поверхности по окружностям. Их проекции на π2 вырождены прямыми линиями, перпендикулярными осям поверхностей. Так,

46

прямые q2 и p2, - фронтальные проекции тех параллелей, по которым сфера радиуса R пересекает Ф1 и Ф2.

3)точка 32и 42 пересечения проекций построенных параллелей принадлежат проекции искомой линии пересечения.

4)Отметим, что прямая т1 – проекция на П2 линии пересечения поверхности Ф1 сферой радиуса Rmin.

5)Пересечение главных меридианов (очерковых образую-

щих) определяет крайние точки 12 и 22.

Частные случаи пересечения поверхностей

В общем случае две поверхности второго порядка пересекаются по пространственной кривой линии четвертого порядка, которую называют биквадратной кривой.

В некоторых случаях биквадратная кривая распадается на две плоские кривые второго порядка (причем одна из них может быть мнимой). Знание подобных частных случаев пересечения поверхностей может быть полезным при решении практических задач. Опуская доказательства, приведем некоторые теоремы и проиллюстрируем их на примерах.

Теорема 1. Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту плоскость в виде кривой второго порядка.

Пример, где выполняются условия этой теоремы, представлен на рисунке 1.53 действительно, плоскость симметрии обязательно должна иметься по условию применения способа концентрических сфер. Фронтальная проекция линии пересечения является параболой.

Теорема 2. Если две поверхности второго порядка пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.

На рис. 1.51 изображены фронтальные проекции Ф2 – сферы и Q2 – эллиптического цилиндра, имеющих общую окружность т2 с центром О2.

47

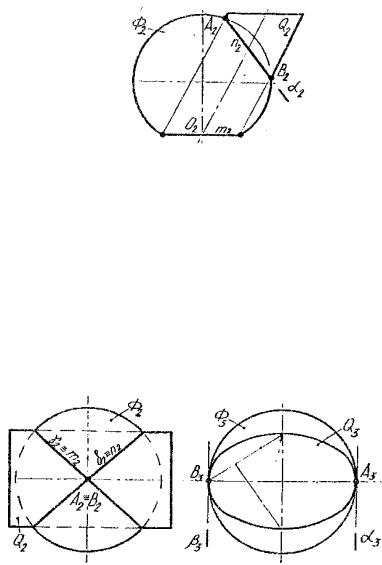
Рис. 1.51. Пересечение сферы и эллиптического цилиндра

Алгоритм решения

Общая окружность радиуса R – одна из плоских кривых второго порядка распавшейся линии пересечения.

Вторая кривая, плоскость α2 которой перпендикулярна π2, проецируется в виде отрезка прямой п2. Для его построения воспользуемся точками А2 и В2, инцидентными очерками заданных поверхностей. Плоская кривая п – окружность.

Теорема 3 (о двойном касании). Если две поверхности второго порядка имеют в двух точках А и В, то линия их пересечения распадается на две плоские кривые второго порядка, плоскости которых проходят через отрезок прямой АВ, соединяющий точки касания. На рисунке 1.52 приведен пример применения этой теоремы.

Рис. 1.52. Построение линии пересечения поверхностей второго порядка

48

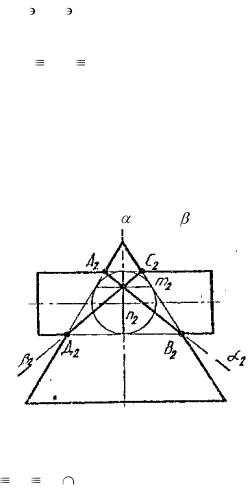
Сфера Ф пересекается с поверхностью эллиптического цилиндр Q по двум окружностям т и п.

А и В – точки касания, через которые проходят касательные плоскости: α А, β В.

Окружности, на которые распалась линия пересечения поверхностей, расположены во фронтально проецирующих плоскостях 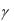и b: 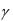т,b п.

Теорема 4 (теорема Монжа). Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.

В соответствии с этой теоремой линии пересечения цилиндра и конуса, описанных около сферы, будут плоскими кривыми

– эллипсами, фронтальные проекции которых изображаются прямыми А2В2 и С2Д2; АВ 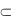, СД 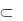(рис. 1.53).

Рис. 1.53. Построение линии пересечения конуса и цилиндра

п2 – проекция линии касания (окружность) сферы и цилиндра. т2 – проекция линии касания (окружность) сферы конуса.

К2 М2 п2 т2 .

Теорема Монжа находит эффективное применение на практике, например, при конструировании трубопроводов. Возможность вписывать сферы в цилиндры одинакового диаметра позволяет быстро запроектировать их пересечение.

49