MP_praktikumNG

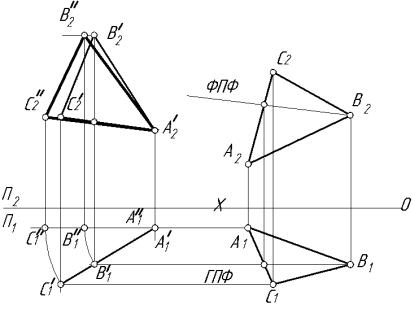
Определение натуральной величины плоской фигуры

Пример 31

Определить натуральную величину ∆ АВС способом вращения

(рис. 2.31).

Рис. 2.31.

Алгоритм решения

Показаны две стадии поворота ∆ АВС, расположенного в плоскости общего положения, с целью получения натурального вида этого треугольника. Действительно, он в последнем своем положении параллелен пл. π2 и, следовательно, проекция А2''В2''С2'' представляет собой натуральный вид треугольника. Чтобы получить такое положение, надо предварительно повернуть плоскость так, чтобы эта плоскость оказалась перпендикулярной к пл. π1. А для этого надо взять фронталь и повернуть ее до перпендикулярности к π1. при этом повороте подразу-

80

мевается ось вращения, перпендикулярная к пл. π2; поэтому горизонтальная проекция треугольника сохраняет свой вид и величину. При втором повороте, приводящем треугольник в параллельное пл. π1 положение, фронтальная проекция при повороте сохраняет вид и величину, полученные во второй стадии поворота, точки А, В и С перемещаются в плоскостях, параллельных пл. π1.

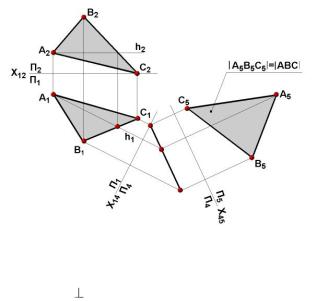
Пример 32

Определить натуральную величину ∆ АВС общего положения способом замены плоскостей проекций (рис. 2.32).

Рис. 2.32

Алгоритм решения

1. Проведем горизонталь. Введем дополнительную плоскость проекций π4 к горизонтали. Проекция треугольника на π4 превращается в прямую линию.

2.Вводим дополнительную плоскость проекций π5 // А4С4.

3.Проекция ∆ АВС на π5 есть натуральная величина. Плоскость общего положения преобразовать в плоскость

уровня заменой только одной плоскости проекций нельзя, так как плоскость π4, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.

81

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций.

Вначале плоскость необходимо преобразовать в проецирующую, а затем проецирующую плоскость преобразовать в плоскость уровня. На рис. 2.32. показано преобразование плоскости ∆ АВС в горизонтальную плоскость уровня. Преобразуйте плоскость общего положения во фронтальную плоскость уровня (исходный чертеж задайте самостоятельно).

Пересечение многогранника плоскостью

При пересечении многогранника плоскостью в сечении получается плоская фигура (называется сечением). Построение сечения необходимо начинать с характерных точек, произвольные точки строят в последнюю очередь.

Задачу по определению сечения многогранника сводят к задаче пересечения прямой с плоскостью (способ граней) или к задаче пересечения прямых (способ ребер).

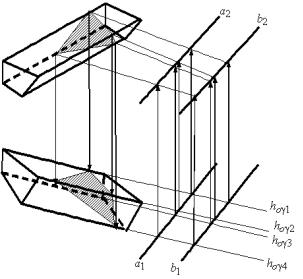
Пример 33

Построить пересечение четырехгранной призмы с плоскостью α (a // b) (рис. 2.33).

82

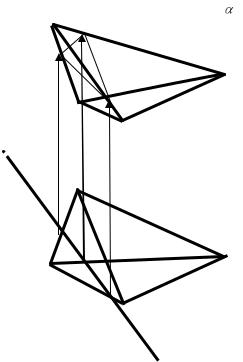
Рис. 2.33

Алгоритм решения

1. Заключим ребра призмы в горизонтально-проецирующие плоскости h0α1, h0α2,h0α3,h0α4.

2.Найдем точки пересечения h0α1, h0α2,h0α3,h0α4 с плоскостью

α(a // b).

3.Найдем точки пересечения этих прямых с ребрами на фронтальной проекции.

4.Соединим эти точки и получим сечение на фронтальной проекции призмы.

5.Построим горизонтальную проекцию сечения.

Пример 34

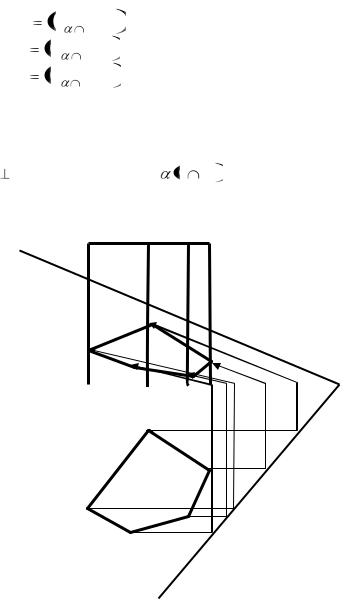
Определить сечение трехгранной призмы SABC горизонтально проецирующей плоскостью α, заданной следами ho (рис. 2.34).

S2	N2
М2	B2
А2	K2

С2

H0α

A1

М1

В1

S1 N1

K1 С1

83

				Рис. 2.34.
			Алгоритм решения
	M1	ho	S1A1 ;
	N1	ho	S1B1 ;
	K1	ho	S1C1 ;
	Построили точки. М2, N2, K2.
	Соединив их получим искомое сечение.
				Пример 35.
	Определить сечение 5-гранной призмы ABCDE , ребра ко-
торой	x секущей плоскостью				h	f (рис. 2.35).
		А2	B2	Е2	D2	C2
				52
		12				42
			22			Xα
	x				32
			B1≡51
					C1≡41
		A1≡11			D1≡31
			E1≡21
84

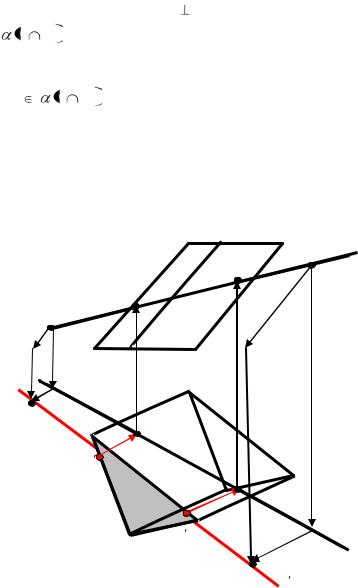
Рис. 2.35.

Алгоритм решения

	Так как ребра призмы			оси x , то точки их пересечения
с	h	f	совпадают с горизонтальными проекциями ребер
( A1, B1,C1, D1, E1).
	Решение сводится к нахождению недостающей проекции
точки		h	f .

Пересечение многогранника прямой

Задача пересечения многогранника прямой сводится к известной схеме пересечения прямой плоскостью. Если многогранник выпуклый, то прямая пересекает многогранник в двух точках.

Пример 36

Найти точки пересечения прямой l с призмой (рис. 2.36). l2

С2

А2

x

А1

A1

C1

C1

l1 85

l1

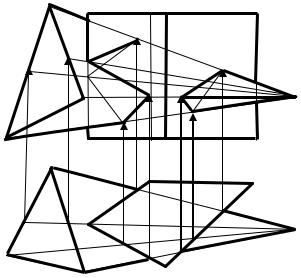
Рис. 2.36.

Алгоритм решения

Проведем косоугольное проецирование (параллельно ребрам призмы). Проекция призмы на π1 совпадает с проекцией основания призмы. Проекция прямой. l1→l11// ребрам призмы. А, B - точки пересечения прямой призмы. Определяем видимость прямой методом конкурирующих точек.

Пересечение многогранников

				Пример 37
	Построить линию пересечения прямой призмы и
наклонногой пирамиды.
	B
				72
6
						22
82				52		D2
	С2			32
				12
x А2
	B1
				71		21
	61≡81			11		D1
	А1		41	31
		С1		51
				Рис. 2.37
		Алгоритм решения

Точки 1, 2, 3 находим как пересечение ребер с гранью призы.

Получим сечение 1-2-3. Для построения сечения 4-5-6-7-8, необходимо провести вспомогательную горизонтально проецирующую плоскость через крайнее левое ребро призмы.

86

Находим точкипересечения этой плоскости с гранями пирамиды (т. 6 и т. 8). Точки 4, 5, 6, 7 получим на пересечении ребер пирамиды с гранями призмы. Определим видимость призмы и пирамиды.

87

Построение линии пересечения поверхностей Пример 38

Определение линии пересечения тел вращения способом секущих сфер (рис. 2.38).

41

42	51	1

2

x	52	32	1

21	12
11	22

31 1

Рис. 2.38

Алгоритм решения

Сначала на проекциях отметим очевидные общие точки (1, 2). Затем вводим вспомогательные плоскости частного положения –

фронтальные , , . Они пересекают фигуры по параллелям 1, 1, 1 . На фронтальной проекции вспомогательные плоскости пересекают сферу в виде концентрических окружностей

88

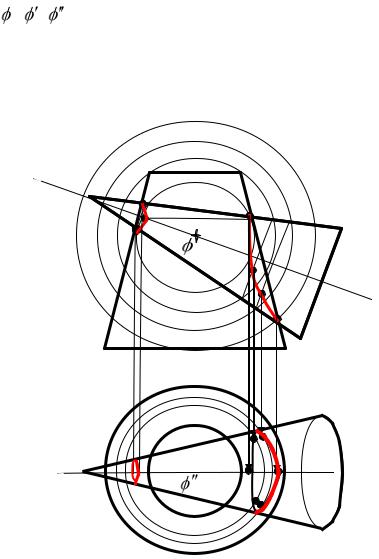
2 , 2 , 2 . На пересечении этих окружностей и восстановлен-
ных из точек горизонтальной проекции цилиндра находятся точ-
ки пересечения поверхностей (3, 4, 5). Полученные точки соеди-
няем плавной кривой.
Пример 39
Построить пересечение поверхности усеченного конуса с
конусом способом концентрических сфер (рис. 2.40).
		32
2		21
		O1
		11
x
		O2
		42
		41
2		31
	Рис. 2.40
Алгоритм решения

89