MP_praktikumNG

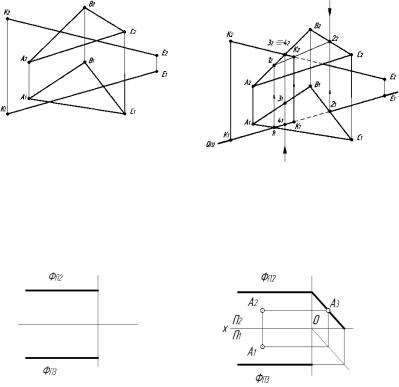
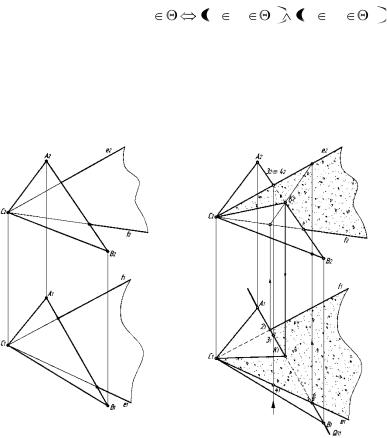
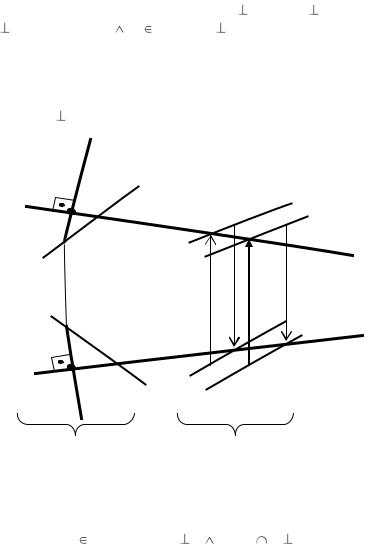
Для определения видимости прямой ЕК относительно плоскости треугольника АВС воспользуемся методом конкурирующих точек. Например точки 3, 4 лежат на скрещивающихся прямых АВ и ЕК, поэтому на фронтальной проекции эти точки проецируются в одну точку, а горизонтальные проекции этих точек лежат на разных проекциях прямых АВ и ЕК.

По направлению взгляда ближе к глазу наблюдателя точка 4, лежащая на прямой ЕК, следовательно, на фронтальной проекции прямая ЕК будет видима до встречи с т. К, а прямая АВ будет расположена за ней. Видимость прямой ЕК относительно плоскости треугольника АВС на горизонтальной проекции определяется аналогично (рис. 2.19, б).

а

б

Рис. 2.19

Пример 20

В плоскости построить точку А, отстоящую от плоскости π1 на 8 мм (рис 2.20).

а

б

Рис. 2.20

70

Алгоритм решения

Достаточно построить профильный след плоскости и отложить на нем т. A3 провести горизонтальную проекцию f1 прямой

принадлежащей плоскости Θ; найти ее фронтальную проекцию f2

и на ней отметить т.A2. A	A	f	1	A	f	2	2
	1	1		2

(рис. 2.20. б)

Прямая и плоскость. Пересечение прямой с плоскостью

Пример 21

Определить линию пересечения двух плоскостей. Видимую часть треугольника АВС оттенить (рис. 2.21. а).

Условие

Решение

а

б

Рис. 2.21

Алгоритм решения

Способ нахождения линии пересечения двух плоскостей заключается в том, что определяют точки пересечения двух прямых, принадлежащих одной из плоскостей с другой плоскостью. Для этого прямая АВ заключается во вспомогательную проецирующую плоскость на горизонтальной проекции. Определяются точки 11-21 пересечения вспомогательной плоскости с прямыми

71

С1 е1 и С1 f1 на горизонтальной проекции. На фронтальной проекции строится вспомогательная прямая 12-22 и определяется т.К2 пересечения вспомогательной прямой с ребром А2В2, которая является искомой точкой пересечения двух плоскостей. Затем определяется горизонтальная проекция т. К2. Видимость плоскостей определяется методом конкурирующих точек (рис. 2.21. б).

	Пример 22
Построить плоскость	перпендикулярную к прямой а и

проходящую через т. А (рис. 2.22).

Рис. 2.22

Алгоритм решения

Через т. А проводим горизонталь h02 и фронталь f01. Чтобы плоскость γ была a , находим две другие проекции h01 и f02 Плоскость γ (h f)

a (рис. 2.22).

Пример 23.

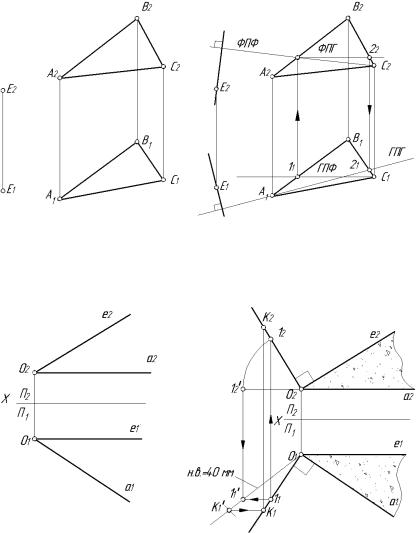
Через т. Е провести прямую линию, перпендикулярную плоскости треугольника АВС (рис. 2.23. а).

Алгоритм решения

Горизонтальная проекция перпендикуляра к плоскости перпендикулярна к горизонтальной проекции ее горизонтали, а фронтальная проекция перпендикуляра к плоскости перпендикулярна к фронтальной проекции ее фронтали. Следовательно, если провести из точки С фронтальную прямую (ГПФ) С111 и определить ее фронтальную проекцию (ФПФ), то искомым перпендикуляром будет перпендикуляр (рис. 2.23. б).

72

а	б

Рис. 2.23

Пример 24

Из т. О восстановить к плоскости перпендикуляр ОК длиной 30 мм (рис. 2.24. а).

а

б

Рис. 2.24

Алгоритм решения

73

На рис.2.24. а задана плоскость определяемая двумя пересекающимися прямыми Оа и Ое. Причем Оа является горизонталью, а Ое фронталью. Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Но чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к одноименной проекции какой либо прямой этой плоскости, прямая должна быть прямой уровня. У перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная перпендикулярная к фронтали. Следовательно, перпендикуляром к плоскости будет прямая ОК, перпендикулярная на горизонтальной проекции к О1а1, а на фронтальной проекции строим О2К2 перпендикулярную к О2е2. Затем способом вращения определяем натуральную величину перпендикуляра и откладываем на нем натуральную величину 30мм (рис. 2.24. б).

Пример 25.

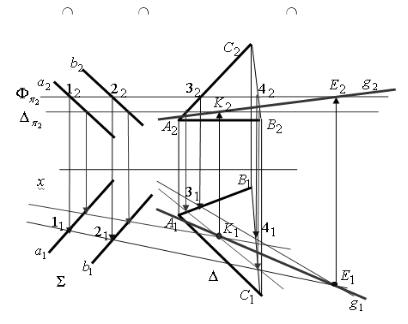
Построить линию пересечения двух заданных плоскостей. Σ (а b), Ω (AB AC), определить q (Σ Ω) , (рис.2.25).

Рис. 2.25

74

Алгоритм решения

1) Выбирают произвольно секущую вспомогательную горизонтальную плоскость Ф, которая пересекает Σ и Ω по точкам 1, 2, 3, 4. Ф пересекает заданные плоскости по прямым 1-2 и 3-4. точка их пересечения К.

2) Вводим вторую секущую плоскость , аналогично находим точку т. Е; ЕK - есть искомая линия пересечения двух заданных плоскостей.

Пример 26

Построить линию пересечения двух плоскостей, заданных треугольниками. Определить видимость линии пересечения

(рис.2.26).

Рис.2.26

Алгоритм решения

Строим пересечение двух сторон одного треугольника с плоскостью второго. Через D1E1 проводим горизонтально-проецирующую плос-

75

кость 1 . Определим пересечение

с ABC . Т. M - точка пересе-

чения сторон DE с ABC . Аналогично находим точку N - пересечения

1 (проходящую через прямую Е1К1).

После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она может быть определена с помощью фронтально конкурирующих точек. Для определения видимости на горизонтальной плоскости проекций используют горизонтально конкурирующие точки. Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность плоскостей. При этом следует учесть, что у параллельных плоскостей две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Пример 27

Задана плоскость Σ (AB BC). В т. В восстановить перпендикуляр к BK (рис.2.27). Σ

	h1
	B2
A2	K1
	C2

x

B1

f2

A1

h2

К2

С1

Рис. 2.27

76

Алгоритм решения

Проведем h и f (горизонталь и фронталь). Проекции перпендикуляра BK к плоскости Σ составляют прямой угол с гори-

зонталью и фронталью плоскости: B2K2 h2; B1K1			h1. Так как
BK двум прямым f0	h0 Σ, то она плоскости Σ.
Следствие: плоскости, проходящие через BK, перпендику-
лярны Σ.
		Пример 28
Задана плоскость	α (m // n) и прямая a. Через a провести
плоскость β α (рис.2.28).
l1
	а1
x		m1	A2
		n1
			h1

fo2		A1	m2	f2
				f1
h2	n2
а2
l2		β
		Рис. 2.28
	Алгоритм решения
Через плоскость α. проводим горизонталь h и фронталь f и
выбрав точку A	α, проводим l h f. β (a l) α (m // n).

77

Пример 29

Определить двугранный угол между плоскостями (рис. 2.29)

Рис. 2.29

Алгоритм решения

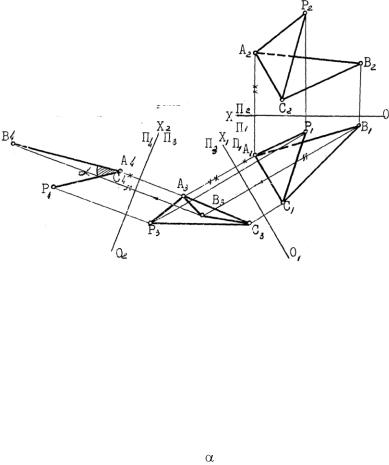
Решение производится способом перемены плоскостей проекций. Для этого достаточно общее ребро между плоскостями спроецировать в точку, что возможно только при замене двух плоскостей. Первый раз меняем плоскость π2 на π3,установив еѐ параллельно общему ребру АС, затем производим вторую замену, на этот раз плоскости π1; на плоскость π4, установив еѐ перпендикулярно ребру АС. В новой системе π3/π4, на плоскости π4 получим искомый двугранный угол при ребре пирамиды АС в натуральную величину.

Пример 30

Задан ∆ АВС и точка А. Определить расстояние от точки А до плоскости ∆ АВС (рис. 2.30).

Алгоритм решения

78

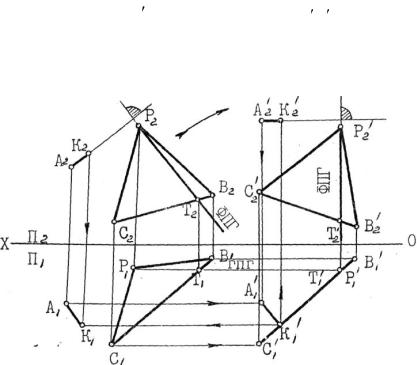
Решим задачу способом вращения вокруг оси, перпендикулярной плоскости проекции с одновременным плоскопараллельным перемещением. В нашем случае выберем ось вращения, проходящую через точку Р, перпендикулярную фронтальной плоскости проекций. Повернѐм плоскость ∆ ВСР вокруг этой оси до положения проецирующей плоскости. Вращение производим до тех пор, пока фронталь этой плоскости не станет перпендикулярно к плоскости проекции π1, что характерно для горизонтально проецирующей плоскости. Одновременно перемещаем и т. А, не изменяя еѐ проекции относительно перемещаемого треугольника. В результате треугольник на горизонтальную плоскость π1 спроецируется в прямую С1P1В1. Тогда очевидно, что перпендикуляр, опу-

щенный из точки А1 на эту прямую (отрезок А1К1) и будет истин-

ной величиной расстояния от вершины пирамиды А до грани ВСР, т.е. искомой высотой. Для лучшего усвоения задачи находим положение перпендикуляра АК в первоначальных проекциях. Направление построения показано стрелками (рис. 2.30).

Рис. 2. 30

79