Лекции Соболева часть 3

88

Лекции 10 - 11

∞

∑(un +

un

)= (u1 +

u1

)+(u2 +

u2

)+…+(un +

un

)+…

(3)

n=1

для него справедливо неравенство 0 ≤ un +

un

≤ 2

un

,

n =1, 2,….

Ряд ∑∞ (2 un ) сходится из условия сходимости ряда (2);

n=1

Ряд (3) сходится на основании первого признака сравнения. Ряд (1) есть разность двух сходящихся рядов

∞	∞					∞
∑un	= ∑(un	+		un		)−∑		un		и, следовательно, сходится.
n=1	n=1					n=1

!Обратное утверждение неверно.

ОСходящийся ряд, для которого ряд, составленный из абсолютных

величин его членов, также сходится, называется абсолютно схо-

дящимся.

Заметим, что доказанный признак сходимости достаточен, но не необходим: существуют знакопеременные ряды, для которых ряды, составленные из абсолютных величин их членов, расходятся.

ОСходящийся ряд, для которого ряд из абсолютных величин его членов расходится, называется условно сходящимся.

Пример:

∞

(−1)

n−1

1

(−1)

1. Знакочередующийся ряд ∑

=1 −

1

+

−…+

(1) сходит-

n

n

n=1

2

3

1

1

ся условно по признаку Лейбница (см. ниже), так как

>

и

n −1

1

n

lim

= 0,

но соответствующий ряд из абсолютных величин членов

n→∞ n

∞

1

данного ряда (1) является гармоническим ∑

и расходится.

n

n=1

∞

n−1

1

1

2. Ряд ∑

(−1)

=1 −

+

+… сходится абсолютно, так как этот

2

2

2

n=1

n

2

3

знакочередующийся ряд сходится по признаку Лейбница (см.

ни-

∞

1

же), и ряд ∑

сходится тоже.

2

n=1

n

Числовые ряды

89

11.3. Знакочередующиеся ряды. Признак Лейбница

ОРяд называется знакочередующимся, если его члены являются (поочередно) положительными и отрицательными.

Такой ряд можно записать в виде

∞

∑(−1)n−1 un = u1 −u2 +u3 −…+(−1)n−1 un +…,	(1)
n=1

где un > 0 для любого n (если первый член ряда отрицателен, то

∞

исследуют ряд −∑(−1)n−1 un ).

n=1

ТПризнак Лейбница. Если в знакочередующемся ряде (1):

1)	абсолютные величины членов ряда монотонно убывают,
u1 > u2 > u3 >….,
2)	lim un = 0, то а) ряд (1) сходится; б) его сумма S > 0 положитель-
	n→∞

на и не превосходит первого члена ряда, то есть, S < u1 .

Доказательство:

Рассмотрим последовательность четных частичных сумм знакочередующегося ряда (1):

S2 = u1 −u2 , S4 = (u1 −u2 )+ (u3 −u4 )…, S2n = (u1 −u2 )+(u3 −u4 )+(u2n−1 −u2n ).

Каждая из разностей, стоящих в скобках, положительна по условию теоремы, значит, S2 n > 0 и последовательность S2n является

возрастающей.
Если записать эту сумму в виде S2n = u1 −(u2 −u3 )−	(u4 −u5 )−…−u2n,
то каждая из разностей в скобках положительна и	S2n < u1, , т.е. по-

следовательность S2n ограничена сверху.

Итак, последовательность S2n является возрастающей и ограничена

сверху, следовательно, имеет предел lim S		2n	= S, причем 0 < S < u .
	n→∞			1
Последовательность нечетных частичных сумм				S2n+1 = S2n +u2n+1 . Пе-
реходя к пределу, имеем lim S2n+1	= lim S2n + lim u2n+1 = S , следовательно,
n→∞	n→∞	n→∞

lim Sn = S , ряд (1) сходится.

n→∞

Признак Лейбница используется для приближенного вычисления суммы знакочередующегося ряда с определенной точностью. Сумма

отброшенных членов знакочередующегося ряда Лейбница по абсолютной величине не превосходит первый отброшенный член.

Пример:

∞	(−1)	n+1
Сколько членов ряда нужно взять, чтобы сумму ряда ∑		= S
n=1	n

	90							Лекции 10 - 11
		найти с точностью до 0,001?						S = Sk +δ ,
		Представим сумму ряда в виде:
		∞	∞
		где Sk = ∑un , δ =	∑un				по признаку Лейбница.
		n=1	n=k +1
		По условию, uk +1	=		1		< 0,001,	откуда k > 999, нужно взять 1000
				k	+	1
		членов ряда.

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

определения ряда, суммы ряда, частичной суммы ряда; необходимый и достаточный признак сходимости ряда (критерий Коши); необходимый признак сходимости ряда; теоремы сравнения рядов с положительными членами;

достаточные признаки сходимости числовых рядов с положительными членами: признак Даламбера, признак Коши, интегральный признак сходимости; исследование знакопеременных рядов, абсолютная сходимость;

знакочередующиеся ряды, признак Лейбница.

Лекции 12 – 14 ФУНКЦИОНАЛЬНЫЕ РЯДЫ

В лекциях 12 – 14 рассматриваются функциональные ряды и важнейшая их разновидность – степенные ряды. При достаточно широких предположениях относительно функции ее можно представить как сумму некоторого функционального ряда, причем математические операции над этим рядом (сложение, умножение, предельный переход, почленное дифференцирование и интегрирование) совершаются по тем же простым правилам, что и одноименные операции над конечными суммами. Подобная простота применения и легкость получения конкретных результатов обусловливает широкое применение функциональных рядов в математике и ее приложениях.

12.Функциональные ряды

12.1Равномерная сходимость

12.2.Признак Вейерштрасса

13.Степенные ряды

13.1.Вычисление радиуса сходимости

13.2.Свойства степенных рядов

13.3.Разложение функций в степенные ряды Тейлора и Маклорена

13.4.Разложение элементарных функций в ряды Маклорена

13.5.Применение степенных рядов

14.Ряды в комплексной области

14.1.Числовые ряды с комплексными членами

14.2.Степенные ряды в комплексной области

12.Функциональные ряды

Пусть функция fn (x), n N определена в области D, x D

ОВыражение вида

			∞
			∑ fn (x)= f1 (x) + f2 (x) +…+ fn (x) +…					(1)
			n=1
называется функциональным рядом.
∞		x		x		x
Например, ∑Sin			= Sin x + Sin		+…+ Sin		+…. .
		n				n
n=1			2
При x = x0 D	из функционального					ряда (1) получается числовой
ряд			∞
							(x0 )+…
			∑ fn (x0 ) = f1 (x0 )+ f2					(2)

n=1

92	Лекции 12 - 14

ОЕсли для x0 D числовой ряд (2) сходится, то точка x0 называется

точкой сходимости функционального ряда (1). Если в каждой точ-

	∞
ке	x D1 D числовые ряды ∑ fn (x) сходятся, то функциональный
	n=1

ряд(1) называется сходящимся в области D1 .

ОСовокупность всех точек сходимости образует область сходимости функционального ряда (1).

Рассмотрим частичные суммы функционального ряда (1):

Sk (x)= f1 (x)+ f2 (x)+…+ fk (x).

Ряд (1) сходится к функции f (x) в области сходимости, если пре-

дел последовательности его частичных сумм lim Sk (x)= f (x).

k →∞

Пример:

Найдите область сходимости ряда

x (− ∞, ∞).

∞

1

1

1

1

∑

=

+

+…

+…,

2n

1

+ x

2

1 + x

4

2n

n=1 1

+ x

1 + x

Если

x

<1,

то

lim u

n

= lim

1

=1 ≠ 0,

ряд расходится, так как не

n→∞

n→∞ 1 + x2n

x = ±1,

выполняется необходимый признак сходимости ряда;

если

∞

ряд

∑1 =

1

+

1

+… расходится;

если

x

>1:

1

<

1

-

беско-

2n

2n

n=1 2

2

2

1

+ x

x

нечно убывающая геометрическая прогрессия.

∞

1

Сравнение

со

сходящимся

рядом ∑

при

x

>1

дает область

2n

n=1 x

сходимости исследуемого ряда x (−∞, −1) (1, ∞).

12.1. Равномерная сходимость

Пусть lim Sn (x)= f (x). По определению предела это означает, что для

n→∞

любого x из области сходимости, например, x0 и x1 , выполняются условия:

1)	x = x0 D1 : ε > 0 N0 (ε ), n > N0		Sn (x0 )− f (x0 )				ε ;
2)	x = x1 D1 , x0 ≠ x1 : ε > 0 N1 (ε ), n > N1				Sn (x1 )− f (x)				> ε .

Заметим, что числа N0 и N1 , вообще говоря, различны.

ОФункциональный ряд, сходящийся для всех x D1 из области сходимости, называется равномерно сходящимся в этой области, ес-

Функциональные ряды							93
ли ε > 0		существует не зависящий от x					номер N (ε), такой, что при
n > N (ε)	выполняется неравенство			Rn (x)		< ε	для всех x из области сходи-
		∞
мости,	где	Rn (x)= ∑ fk (x)− остаток ряда.

k =n+1

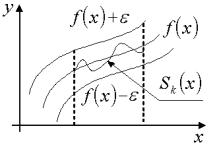
Геометрический смысл равномерной сходимости заключается в следующем: Если окружить график функции y = f (x)

” ε	-	полоской”, определяемой					соотноше-
нием		f (x)−ε > y > f (x)+ε,	x [a,b], то гра-
фики всех функций Sk (x), начиная с доста-
точно большого k , целиком лежат в этой ”
ε	-	полоске”, окружающей			график пре-
дельной функции y = f (x).									(−1)n+1
	Покажем, что ряд		1		−		1	+…		+… сходится равномерно
			x2 +1			x4 + 2			x2n + n
при всех x(− ∞ > x > ∞).

По признаку Лейбница этот ряд сходится и его остаток можно оценить следующим образом:

Rn (x)

<

un+1

(x)

,

Rn (x)

<

1

<

1

,

1

≤ ε, n ≥

1

−1.

x2n+2

+ n +1

n +1

n +1

ε

1

Возьмем

N =

−1, тогда для n ≥ N

Rn (x)

< ε

для x из области сходимо-

ε

сти, значит ряд равномерно сходится.

		∞
О	Функциональный ряд ∑ fn (x)		называется мажорируемым в неко-
		n=1
	торой области	изменения x ,	если существует					такой сходящийся
		∞
	числовой ряд ∑un с положительными членами,							что для всех	x из
		n=1			fn (x)
	этой области	выполняются	неравенства				≤ un , n =1,2,…..		Ряд

∞

∑un

n=1

∞

называется мажорантой ряда ∑ fn (x).

n=1

12.2. Признак Вейерштрасса (признак равномерной сходимости функционального ряда)

Функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

94

Лекции 12 - 14

∞

(1)

∞

(2) в силу ограниченности

Например, для рядов ∑an sin nx,

∑an cos nx

n=1

n=1

функций выполняется

an sin nx

≤

an

,

an cos nx

≤

an

.

∞

По признаку Вейерштрасса, если ряд ∑an сходится абсолютно, то ря-

n=1

ды (1), (2) сходятся равномерно на промежутке.

Теоремы о почленном интегрировании и дифференцировании функциональных рядов

			∞
Т	Пусть ряд ∑ fn (x)= f (x) с непрерывно дифференцируемыми членами
			n=1
			∞
	сходится для x [a,b] и ряд ∑ fn′(x) сходится равномерно на				a,b		, то-
	гда ∑ fn (x)		n=1
			сходится равномерно, его сумма дифференцируема и
	∞		∞
	[S(x)]′ = ∑ fn′(x), т.е. ряд ∑ fn (x) можно дифференцировать почленно.
	n=1		n=1
			∞
Т	Пусть ряд ∑ fn (x)= f (x) равномерно сходится на [a,b], тогда:
			n=1
	1) этот ряд можно почленно интегрировать на этом отрезке и
	∞	b	b
	2) ряд ∑	∫ fn (x)dx = ∫ f (x)dx сходится равномерно.
	n=1 a		a

Пример:

Найдите сумму ряда ∑∞ (n2 + 9n + 5)xn+1 = f (x).

n=0

Для нахождения суммы ряда воспользуемся известной формулой для суммы геометрической прогрессии

∞	1
∑xn =1+ x + x2 +…=		,		x		<1 .
	1− x
n=0

(1)

Дифференцируя левую и правую части формулы (1), получим последовательно

∞

n−1

′

∞

n−2

″

∑nx

1

∑n(n

−1)x

1

=

,

=

.

1− x

n=1

(2)

1

− x

n=2

Заменим в формулах (2) индекс суммирования:

1 ′

∞

n

1

″ ∞

n

= ∑(n +1)x

,

= ∑(n +

2)(n +1)x

.

1

− x

n=0

1

− x

n=0

Выделим в сумме, подлежащей вычислению, слагаемые, пропорциональные первой и второй производной:

Функциональные ряды

95

∞

∞

∑(n2 + 9n +5)xn

+1 = ∑((n + 2)(n +1)+ 6(n +1)−3)xn+1 =

n=0

n=0

∞

∞

∞

= x

∑(n + 2)(n +1)xn + 6∑(n +1)xn −3∑xn =

n=0

″

1 ′

n+0

n=0

1

1

x

+6

−

3

.

1− x

1− x

1

− x

Вычислим производные:

1 ′

1

1

″

1

1

=

,

=

=

,

(1

− x)2

− x)2

(1 − x)3

1

− x

1 − x

(1

f (x)

2

6

3

−3x3 + 5x

тогда

= x

+

−

=

.

(1 − x)3

(1 − x)2

(1 − x)3

1 − x

13. Степенные ряды

ОФункциональный ряд вида

	∞
	∑an (x − x0 )n = a0 + a1 (x − x0 )+ a2 (x − x0 )2 +…			(1)
	n=0
	называется степенным по степеням (x − x0 ).
	В частности, при x0 = 0 ряд
	∞
	∑an xn = a0 + a1 x + a2 x2 +…			(2)
	n=0
	является степенным по степеням x .
	Ряд (1) сводится к ряду (2) заменой (x − x0 )→ x ,	a0 ,	a1 ,	a2 …- коэф-
	фициенты ряда. Ряд (2) сходится по крайней мере в одной точке:
	при x = 0 S = a0 .
Область сходимости степенного ряда. Теорема Абеля			(x0	≠ 0), то он
	∞	x0
Т	1) Если степенной ряд ∑an xn сходится в точке

n=0

абсолютно сходится для x : x < x0 , причем на отрезке x ≤ R < x0 сходимость будет равномерной.

96	Лекции 12 - 14

2) Если степенной ряд расходится в точке x0′ (x0′ ≠ 0), то он расходится и для всех x таких, что x > x0′ .

Доказательство:

1)

Пусть

∞

тогда

lim an x0 n = 0 последовательность

∑an x0 n сходится,

n=0

n→∞

an x0 n ограничена M :

an x0 n

< M .

∞

Рассмотрим

ряд

∑an xn ,

запишем

его

в

виде:

n=0

x

2

x 2

x

x

2

a0

+ a1 x0

+…

и сравним с рядом M + M

+ M

+…, ко-

x0

+ a2 x0

x0

x0

x0

торый представляет собой при x < x0 геометрическую прогрессию

x

∞

g =

<1,

т.е. сходится,

следовательно, ряд

∑an xn абсолютно схо-

x0

n=0

дится, т.к.

an xn ≤ M

x

n .

x0

При этом

на отрезке

x

≤ R <

x0

сходимость равномерная, т.к.

∞

R

n

сходится мажорирующий числовой ряд ∑M

.

x0

n=0

∞

2) Пусть ряд ∑an (x0′ )n расходится. Докажем,

что он расходится при

n=0

′

∞

x :

x

>

x0′

.

От противного: пусть x :

x

>

x0

и ряд ∑an xn

сходится,

n=0

следовательно, по 1-ой части теоремы Абеля ряд бы сходился в

точке x0	′			′						, что противоречит условию.
		т.к.	x0		<		x

С

1). Областью сходимости степенного ряда является симметричный

интервал с центром в точке О.

2). Существует граница между точками сходимости x0 и расходи-

мости x 0′ : R = S u p {

x 0

} = in f {

x 0′

}.

Число R такое, что при

x

< R ряд сходится, а при

x

> R - расходит-

О

ся, называется радиусом сходимости степенного ряда, а интервал

x (− R, R) - интервалом сходимости.

Функциональные ряды

97

В граничных точках x = ±R поведение ряда требует дополнительного исследования.

∞

Для ряда ∑an (x − x0 )n интервал сходимости имеет вид x (x0 − R, x0 + R) с

n=0

центром в точке x0 :

13.1. Вычисление радиуса сходимости

Степенные ряды в области сходимости сходятся абсолютно и можно использовать признаки сходимости рядов с положительными членами.

1.По признаку Даламбера:

lim

u

n+1

(x)

= lim

an+1

x

n+1

=

x

lim

a

n+1

<1,

сходится,

un (x)

n

расходится.

n→∞

n→∞

an

x

n→∞

an

>1,

an

1

Ряд сходится, если

x

<

1

.

R =

= lim

.

a +

a

a

n→∞

lim

n+1

lim

n+1

n 1

an

an

n→∞

n→∞

2.По признаку Коши:

lim n

un (x) = lim n

an x

n

= x lim n an

<1, сходится,

n→∞

n→∞

n→∞

>1, расходится.

Ряд сходится,

если

x <

1

.

R =

1

lim n

an

lim n an

n→∞

n→∞

Пример:

∞

x

n

∞

x

n

Найдите область сходимости рядов: 1)

∑

и 2) ∑

.

n

n!

n=1

n=1

1)

R =

1

= lim

an

= lim

n +1

=1. .

a

a +

n

n→∞

n→∞

lim

n+1

n 1

an

n→∞