Лекции Соболева часть 3

108	Лекции 12 - 14

x0 x1 x2

an

a5

: 2a2 = 0 → a2 = 0;

: 6a3 = 2 + 4 → a3 =1;

:12a4 = 4a2 + 4a2 → a4 = 0;

……

=2an−2 n −1

……

= 24 = 12 , a6 = 0,…. y = x + x3 + 12 x5 +….

14. Ряды в комплексной области

14.1. Числовые ряды с комплексными членами

Пусть zn = an + ibn , n N - последовательность комплексных чисел.

	∞	(1) называется числовым рядом
О	Выражение ∑zn = z1 + z2 +…+ zn +…

n=1

вкомплексной плоскости.

ТРяд (1) сходится, если существует конечный предел

S =limS		n	z	=lim (a +ib )+(a +ib )+…+(a +ib ) =
		=lim
n→∞	n	n→∞∑ k		n→∞	1 1	2 2	k x
		k=1
	n	n		= A+iB,
=lim ∑ak +i∑bk
n→∞ k=1		k=1

где A и B - пределы соответствующих частичных сумм рядов, составленных из действительных и мнимых частей чисел zn .

Необходимым и достаточным условием сходимости ряда (1) явля-

					∞	∞
	ется одновременная сходимость числовых рядов ∑an					и ∑bn	с дей-
					n=1	n=1
	ствительными членами.
	∞
Т	Если сходится положительный ряд ∑		zn		, составленный из модулей

n=1

членов ряда (1), то ряд (1) так же сходится. Напомним, что

eiϕ = cosϕ + i sinϕ, eiϕ = cos2 ϕ + sin2 ϕ =1. z = x +iy = x2 + y2.

Функциональные ряды

109

Пример:

Исследуйте на сходимость ряды:

∞

iπn

∞

∞

n

e

(−

1)

1) ∑

=

∑(cosπn + i sinπn)= ∑

сходится условно.

n

n

n=1

n=1

n=1

∞

e

iπ

n

2)

∑

сходится абсолютно, поскольку

n

2

n=1

1

∞

1

а)

zn

=

, ряд ∑

сходится абсолютно;

2

2

n

n=1 n

∞

iπ

∞

cos π

∞

sin π

∞

cos π

∞

sin π

б) ∑

e

n

= ∑

n

+ i∑

n

, ряды ∑

n

и

∑

n

сходятся

2

n

2

n

2

n

2

n

2

n=1 n

n=1

n=1

n=1

n=1

∞

1

абсолютно по теореме сравнения со сходящимися рядом ∑

,

2

n=1

n

π

sin

π

так как

cos n

≤

1

;

n

≤

1

.

n2

n2

n2

n2

∞

n

n + 2i

3.

∑=

(1 + i)n +

3

n

1

z

n + 2

n

(n + 2i)n

(n2 + 4)n 2

=

=

=

=

n

(1 + i)n +

3

((1

+ i)n + 3)n

((n + 3)2 + n2 )n 2

n

2

+ 4

n 2

=

Сравним полученный ряд со сходящимся рядом

2

2n

+ 6n + 9

.

∞

1 n 2

∞

1

∑

=∑

,

который

представляет

собой

бесконечно

( 2 )

n

n=1

2

n=1

убывающую геометрическую прогрессию:

n

2

+ 4

n 2

2

+ 6n +

9

lim

2n

=1,

исследуемый ряд сходится абсолютно.

1 n 2

n→∞

2

∞

n

3

2n + 5

∞

n

3

4.

+ i

ряд

∑

сходится по при-

∑

2

n

3n

2

− 2n

расходится, т.к.

2

n

n=1

n=1

un+1

(n +1)3 2n

1

∞

2n + 5

знаку Даламбера

, а ряд

∑

= lim

n+1

3

=

<

2

lim

un

2

n

2

1

3n

− 2n

n→∞

n→∞

n=1

расходится по признаку сравнивания с гармоническим рядом ∑∞ 1 :

n=1 n

110

Лекции 12 - 14

(2n

+ 5)n

=

2

lim

3n2

− 2n

3

n→∞

∞

(2

+ i)

n

n

5.

∑

расходится, так как

2n

n=1

(

5 )n n

(2

+ i)n n

5

n

z

=

=

=

n → ∞ .

n

2n

2

n

2

∞

(1

+ i)

n

n

2

n

2nn

= n n .

6.

∑

сходится абсолютно, так как

zn

=

2n

n=1

2

2

		∞	n
	Ряд	∑		сходится
			n
		n=1	2

lim	(n +	1) 2 n
		n+1
n→∞	2		n
	∞		1
7. ∑
	n=1	(n −i)

= 12 <1.

n	= ∑n=1 (n2n++1)i	n
	∞

по признаку Даламбера:

сходится абсолютно, так как

n

2

1

n

2

+1

1

12

zn

=

+ (n2 +1)2 n

=

(n2 +1)2 n

=

.

(n2 +1)2 n

(n2

+1)n

Сравнивая

этот

ряд

со

сходящимся

рядом

1

12

n3

12

,

lim

=1 , убеждаемся,

что исследуемый ряд схо-

(n2

n3

n→∞

+

1)n

дится абсолютно.

14.2. Степенные ряды в комплексной области

ОСтепенным рядом в комплексной области называется ряд вида

∞	(z − z0 )n = a0 + a1 (z − z0 )+ a2	(z − z0 )2 +...,
∑an			(1)
n=0
где ai (i N ) u z0	- фиксированные комплексные числа, z = x + iy		- не-
зависимая комплексная переменная.
	∞
При z0 = 0 ряд принимает вид ∑an zn		= a0 + a1z + a2 z2 +...	2)

n=0

Функциональные ряды

111

ОПусть z1 - некоторое комплексное число. Ряд (1) сходится в точке z1 , если при подставке в него вместо z числа z1 , получается сходящийся ряд с комплексными членами. В противном случае ряд (1) расходится.

ТТеорема Абеля. Если степенной ряд (1) сходится в точке z1 , то он сходится, и притом абсолютно, в любой точке z1 , которая лежит внутри окружности с центром z0 , проходящей через z1 , т.е. для

всех z таких, что z − z0 < z1 − z0 .

ОМножество точек z, в которых ряд сходится, называется областью сходимости ряда.

Для степенных рядов (1) возможны случаи: 1) ряд сходится только при z − z0 (R = 0);

2)ряд сходится при всех z(R = ∞);

3)существует такое число R>0, что ряд сходится при любом значении

z, для которого z − z0 < R и расходится при любом z, для которого z − z0 > R . Число R называется радиусом сходимости степенного ряда (1), а круг z − z0 < R называется кругом сходимости ряда.

На границе области сходимости z − z0 = R ряд

может как сходиться, так и расходиться.

Для ряда (2) областью сходимости ряда является круг z < R радиуса R с центром в начале коорди-

нат.

Радиус сходимости: по признаку Даламбера:

R =

1

= lim

an

,

a

a

n→∞

lim

n+1

n+1

n→∞

an

по признаку Коши:

1

R =

.

lim n

a

n→∞

n

112

Лекции 12 - 14

Пример:

Найдите области сходимости рядов

∞

1)

∑(z − z0 )n =1 + (z − z0 )+ (z − z0 )2 +...

R=1

Ряд

сходится внутри

n=0

круга

z − z0

<1 и расходится вне этого круга. В точках окружности

z − z0

=1 ряд расходится,

т.к. его общий член не стремится к ну-

лю.

∞

n

z

2

z

3

n +1

2)

∑

z

= z +

+

+... R = lim

=1. Ряд сходится внутри кру-

n→1

n

2

3

n→∞

n

га

z

<1 и расходится вне этого круга. На граничной окружности

z

=1 в некоторых точках

(z = −1) сходится,

а в некоторых (z =1)

расходится.

∞

z

2

z

3

n!

3)

∑

z

= z +

+

+...

R = lim

= ∞ Ряд сходится, при том

(n −1)!

n=1

n!

2!

3!

n→∞

абсолютно, при любом z.

n!

1

∞

∑n!z n =1!z + 2!z 2 + 3!z3 +...

R = lim

= lim

= 0

n=1

n→∞ (n +1)!

n→∞ n +1

Ряд сходится только в точке z0 = 0 .

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

определение функционального ряда, точки сходимости ряда, области сходимости ряда; понятие равномерной сходимости, признак Вейерштрасса;

степенные ряды, их область сходимости, вычисление радиуса сходимости; разложение функций в степенные ряды Тейлора и Маклорена; ряды Тейлора и Маклорена основных элементарных функций;

применение степенных рядов (вычисление значений функций, вычисление интегралов, не берущихся в элементарных функциях, решение дифференциальных уравнений).

Лекции 15 - 16 РЯДЫ ФУРЬЕ

При описании периодически повторяющихся явлений более естественными являются разложения изучаемых функций не в степенные ряды, а в ряды по функциям, также обладающим свойством периодичности. В лекциях 15 – 16 рассмотрены тригонометрические ряды Фурье, широко использующиеся при исследовании периодических функций.

15.1.Гармонический анализ. Ряды Фурье

15.2.Ортогональные системы функций

15.3.Тригонометрические ряды

15.4.Коэффициенты Фурье и ряд Фурье для периодической функции с периодом 2π

15.5.Разложение функций в тригонометрические ряды

16.1.Разложение в ряд четных и нечетных функций с периодом 2π

16.2.Ряд Фурье для функции с произвольным периодом Т=2L

16.3.Разложение в ряд Фурье непериодических функций

16.4.Комплексная форма ряда Фурье

16.5.Интеграл Фурье

15.1.Гармонический анализ. Ряды Фурье

О

Гармоническим колебанием называется периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса.

ООсновной гармоникой называется простейшая периодическая функция вида (x ) = a s i n ) = ), где− ϕ 0+ ϕ 0f x x aa c o s (ω(ωy = –

амплитуда, ω - круговая частота, ϕ0 - начальная фаза колебания.

Если независимая переменная - время t, то величина у=f(t) совер-

	шает			гармоническое колебание с периодом T =			2π	и	частотой
							ω
		1			ω
	υ=			=		.
		T
					2π
	Функции a2 (sin 2ωx +ϕ0 ), a3 sin (3ωx +ϕ0 ), ... называются								второй,

третьей, … высшими гармониками относительно основной.

114	Лекции 15 - 16

Основная гармоника может быть представлена в виде суммы двух тригонометрических функций одного и того же аргумента:

a sin (ωx +ϕ0 )= a sin ωx cosϕ0 + a cosωx sinϕ0 = Asin ωx + B cosωx .

Функции sin x и cos x являются периодическими с периодом T = 2π .

Функции sin 2x и cos 2x , sin 3x и cos3x ,… так же имеют период 2π .

Любая линейная комбинация вида

a0 + a1 cos x +b1 sin x + a2 cos 2x +b2 sin 2x +...

(1)

так же является периодической с периодом T = 2π .

Гармонический анализ используется для изучения периодических процессов. Любая величина f (t ), связанная с периодическим процес-

сом, по истечении периода T возвращается к своему первоначальному значению, т.е. является периодической функцией с периодом T .

Сущность гармонического анализа заключается в представлении функций, описывающих периодические процессы, в виде конечной или бесконечной суммы гармонических колебаний вида (1); гармонический анализ состоит в разложении периодических функций в сходящийся ряд Фурье.

15.2. Ортогональные системы функций

Предварительно докажем следующие утверждения, которые следует знать для дальнейшего изложения.

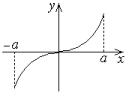
1). Интеграл от нечетной функции в симметричных пределах равен нулю. Если f(x)=-f(-x), то

∫a	f (x)= ∫0	f (x) dx + ∫a	f (x)dx =
−a	−a	0

замена х на (-х) в первом интеграле дает

= ∫0 f (x)dx + ∫a f (x)dx = ∫0 f (−x)dx + ∫a f (x)dx = −∫a f (x)dx + ∫a f (x)dx = 0 .

−a

0

a

0

0

0

Ряды Фурье

115

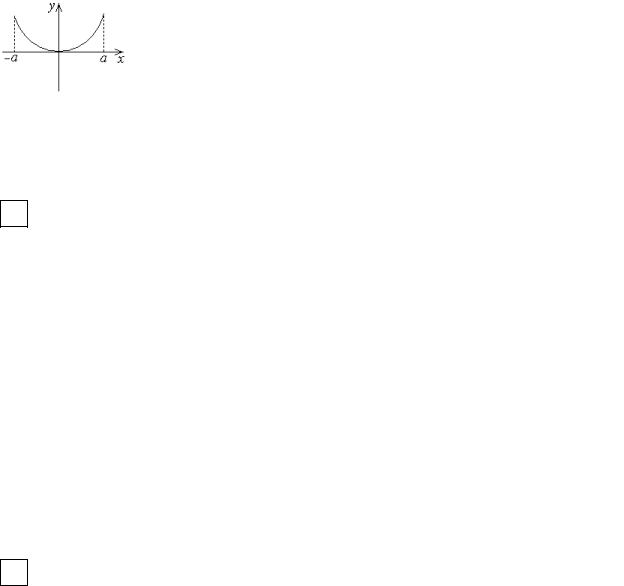
2). f(x)=f(-x) – четная функция.

∫a f (x)dx = ∫0 f (x)dx + ∫a f (x)dx =

−a

−a

0

Заменяя х на (-х) в первом интеграле, получим

= −∫0 f (−x)dx + ∫a f (x)dx = ∫a f (x)dx + ∫a f (x)dx = 2∫a f (x)dx.

a

0

0

0

0

!Если функция f(x) имеет период 2π, то интеграл от нее по любому отрезку длины 2π имеет одно и то же значение, т.е.

			a+∫2π	f (x)dx = 2∫π			f (x)dx.			(٭)
			a			0
Имеем a+∫2π	f (x)dx = ∫0		f (x)dx +		2∫π	f (x)dx +		2π∫+a	f (x)dx	(٭٭)
a		a			0			2π		x = 2π +t, тогда
Заменим в		последнем		интеграле			правой части

2π∫+a f (x)dx = ∫a f (2π + t )dt = ∫a f (t )dt в силу периодичности f(x).

2π 0 0

Отсюда следует, что сумма первого и третьего интегралов в правой части (**) равна нулю.

Пусть функции f1 (x) и f2 (x) заданы на отрезке x [a,b,], а произведение этих функций f1 (x) f2 (x) интегрируемо на этом отрезке.

ОФункции f1 (x) и f2 (x) называются ортогональными на отрезке

[a,b], если ∫b	f1 (x)f2 (x)dx = 0.
a
Рассмотрим систему периодических тригонометрических функций
	{	}	.
с периодом 2π : cos0 =1, cos x, sin x, cos 2x, sin 2x, ... cos nx, sin nx,...

Покажем, что эти функции ортогональны на отрезке [−π, π], а значит, в силу утверждения 3 и на любом отрезке [a, a + 2π].

Для доказательства нужно вычислить и убедиться, что интегралы

π∫sin nxdx = 0,	π∫cos nxdx = 0,	π∫cos mxsin nxdx = 0,
−π	−π	−π
π∫cos mx cos nx dx = 0 при m ≠ n ,			π∫sin mxsin nxdx = 0 при m ≠ n .
−π			−π

Действительно,

116									Лекции 15 - 16
	π		cos nx					π
1)	∫	sin nx dx = −							= 0 в силу нечетности подынтегральной
	−π		n					−π
	функции;					π
2)	π∫	cos nx dx = sin nx						=	1 (sinπn −sin (−πn))= 0 , так как sinπn = 0 .
	−π		n			−π			n
3)	π∫sin nx cos nx dx =			1 π∫sin 2nx dx = 0 в силу нечетности подынтеграль-
	−π			2 −π

ной функции.

С использованием формул:

cos nxcos mx = 12 cos(n + m)x + cos(n − m)x ;

sin nxsin mx = 12 cos(n − m)x −cos(n + m)x ; sin nx cos mx = 12 sin (m + n)x + sin (m − n)x .

Вычислим следующие интегралы:

4)

π

sin nx sin mx dx =

1

π

(

cos (n

−m)x −cos (n + m)x dx =

∫

∫

)

−π

2 −π

1

sin

(

n −m

)

x

sin

(

n + m

)

x

π

=

−

= 0, так как sin Rπ = 0.

2

n −m

n + m

−π

π

1

π

5)

cos nx cos mx dx =

cos

(n −m)x +cos (n + m)x dx =

∫

∫ (

2

)

−π

−π

1

sin

(n − m)x

sin (n + m)x

π

=

+

= 0 .

2

n − m

n + m

−π

π

1

π

(

6)

sin nx cos mx dx =

sin (n

+ m)x +sin (n −m)x dx = 0

∫

∫

2

)

−π

−π

в силу нечетности подынтегральной функции системы.

Итак, ортогональность γ тригонометрических функций доказана.

Вычислим значения интегралов при m=n:

7) π∫

−π

π

8) ∫

−π

sin

2

nx dx =

1

π

(1 −cos 2nx)dx =

1

sin 2nx

π

1

(π +π )=π ;

2 −∫π

2

x −

2n

=

2

−π

2

1

π

(1 +cos 2nx)dx =

1

sin 2nx

π

1

(π +π )=π .

cos

nx dx =

−∫π

2

x +

2n

=

2

2

−π

Ряды Фурье

117

15.3. Тригонометрические ряды

ОФункциональный ряд вида:

a0 + a1 cos x +b1 sin x + a cos 2x +b2 sin 2x +... = a0		∞
		+ ∑(an cos nx +bn
2	2	n=1
называется	тригонометрическим рядом,	а постоянные
an , bn , (n =1,	2, 3...) называются коэффициентами ряда.

sin nx)

числа

15.4.Коэффициенты Фурье и ряд Фурье для периодической функции с периодом 2π

ТЕсли f(x) непрерывная периодическая функция с периодом 2π, интегрируемая на интервале (-π, π), такая, что для всех х справедливо разложение

		a0	∞
	f (x)=		+ ∑(an cos nx +bk sin nx),	(1)
	2		n=1

и ряд сходится к f(x) равномерно, то для коэффициентов ряда справедливы формулы Фурье:

a

=

1

π

f

(

x dx,

a =

1

π

f

(

x

)

cos nx dx,

b =

1

π f

(

x

)

sin nx dx

∫

π

∫

π

0

π

)

n

n

∫

−π

−π

−π

Доказательство:

Так как ряд (1) сходится к f(x) равномерно, то его можно интегри-

ровать почленно:

π

f

x dx =

π

a0

dx +

∞

π

a cos nx dx + π b sin nx dx

(2)

∫

(

∫

∑ ∫

)

2

n

∫

n

−π

−π

n=1 −π

−π

В п. 15.1. показано, что

π∫ an

cos nx dx = 0,

π∫bn sin nx dx = 0 .

−π

−π

Значит, из (2)

π∫ f (x)dx = π a0 ,

откуда a0

=

1

π

f (x)dx.

(3)

∫

−π

π

−π

Умножим ряд (1) почленно на cos kx и проинтегрируем:

π

a0

π

∞

π

π

∫ f (x)cos kx dx =

∫cos kx dx +∑

an ∫cos nx cos kxdx +bn ∫sin nxcos kx dx

,

−π

2

−π

n=1

−π

−π

так как все интегралы кроме того, для которого n = k , равны нулю, (см. п. 15.1.), получаем: