
Лекции Соболева часть 3
.pdf
48 |
Лекция 5 - 9 |
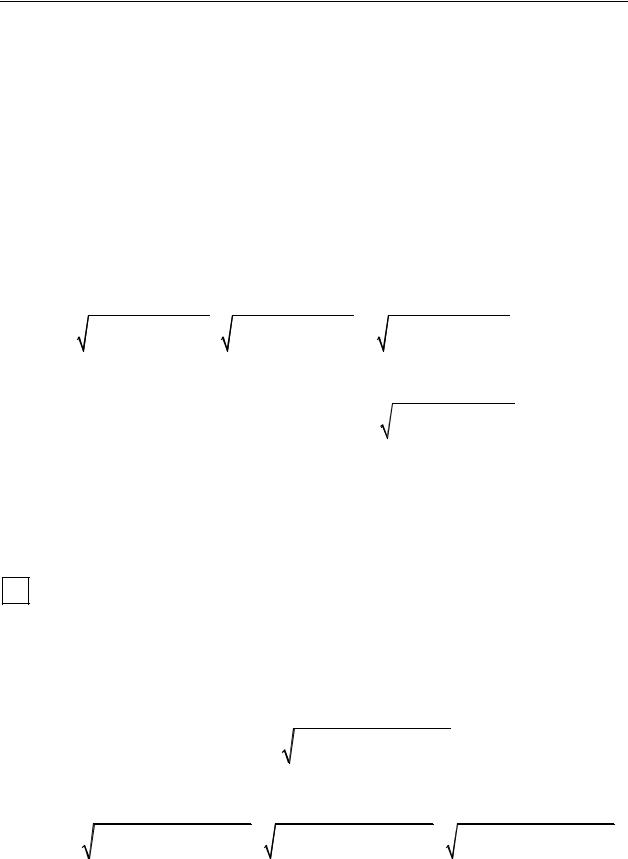
ОЕсли этот предел существует и не зависит от способа разбиения поверхности Σ на участки Σi и от выбора точки Pi , то он называется потоком векторного поля a = a (P ) через поверхность Σ.
П = ∫∫(a dσ) = ∫∫adσ = |
|
n |
|
lim |
∑(a(Pi ) ∆σ ). |
||
Σ |
Σ |
max(∆σ )→0 i=1 |
|
ОИспользуя введенное ранее понятие поверхностного интеграла второго рода, можно определить поток вектора a через поверхность Σ как поверхностный интеграл второго рода от вектора a по поверхности Σ.
!Поток вектора a - скалярная характеристика векторного поля.
7.2. Свойства потока
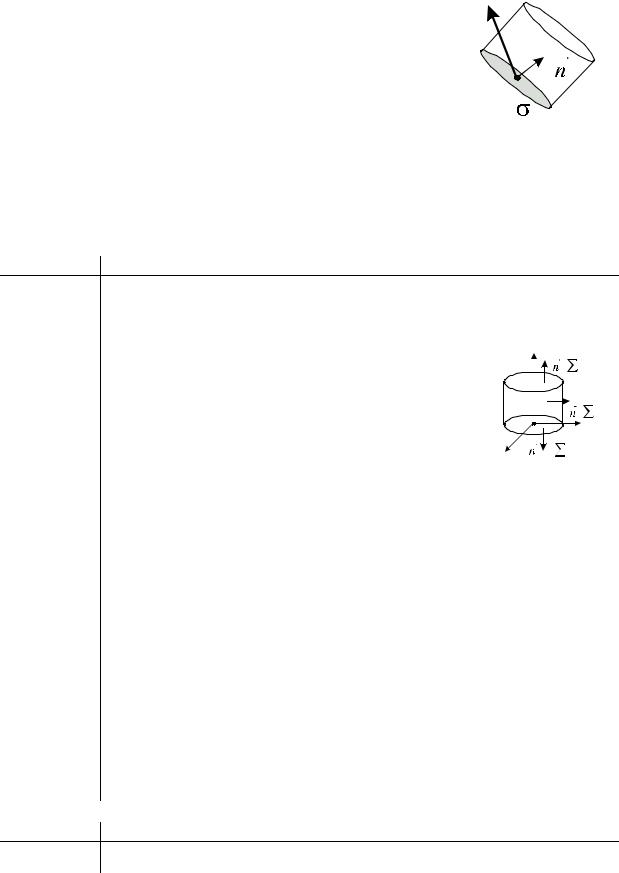
1.Поток меняет знак на обратный с изменением ориентации поверхности
Σ: ∫∫(a, dσ) = −∫∫(a, dσ) .
Σ+ Σ−
2.Свойство аддитивности по отношению к области интегрирования. Если поверхность Σ состоит из нескольких гладких частей: Σ1, Σ2 , ..., Σn , то
поток векторного поля a равен сумме потоков поля a через поверхности:
|
n |
n |
|
Σ1, Σ2 , ..., |
Σn : П = ∑Пi = ∑∫∫(a, dσ) |
|
|
|
i |
i Σ |
|
|
|
i |
|
3. Свойство линейности |
∫∫(αia + βia)dσ =αi∫∫(a, dσ) + βi∫∫(a, dσ) , |
||
|
Σ |
Σ |
Σ |
где α и β - некоторые постоянные.
7.3. Вычисление потока
Если ввести |
dσ = n0dσ |
- векторный диффе- |
|
ренциальный элемент поверхности, то |
0 |
||
|
|
|
|
(a dσ )= (a n0dσ )= (a n0 )dσ , |
|
||
∫∫(a dσ) =∫∫(a n0 )dσ = ∫∫(Прn0 a) dσ . |
0 |
||
|
|
|
|
Σ |
Σ |
Σ |
xy |
Таким образом, по данной формуле поток сводится к интегралу 1-го рода по поверхности Σ от ска-
49
a (P) на нормаль n0 (P ) к этой поверхности
Σ (иначе: от проекции поля a (P) на нормаль к поверхности n0 (P ) ).
7.3.1. Проектирование на одну координатную плоскость
Пусть поверхность Σ задана явно уравнением z = f (x, y) и однозначно проектируется в область Dxy на координатной плоскости Oxy .
|
|
{ |
|
′ |
′ |
} |
0 |
|
|
n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда |
n = |
|
f |
, f |
|
,−1 |
, n |
= ± |
|
n |
= |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fx′ |
|
|
|
|
|
|
|
|
|
|
fy′ |
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ± |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;− |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
( fx′)2 +(fy′)2 +1 |
|
( fx′)2 +( |
fy′)2 +1 |
( fx′)2 +(fy′)2 |
+1 |
|
|||||||||||||||||||
и поток вектора a = a(P)= a(x, y, z ) через эту поверхность равен |
||||||||||||||||||||||||||
∫∫(a, n0 )dσ = ∫∫(a, n0 ) |
|
|
dxdy |
|
|
= ∫∫(a, n0 ) |
( fx′)2 +(f y′)2 +1 dxdy = |
|||||||||||||||||||
|
|
cos(γ ) |
|
|
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
Σ |
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ±∫∫(ax (x, y, f (x, y)) fx′+ ay (x, y, f (x, y)) fy′ − az (x, y, f (x, y))) dxdy ,
Dxy
т.е. вычисление потока сводится к вычислению двойного интеграла. Знак зависит от направления нормали к поверхности.
!Аналогичные формулы получаются при проектировании на другие координатные плоскости для поверхностей вида x = f ( y, z) и y = f (x, z) .
7.3.2. Проектирование на три координатные плоскости |
|
|
|
|
|
|
|||||||||
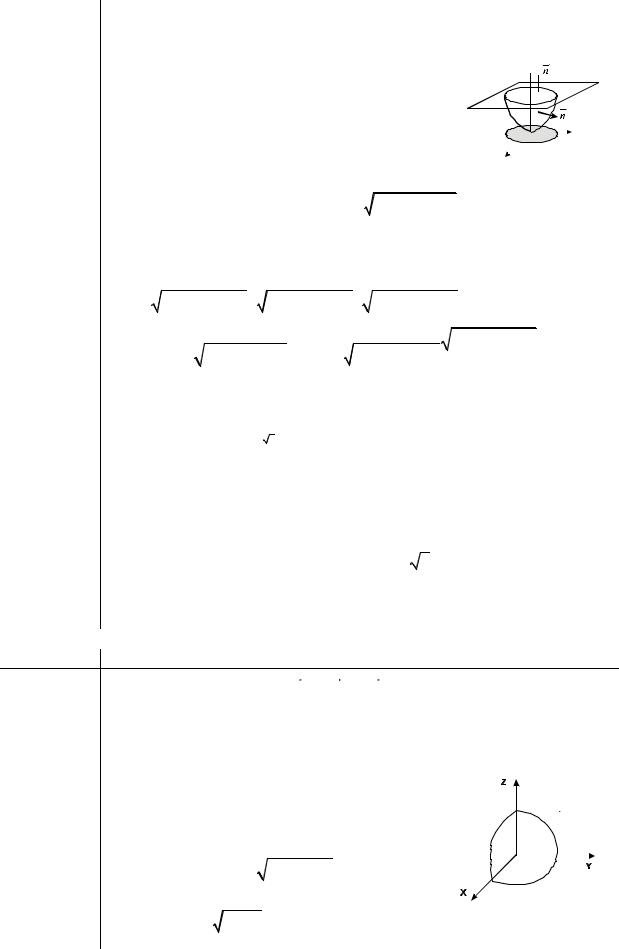
Пусть поверхность Σ задана (неявно) уравнением F (x, y, z)= 0 ; |
|
||||||||||||||
|
n ={Fx′, Fy′, Fz′}, |
|
n |
|
= (Fx′)2 +(Fy′)2 +(Fz′)2 , n0 = ± |
|
|
n |
|
|
= |
|
|||
|
|
|
|
||||||||||||
|
|
|
|
|
n |
|
|
|
|||||||
|
|
|
|
||||||||||||
F ′ |
|
|
|
Fy′ |
|
|
|
|
|||||||
|
|
|
|
F′ |
|||||||||||
|
; |
|
|
|
|||||||||||
= ± |
x |
; |
|
|
|
|
|
|
z |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(Fx′)2 +(Fy′)2 +(Fz′)2 |
|
|
|
(Fx′)2 +(Fy′)2 +(Fz′)2 (Fx′)2 +(Fy′)2 +(Fz′)2 |
|
||||||||||
.
Пусть α, β,γ - углы, которые образует нормаль с осями координат. Тогда орт n0 имеет координаты: n0 ={cosα,cos β,cosγ}. Так как a ={ax ,ay , az }, то

50 |
Лекция 5 - 9 |
(a,n0 )= ax cosα + ay cos β + az cosγ
и
∫∫(a, n0 )dσ = ∫∫ax cosαdσ + ∫∫ay cos βdσ + ∫∫az cosγdσ .
Σ Σ Σ Σ
Рассмотрим отдельные слагаемые: ∫∫az cosγdσ . Пусть поверхность Σ опи-
Σ
сывается уравнением z = z(x, y) , тогда, т.к. поле a(P) в поверхностном интеграле берётся в точке P Σ, то для любой его компоненты координата z вы-
ражается |
через x и |
y , az (x, y, z) |
= az (x, y, z (x, y)), dσ = |
dxdy |
, и |
||
cosγ |
|||||||
|
|
|
|
|
|
||
∫∫az cosγdσ = ∫∫az (x, y, z(x, y))cosγ |
dxdy |
= ±∫∫az (x, y, z(x, y))dxdy . |
|
|
|||
cosγ |
|
|
|||||
Σ |
Dxy |
|
Dxy |
|
|
||
Знак (+) соответствует острому углу между нормалью и осью z (cosγ > 0), знак (–) – тупому углу между нормалью и осью z (cosγ < 0).
Аналогично,
∫∫ax cosαdσ = ±∫∫ax (x( y, z), y, z)dydz ,
|
Σ |
Dyz |
|
∫∫ay cos βdσ = ±∫∫ay (x, y(x, z), z)dxdz , |
|
|
Σ |
Dxz |
и окончательно имеем: |
|
|
∫∫(a,dσ) = ±∫∫ax (x( y, z), y, z)dydz ±∫∫ay (x, y(x, z), z)dxdz ± |
||
Σ |
Dyz |
Dxz |
±∫∫az (x, y, z(x, y))dxdy .
Dxy
!1). Знаки перед слагаемыми соответствуют знакам направляющих косинусов нормали cosα,cos β,cosγ .
2). Вычисление потока векторного поля сводится к вычислению трёх двойных интегралов при условии, что поверхность взаимно однозначно проектируется на все три координатные плоскости. Если это не имеет места, поверхность нужно разбить на однозначно проектирующиеся участки.
3). Указанная формула устанавливает связь между потоком и поверхностным интегралом 2-го рода
∫∫(a,dσ) = ±∫∫(ax (x, y, z)dydz +ay (x, y, z)dxdz + az (x, y, z)dxdy) .
ΣΣ
Теория поля |
|
|
51 |
||||||||
7.4. Физический смысл потока |
|
|
|
|
|
||||||
Пусть a(P) - поле скоростей некоторой жид- |
|
|
|
|
|||||||
кости, |
a =V , а Σ - произвольная поверхность в поле, |
|
|
|
|
||||||
тогда: |
(a, dσ ) = (a, n0 )dσ = |
|
V |
|
cosϕ dσ = Прn0V dσ |
- |
|
|
|||
|
|
|
|
|
|
||||||
Pi |
0 |
||||||||||
объём столба жидкости с основанием dσ и высотой |
d |
||||||||||
|
|||||||||||
Прn V , |
т.е. объем жидкости, протекающей через пло- |
|
|||||||||
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
щадку |
dσ в единицу времени в направлении |
n0 . |
|
|
|
|
|||||
Суммируя по поверхности Σ, получаем, что ∫∫(a dσ ) |
- поток жидкости, |
||||||||||
Σ
протекающей через поверхность Σ в единицу времени.
Пример:
Вычислить поток |
векторного |
поля радиус-вектора a = r (x, y, z) |
|
|
через |
|||||||
внешнюю сторону цилиндра (H– высота, R- радиус). |
|
|
|
|
|
|
|
|
||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
a(P) = r ;, Σ = Σ1 Σ2 Σ3 |
|
Z |
|
|
|
|
|
|
3 |
|||
|
0 |
|
|
|
||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
Π = Π1 +Π 2 +Π3 . |
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
0 |
||||||
П2 = ∫∫(a,dσ )= ∫∫(r, n0 )dσ =… |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Y |
||||
|
Σ2 |
Σ2 |
|
X |
0 |
|
|
1 |
|
|
||
{ (r, n0 )= R , из рисунка ясно, что проекция r |
|
|
|
|
|
|
|
|
||||
на |
|
|
|
|
|
|
|
|
||||
нормаль к Σ2 равна R} |
|
|
|
|
|
|
|
|
|
|
||
|
|
…= ∫∫Rdσ = R∫∫dσ = 2π R2 H . |
|
|
|
|
|
|
|
|
||
|
|
Σ2 |
Σ2 |
|
|
|
|
|
|
|
|
|
|
|
П3 = ∫∫(r , dσ )= ∫∫(r , n0 )dσ = … |
|
|
|
|
|
|
|
|
||
|
|
Σ3 |
Σ3 |
|
|
|
|
|
|
|
|
|
{из рисунка ясно, что проекция r на n0 по Σ3 |
равна H, |
|
|
|
|
|
|
|
|
|||
т.е. (a,n0 )Σ |
= H } |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
…= ∫∫Hdσ = H ∫∫dσ = π R2 H .
Σ3 Σ3
П1 = ∫∫(a,dσ )= ∫∫(r,n0 )dσ =0.
Σ1 Σ1
П = П1 + П2 + П3 = 3πR2H.
Пример:
Вычислить поток векторного поля a(P) = y2 j + zk через всю поверх-
52 |
Лекция 5 - 9 |
z = x2 + y2
ность (нормаль внешняя): Σ: .
z = 2.
Решение: |
|
|
|
Разобьем |
поверхность |
на две |
части |
Σ = Σ1 Σ2 |
и представим |
поток в |
виде |
П = П1 + П2 ; |
|
|
|
П1 = ∫∫(a, dσ )= ∫∫(a, n0 )dσ , |
|
||
Σ1 |
Σ1 |
|
|
Z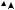 0
0 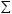 2 П2
2 П2
Z=2
0 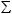 1 П1
1 П1
Y
X
|
|
|
|
|
|
|
|
|
|
|
n0 = ± |
n |
(знак вы- |
|||||||||||||||
a(P) = (0, y2 , z) ; n = (2x, 2 y, −1) , |
n |
= 4x2 + 4 y2 +1 , |
||||||||||||||||||||||||||
n |
||||||||||||||||||||||||||||
бирается «+», так как cos(γ ) < 0 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2x |
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n0 = |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
. |
|
|
|
|
||
4x2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 y2 +1 4x2 + 4 y2 +1 4x2 + 4 y2 +1 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П1 = ∫∫ |
|
2 y3 − z |
|
dσ = |
∫∫ |
|
|
|
2 y3 − z |
|
4x |
2 |
+ 4 y |
2 |
+1dxdy = |
|||||||||||||
|
4x |
2 |
+ 4 y |
2 |
+1 |
|
|
4x |
2 |
+ 4 y |
2 |
+1 |
|
|
||||||||||||||
|
Σ1 |
|
|
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
= ∫∫(2 y3 −(x2 + y2 ))dxdy =… |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
{перейдем в полярную систему координат} |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2π |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
... = ∫ dϕ ∫ ρd ρ(2ρ3 sin3 ϕ − ρ2 ) = ... = −2π . |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П2 = ∫∫(a, dσ )= ∫∫(a, n0 )dσ =... |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Σ2 |
|
|
|
Σ2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
{ n0 = (0;0;1) (a, n0 ) = z } |
|
|
|
|
|
|||||||||||||||||
|
|
|
... = ∫∫zdxdy = 2∫∫ dxdy = 2π( |
|
2)2 = 4π . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
Dxy |
|
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
П = П1 + П2 = −2π + 4π = 2π .
Пример:
Найти поток вектора a = xyi + yz j + xzk через часть сферы
x2 + y2 + z2 =1, расположенную в первом октанте (нормаль внешняя).
Решение:
П = ∫∫ax dydz + ay dxdz + az dxdy
|
Σ |
|
|
|
|
{компоненты поля и области интегрирова- |
|
||||
ния обладают симметрией относительно |
n0 |
||||
замены x → y → z и D yz → Dxy → Dxz } |
|
||||
П = 3∫∫az dxdy = 3∫∫ x 1− x2 − y2 dxdy = |
Dxy |
||||
|
Dxy |
Dxy |
|
||
π / 2 |
1 |
|
3 |
|
|
= 3 ∫ |
dϕ∫ρ cos |
1− ρ2 ρd ρ = |
π . |
|
|
|
|
||||
0 |
0 |
16 |
|
|
|

Теория поля |
53 |
Важно отметить, что cosα, cosβ, cosγ > 0, так как сторона поверхности внешняя, и перед всеми интегралами берется знак (+).
7.5. Дивергенция векторного поля
Дивергенция - это дифференциальная и локальная (зависит от точки) количественная характеристика векторного поля. Пусть вектор-функция
a(P) = ax i + ay j + az k имеет непрерывные частные производные первого порядка по всем переменным.
О Дивергенцией векторного поля a = a(Р) в точке Р(x,y,z) называется
число diva = |
∂a |
|
(x, y, z) |
+ |
∂ay (x, y, z) |
+ |
∂a |
(x, y, z) |
, |
или, опуская аргумен- |
||||||||||
|
|
|
x |
|
∂x |
|
|
|
|
z |
∂z |
|||||||||
|
|
|
|
|
|
∂y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ты: |
diva = |
∂a |
x + |
∂ay |
+ |
∂a |
z . Используя |
оператор |
Гамильтона (набла): |
|||||||||||
|
|
|
∂y |
|
|
|||||||||||||||
|
|
|
∂x |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|||||
= i |
∂ |
+ j |
∂ |
|
|
+ k |
∂ |
|
, дивергенцию можно записать в виде скалярного |
|||||||||||
|
∂y |
∂z |
||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
произведения diva = ( ,a) .
7.5.1. Свойства дивергенции
1.Линейность div(λa + µb) = λdiva + µdivb , где λ и µ - произвольные постоянные.
2.Пусть u = u(x, y, z) - скалярное поле, тогда div(u a) = u diva + (a gradu) . Доказательство:
|
|
|
|
div(u a) = |
∂(u a |
) |
+ |
∂(u ay ) |
+ |
∂(u a |
) |
= |
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
z |
|
||||||||
|
|
|
|
|
|
|
|
∂y |
|
|
|||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
∂z |
|
|
|||
= |
a |
∂u |
+ |
ay∂u |
+ |
a |
∂u |
+u ( |
∂a |
x + |
|
∂ay |
+ |
∂a |
|
)= agradu +u diva . |
|||||
x |
|
|
z |
|
|
|
|
|
|
|
z |
||||||||||
|
∂y |
|
|
|
|
∂y |
|
|
|||||||||||||
|
∂x |
|
|
∂z |
|
∂x |
|
|
|
∂z |
|
|
|
||||||||
Пример:
1). a = r = xi + yj + zk .
divr = ∂∂x x + ∂∂y y + ∂∂z z =1 +1 +1 = 3 .
2). a = (c1 , c2 , c3 ) , diva = ∂∂x c1 + ∂∂y c2 + ∂∂z c3 = 0 .

54 |
Лекция 5 - 9 |
|
7.6. Физический смысл потока через замкнутую поверхность |
||
Рассмотрим замкнутую поверхность Σ, ограни- |
a |
|
чивающую объем G в векторном поле a = a(P) ско- |
||
>0 |
||
ростей течения несжимаемой жидкости. |
0 |
|
Поток вектора a = a(P) через поверхность Σ, |
P2 |
|
a |
||
Π = ∫∫(a,dσ) равен количеству жидкости, протекаю- |
||
P1 <0 |
||
Σ |
||
щей через поверхность Σ в единицу времени. Обо- |
0 |
|
значим единичный вектор внешней нормали n0 . Век- |
|
|
торные линии входят и выходят из замкнутой по-
верхности Σ. В точке P1 угол (a,n0 ) > π2 ; это означает, что жидкость втекает
внутрь поверхности. В точке выхода P2 (a,n0 ) < π2 , следовательно, жидкость
вытекает. Поток векторного поля a через замкнутую поверхность Σ численно равен разности потоков жидкости, втекающей и вытекающей в единицу времени со скоростью a в пространственную область G, ограниченную Σ.
Пусть П>0, следовательно, жидкости вытекает больше, чем втекает, в области G есть источники поля.
Если П<0, втекает жидкости больше, чем вытекает, то в G есть стоки. Если П=0, то в области G источников и стоков или нет, или они компен-
сируют друг друга.
7.7. Теорема Остроградского - Гаусса
Если в некоторой области G трёхмерного про- |
|
странства, ограниченной замкнутой кусочно- |
|
гладкой поверхностью Σ, задано непрерывно диф- |
|
ференцируемое векторное поле a = axi + ay j + azk , |
|
то поток векторного поля a через внешнюю сторо- |
|
ну замкнутой поверхности Σ равен тройному инте- |
X |
Z
|
2 |
|
3 V |
|
1 |
|
Y |
xy |
Г |
|
гралу от функции |
|
∂a |
x + |
∂ay |
+ |
∂a |
|
по области G, |
|
|
|
|
z |
||||
|
∂y |
|
||||||
|
|
∂x |
|
∂z |
|
|||
ограниченной поверхностью Σ: |
|
|
|
|
∂ay |
|
|
|
|
|
|
∂a |
|
|
∂a |
|
|
Π = ∫∫(a dσ) = ∫∫∫ |
|
x + |
|
+ |
|
z dxdydz , |
||
|
∂y |
|
||||||
Σ |
G |
|
∂x |
|
∂z |
|||

Теория поля |
55 |
где символ ∫∫ обозначает интеграл по замкнутой поверхности.
Σ
Доказательство: Часть 1.
Рассмотрим область G, правильную в направлении оси Oz, которую будем называть элементарной Hz областью. Это означает, что снизу и сверху она ограничена поверхностями: Σ1 : z1 = z1 ( x, y) и Σ2 : z2 = z2 ( x, y) соответст-
венно, а сбоку цилиндрической поверхностью Σ3 с образующими, парал-
лельными оси Oz, и направляющей Г. Рассмотрим одно слагаемое:
∫∫∫ |
∂a |
z2 |
∂a |
∫∫dxdyaz (x, y, z) |
|
z2 (x, y) |
|
|
|
||||||
∂zz dxdydz = ∫∫dxdy ∫ |
∂zz dz = |
|
z (x, y) |
= |
|||
G |
Dxy |
z1 |
|
Dxy |
|
1 |
|
|
|
|
|||||
= ∫∫dxdy{az (x, y, z2 (x, y)) − az (x, y, z1(x, y)}=
Dxy
= ∫∫az (x, y, z2 (x, y)) dxdy − ∫∫az (x, y, z1(x, y)) dxdy =…
Dxy Dxy
{на Σ2 cosγ > 0 , а на Σ1 cosγ < 0.
Учитывая, что dxdy = cosγ dσ , получаем:
на Σ2 : dxdy = cosγdσ ,
на Σ1 : dxdy = −cosγdσ } …= ∫∫az (x, y, z)cosγdσ + ∫∫az (x, y, z)cosγdσ =…
|
Σ2 |
Σ1 |
Добавим интеграл по Σ3 |
∫∫az (x, y, z)cosγdσ |
в полученную сумму, так как на |
|
Σ3 |
|
Σ3 cosγ всюду равен нулю, а следовательно, и ∫∫az (x, y, z)cosγdσ = 0 . |
||
|
|
Σ3 |
Тогда |
|
|
…= ∫∫az (x, y, z)cosγdσ + ∫∫az (x, y, z)cosγdσ + ∫∫az (x, y, z)cosγdσ = |
||
Σ2 |
Σ1 |
Σ3 |
= ∫∫ az (x, y, z) cosγdσ = ∫∫az (x, y, z)cosγdσ . |
||
Σ1 +Σ2 +Σ3 |
Σ |
|
Часть 2.
Рассмотрим пространственную область G, которую можно разбить на n
элементарных областей Hz типа, т.е. G = n Gk . Докажем, что и в этом случае
k =1
справедлива теорема Остроградского-Гаусса.
Пусть Σ1(k ) , Σ(2k ) , Σ(3k ) - нижняя, верхняя и боковая части поверхности Σ(k ) , ограничивающей область Gk ,

56 Лекция 5 - 9
тогда
|
|
|
|
|
∫∫∫G |
∂z |
|
n |
∫∫∫G |
|
∂z |
|
|
|
|
|||||
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∂az |
dxdydz = ∑ |
|
|
|
|
|
∂az |
dxdydz = |
|
|
||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
|
∫∫az cosγdσ + ∫∫az cosγdσ + |
∫∫az |
|
|
= ∫∫az cosγdσ , |
||||||||||||||
|
cosγdσ |
|||||||||||||||||||
|
|
Σ |
|
|
|
|
Σ |
2 |
|
Σ |
3 |
|
|
|
|
|
|
|
|
|
k =1 |
|
1 |
|
|
|
|
|
|
|
k |
|
|
|
|
Σ |
|
||||
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||
так как интегралы по Σ(k ) равны нулю, а по поверхности Σ(k ) |
и Σ(k ) составля- |
|||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
ют в сумме интеграл по поверхности Σ(k ) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Часть 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично для Hx и Hy областей справедливо: |
|
|
||||||||||||||||||
∫∫∫ |
∂ay |
dxdydz = |
∫∫ay cos βdσ ; ∫∫∫ |
|
∂a |
x |
dxdydz = ∫∫ax cosαdσ . |
|||||||||||||
∂y |
|
|
|
|
|
|
|
|
||||||||||||
G |
|
|
|
Σ |
|
|
G |
|
∂x |
|
Σ |
|
||||||||
Складывая почленно, получаем утверждение теоремы.
!1). Координатная форма записи теоремы Остроградского-Гаусса имеет вид:
∫∫(ax cosα + ay cos β + az cosγ )dσ = = ∫∫∫( |
∂a |
x + |
∂ay |
+ |
∂a |
z )dxdydz , |
|
|
∂y |
|
|||||
Σ |
G |
∂x |
|
∂z |
|||
где cosα,cos β,cosγ - координаты единичного вектора внешней норма-
ли.
2). Используя обозначение дивергенции, формулу ОстроградскогоГаусса можно записать в виде:
∫∫(a n0 )dσ =∫∫∫diva dxdydz = ∫∫∫( a)dxdydz .
Σ |
G |
G |
Поток векторного поля (вектора) через внешнюю сторону замкнутой поверхности Σ равен тройному интегралу от diva по пространственной области G, ограниченной поверхностью Σ.
Применение теоремы Остроградского - Гаусса
Пример:
Вычисление объемов.
Пусть a(x, y, z) = r ; r = (x, y, z) ; div(a) = div(r ) =1+1+1 = 3 .
∫∫∫3dxdydz = ∫∫x cosαdσ + y cos βdσ + z cosγdσ ,
G |
|
|
Σ |
V |
= |
1 |
∫∫(xdydz + ydxdz + zdxdy) . |
|
|
3 |
Σ |
Теория поля |
57 |
Пример:
Вычисление потоков.
Вычислить поток поля a = x2 i + y 2 j + z 2 k через замкнутую поверхность
Σ: x |
|
+ y |
|
+ z |
|
= |
R |
|
, . |
|
|
|
|
||
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
z = 0 |
(z ≥ 0). |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|||
Решение: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Π = ∫∫(a,dσ) = ∫∫∫divadxdydz = |
|
|
|
|
|||||||||||
|
0 |
||||||||||||||
|
|
Σ |
|
|
|
|
|
|
G |
|
|
|
|
||
∫∫∫(2x + 2 y + 2z)dxdydz =… |
|
|
|
|
|||||||||||
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
{перейдём в сферическую систему коорди- |
|
|
|
||||||||||||
X |
xy |
||||||||||||||
нат} |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
…= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2∫π |
π |
|
|
|
|
|
|
|
|
|
|
πR4 . |
|||
dϕ ∫2 sinθdθ∫R r2dr(2r cosϕ sinθ + 2r sinϕ sinθ + 2r cosθ) = |
|||||||||||||||
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
Пример:
Найти поток поля a = x2 i + y 2 j + z 2 k через внешнюю сторону полусфе-
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
ры: Σ: x |
|
+ y |
|
+ z |
|
= R |
|
, |
|
|
|
|
|
|
|
|
|
|
|
||
z ≥ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся |
результатами |
предыдущей |
|
|
|
|
|
|
|||||||||||||
|
1 |
0 |
1 |
||||||||||||||||||
задачи. Замкнем поверхность |
Σ1 поверхно- |
|
|
|
|
|
Y |
||||||||||||||
стью Σ2 , |
которая представляет собой часть |
xy |
|
|
|
||||||||||||||||
X |
|
2 2 |
|
||||||||||||||||||
плоскости XOY. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П = П1 + П2 = πR4 |
, П1 = П − П2 , Π2 = ∫∫(a, n0 )dσ = |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Σ2 |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
} |
|
) |
|
|
|
|
|
|||||
=…{ (a n |
|
) = |
|
x2 ; y2 ; z2 |
|
{0;0;−1} = −z2 }… = − |
|
z2dσ = 0, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Σ2 |
|
|
|
|
т.к. на Σ2 z = 0 и П1 = П − П2 |
= |
πR4 |
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
7.8. Инвариантное определение дивергенции
Пусть a = a(P) - векторное поле, удовлетворяющее условию теоремы Остроградского – Гаусса. Пусть точка M - произвольная точка области G.
