2. Далее рассмотрим, как выглядит эпюра изгибающих моментов в консольной балке при приложенном на ее свободном конце сосредоточенном моменте m ( рис.19 ).

Рис.19

Проведем сквозное сечение 1-1 через точку k и рассмотрим равновесие отсеченной части балки (которая, как-бы, «висит» в воздухе). Запишем выражение для суммы моментов всех внешних и внутренних сил, действующих на отсеченный участок, относительно точки k.

Так как выбор точки для проведенного сечения был произвольным, делаем вывод о постоянстве величины искомого изгибающего момента по всей длине балки. Очертание изогнутой оси консольной балки при данном силовом воздействии приведено на рис.20. Из анализа рисунка следует, что и в данном случае растянутыми являются верхние волокна, а посему эпюра М будет расположена также сверху от нейтральной оси балки ( рис.21 ).

- 12 -

3. «Загрузим» консольную балку равномерно-распределенной нагрузкой q (рис.22). Заметим, что под ее интенсивностью q понимается нагрузка, приходящаяся на единицу длины балки. 1

Проведем сквозное сечение 1-1 через точку k и рассмотрим равновесие отсеченной части балки (которая, как-бы, «висит» в воздухе). Заменим равномерно-распределенную нагрузку на участке длиной x ее равнодействующей R=q×x (рис.23,а) и вычислим момент этой равнодействующей относительно точки k: x/2)= qx²/2. Из курса аналитической геометрии известно, что уравнение квадратной параболы, проходящей через начало координат, выглядит аналогично: Следовательно, эпюра моментов в нашем случае очерчена по квадратной параболе с двумя характерными точками: при x=0 - М=0, а при x=L – M=qL²/2. Очертание изогнутой оси консольной балки при данном силовом воздействии приведено на рис.23,б. Из анализа рисунка следует, что в данном случае растянутыми являются верхние волокна, из-за чего эпюра М должна быть расположена сверху от нейтральной оси балки.

При построении данной криволинейной эпюры дополнительно надо определить ее характер, т.е. «выпуклая» она или же «вогнутая». На этот вопрос легко ответить, применив т.н. «правило паруса». Оно базируется на простой аналогии с вогнутостью реального паруса под действием ветра:

Итак, при действии равномерно-распределенной нагрузки эпюра моментов очерчена по квадратной параболе с выпуклостью, совпадающей с направлением действия этой нагрузки .

На рис.24 изображена эпюра изгибающих моментов при действии равномерно-распределенной нагрузки на консольную балку.

- 13 -

qL²/2

На базе трех полученных выше «табличных» случаев продолжим расчет консольных балок на действие различных сочетаний нагрузок для приобретения элементарных практических навыков в построении эпюр изгибающих моментов.

Пример 1.

Анализ предложенной задачи приводит к следующим выводам:

- данная конструкция является консольной балкой;

- определение опорных реакций в такой конструкции необязательно;

- построение эпюры моментов следует начинать со свободного конца;

- число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков для лучшего усвоения предлагаемого алгоритма построения эпюры изгибающих моментов. Расчет начинаем с участка 1-2. Для этого прибегнем к такому приему – мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис.25,а). При этом участок 1-2 становится аналогом первого частного случая (см. рис.18), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис.25,б).

• 14 –

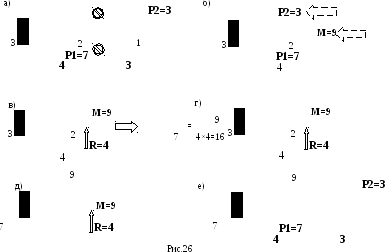
На следующем шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис26,а). При этом балка в сечении 2 восстанавливает свои кинематические характеристики. Далее рассмотрим участок 2-3. Приложим к нему сосредоточенный момент М=9, отложенный выше нейтральной оси в сечении, правее т.2 (см. рис.25,б) и растягивающий, таким образом, верхние волокна. Кроме того, на участок 2-3 переносим сосредоточенную силу Р₂=3, прикладываем ее в точке 2 (рис.26,б) и добавляем сосредоточенную силу Р₁= 7. Определим равнодействующую двух вертикальных сил в сечении 2: R = P₁-P₂= 7-3= 4 (рис.26,в). Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=9 соответствует частному случаю 2 (рис.21), приводя к растяжению верхних волокон. Отложим ординату 9 выше нейтральной оси (рис.26,г); независимое действие сосредоточенной силы R=4 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна М₃=Р×L=4×4=16. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16-9=7. Этот момент растягивает нижние волокна. В пределах характерного участка 2-3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2-3 – на рис.26,д. На рис. 26,е изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой сосредоточенных сил.

- 15 –

Обратим внимание на характерную особенность полученной эпюры в сечении 2. При действии сосредоточенной силы на эпюре изгибающих моментов в этом сечении наблюдается перелом (или же излом) в сторону действия этой нагрузки. Это свойство широко применяется при визуальном контроле правильности построения эпюры изгибающих моментов.