
- •Статистика
- •II. Содержание дисциплины
- •III. Краткие сведения из теории
- •3.1. Предмет и методы статистики
- •3.2. Статистическое наблюдение
- •3.3. Статистическая сводка и группировка.
- •4.4. Абсолютные статистические величины
- •4.5. Средние величины
- •Средняя арифметическая.
- •Средняя гармоническая
- •Средняя геометрическая
- •Структурные средние
- •4.6. Изучение вариации признака в совокупности
- •Правило сложения дисперсий
- •4.6. Выборочное наблюдение
- •4.6. Статистическое изучение рядов динамики
- •4.7. Индексные метод в статистике
- •1) Физического объема:
- •2) Цен:
- •4.8. Статистическое изучение взаимосвязей
- •Количественные критерии оценки тесноты связи
- •Оценка линейного коэффициента корреляции
- •III. Задание к контрольной работе Задание 1
- •Задание 2
- •Задание 3
- •Задание 4.
- •V. Материалы для практических занятий
- •5.1. Стаистическое наблюдение
- •5.2. Сводка и группировка статистических данных.
- •5.3. Статистические показатели
- •5.4. Распределение признака в совокупности
- •5.5. Выборочные наблюдения.
- •5.6. Ряды динамики
- •5.6. Индексы
- •Статистическое изучение взаимосвязей.
- •VI. Рекомендуемая литература.
- •Итоги деятельности предприятий промышленности региона за год
- •Исходный данные для решения задачи 3
3.3. Статистическая сводка и группировка.
Важнейшим этапом исследования социально-экономических явлений и процессов является систематизация первичных данных и получение на этой основе сводной характеристики объекта в целом при помощи обобщающих показателей, что достигается путем сводки и группировки первичного статистического материала.
Статистическая сводка - это комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.
По глубине и точности обработки материала различают сводку простую и сложную.
Простая сводка - это операция по подсчету общих итогов по совокупности единиц наблюдения.
Сложная сводка - это комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц.
Проведение сводки необходимо осуществлять по следующим этапам:
• выбор группировочного признака;
• определение порядка формирования групп;
• разработка системы статистических показателей для характеристики групп и объекта в целом;
• разработка макетов статистических таблиц для представления результатов сводки.
Статистической группировкой называется расчленение единиц изучаемой совокупности на однородные группы по определенным, существенным для них признакам.
В соответствии с задачами группировки различают следующие ее виды: типологическая, структурная, аналитическая.
Типологическая группировка - это расчленение разнородной совокупности на отдельные качественно однородные группы и выявление на этой основе экономических типов явлений.
группировки должно осуществляться на основе анализа сущности изучаемого явления.
Структурной называется группировка, которая предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку.
Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой.
В статистике признаки можно разделить на факторные и результативные. Факторными называются признаки, оказывающие влияние на изменение результативных. Результативными называются признаки, изменяющиеся под влиянием факторных. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает значение признака результативного.
Все рассмотренные группировки могут быть построены по какому-то одному или нескольким существенным признакам.
Группировка, в которой группы образованы по одному признаку, называется простой.
Сложной называется группировка, в которой расчленение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации). Сначала группы формируются по одному признаку, затем эти группы делятся на подгруппы по другому признаку, которые, в свою очередь, делятся по третьему признаку, и т. д. Итак, сложные группировки дают возможность изучить единицы совокупности одновременно по нескольким признакам.
При построении сложной группировки возникает вопрос о последовательности разбиения единиц объекта по видам признаков. Как правило, рекомендуется сначала производить группировку по атрибутивным признакам, значения которых имеют ярко выраженные качественные различия, а затем - по количественным.
Построение группировки начинается с определения состава группировочных признаков.
Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования.
В основание группировки могут быть положены как количественные, так и атрибутивные признаки. Первые имеют числовое выражение (объем торгов, возраст человека, доход семьи и т. д.), а вторые отражают состояние единицы совокупности (пол человека, семейное положение, отраслевую принадлежность предприятия, его форму собственности и т. д.).
После того как определено основание группировки, следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность.
Если группировка строится по атрибутивному признаку, то групп, как правило, будет столько, сколько имеется градаций, видов состояний у этого признака. Например, группировка предприятий по формам собственности учитывает муниципальную, федеральную и собственность субъектов Федерации.
Определение числа групп можно осуществить и математическим путем с использованием формулы Стерджесса:
![]() (1)
(1)
где n - число групп;
N - число единиц совокупности.
Когда определено число групп, то следует определить интервалы группировки.
Интервал - это значение варьирующего признака, лежащее в определенных границах.
Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки в зависимости от их величины бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.
Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами.
Величина равного интервала определяется по следующей формуле:
![]() (2)
(2)
где хмах и xmin - максимальное и минимальное значения признака в совокупности;
n - число групп.
Округление величины интервала может проводится только в большую сторону.
Если размах вариации признака совокупности велик и значения признака варьируются неравномерно, то необходимо использовать группировку с неравными интервалами.
Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница несущественна.
Интервалы группировок могут быть закрытыми и открытыми.
Закрытыми называются интервалы, у которых имеются верхняя и нижняя границы. У открытых интервалов указана только одна граница: верхняя - у первого, нижняя - у последнего.
При группировке единиц совокупности по количественному признаку границы интервалов могут быть обозначены по-разному в зависимости от того, непрерывный это признак или прерывный.
Если основанием группировки служит непрерывный признак, то может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов. Для того чтобы правильно отнести к той или иной группе единицу объекта, значение признака у которой совпадает с границами интервалов, можно использовать открытые интервалы. Решение об открытии нижней или верхней границы может быть принято самостоятельно.
Если в основании группировки лежит прерывный признак, то нижняя граница 1-го интервала равна верхней границе (i-1) интервала, увеличенной на 1. Например, группы строительных фирм по числу занятого персонала будут иметь вид (чел.): 100 - 150, 151 -200, 201 -300.
При наличии достаточно большого количества вариантов значений признака первичный ряд является трудно обозримым, и непосредственное рассмотрение его не дает представления о распределении единиц по значению признака в совокупности. Поэтому первым шагом в упорядочении первичного ряда является его ранжирование, т. е. расположение всех вариантов в возрастающем (или убывающем) порядке.
Например, стаж работы (годы) 22 рабочих бригады характеризуется следующими данными: 2, 4, 5, 5, 6, 6, 5, 6, 6, 7, 7, 8, 8, 9, 10, 11, 4, 3, 3, 4, 4, 5.
Ранжированный ряд, построенный по этим данным: 2, 3, 3, 4. 4, 4. 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 8, 8, 9, 10, 11.
При рассмотрении первичных данных можно
видеть, что одинаковые варианты признака
у отдельных единиц повторяются (здесь
и далее
![]() - частота повторения;
- частота повторения;![]() - объем изучаемой совокупности).
- объем изучаемой совокупности).
Способы построения дискретных и интервальных рядов различны.
Для построения дискретного рядас
небольшим числом вариантов выписываются
все встречающиеся варианты значений
признака![]() ,
а затем подсчитывается частота повторения
варианта
,
а затем подсчитывается частота повторения
варианта![]() ,.
Ряд распределения принято оформлять в
виде таблицы, состоящей из двух колонок
(или строк), в одной из которых представлены
варианты, в другой - частоты. Построение
дискретного вариационного ряда не
составляет труда.
,.
Ряд распределения принято оформлять в
виде таблицы, состоящей из двух колонок
(или строк), в одной из которых представлены
варианты, в другой - частоты. Построение
дискретного вариационного ряда не
составляет труда.
Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов (<от-до>), необходимо установить оптимальное число групп (интервалов), на которое следует разбить все единицы изучаемой совокупности. При группировке внутри однокачественной совокупности появляется возможность применения равных интервалов, число которых зависит от вариации признака в совокупности и от количества обследованных единиц.
Проиллюстрируем построение интервального вариационного ряда по данным приведенного ранее примера распределения рабочих по стажу работы.
Для нашего примера, согласно формуле
Стерджесса (3.1), при
![]() число групп
число групп![]() .
Зная число групп, определим интервал
по формуле (2):
.
Зная число групп, определим интервал
по формуле (2):
![]() .
.
В результате
получим следующий ряд распределения
рабочих по стажу работы (![]() ):
):
![]() ... 2-4 4-6 6-8 8-10 10-12
... 2-4 4-6 6-8 8-10 10-12
![]() …
3 8 6 3 2
…
3 8 6 3 2
Как видно из данного распределения, основная масса рабочих имеет стаж работы от 4 до 8 лет.
От группировок следует отличать классификацию. Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.
Отличительной чертой классификации является то, что в основу ее кладется атрибутивный признак. Классификации стандартны, устойчивы, т. е. остаются неизменными в течение длительного периода времени, и, как правило, разрабатываются органами государственной и международной статистики.
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.
Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями и получают ломанную линию, называемую полигоном частот. Для замыкания полигона крайние точки (слева и справа на ломанной линии) соединяют с точками на оси абсцисс и получают многоугольник. По данным табл. 1 построим полигон (рис. 1).
Таблица 1
Распределение работников строительной фирмы «Скат»
по уровню дохода в январе 1998 г.
|
Группы работников, по уровню дохода, руб. |
Число работников, Чел. |
Удельный вес, % к итогу |
|
До 5 000 |
60 |
52,2 |
|
5 000 - 7 500 |
30 |
26,1 |
|
7 500 - 10 000 |
15 |
13,0 |
|
10 000 и более |
10 |
8,7 |
|
Итого |
115 |
100,0 |
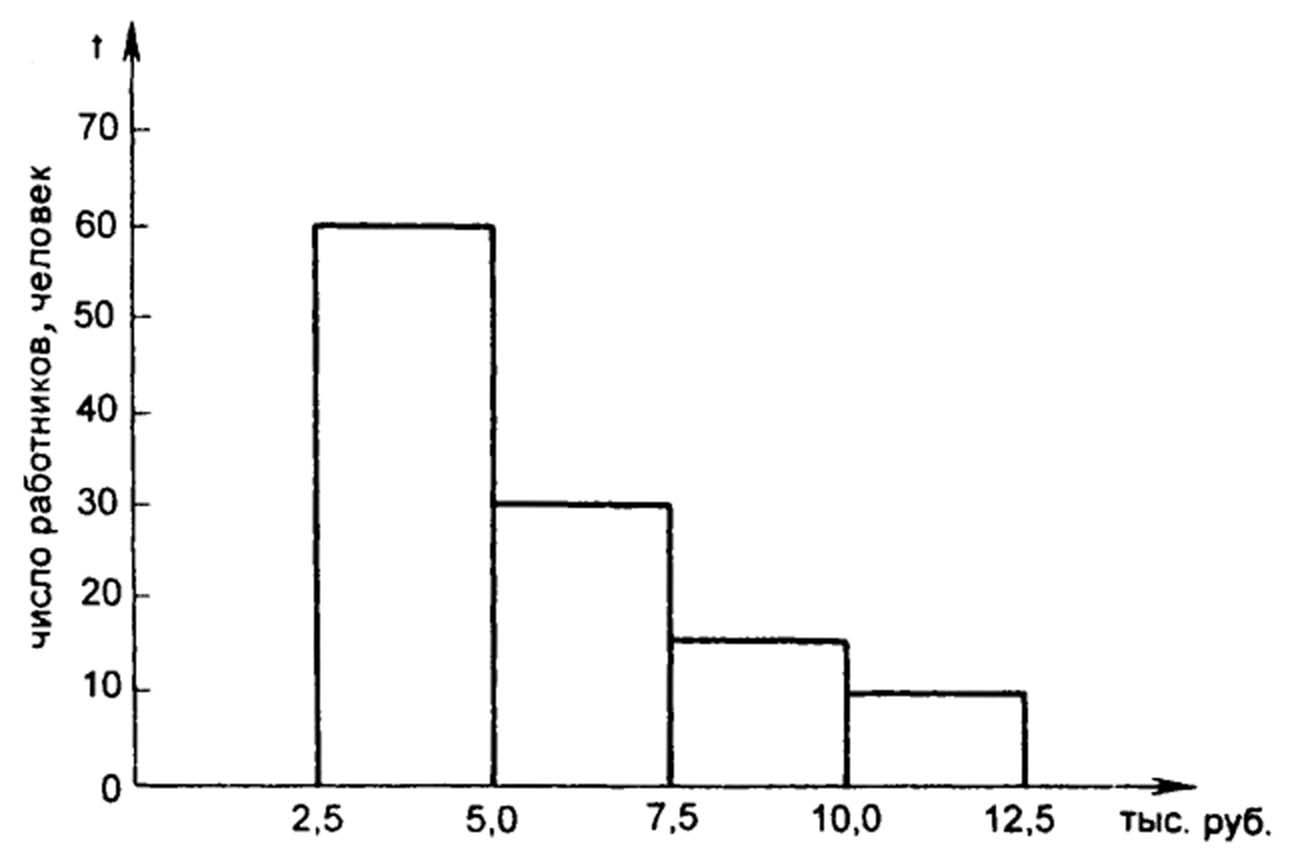
Рис.1. Полигон распределения работников строительной фирмы "Скат"
по уровню дохода в январе 1998 г.
Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получим гистограмму-график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.
Если середины верхних сторон прямоугольников соединить прямыми, то гистограмма может быть преобразована в полигон распределения (рис. 2).

Рис. 3.2. Гистограмма и полигон распределения работников строительной фирмы «Скат» по уровню дохода в январе 1998 г.
Для графического изображения вариационных рядов может использоваться также кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака, не большие, чем рассматриваемое значение.
При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат - накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломанную линию, т.е. кумуляту. Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву.
