
- •Статистика
- •II. Содержание дисциплины
- •III. Краткие сведения из теории
- •3.1. Предмет и методы статистики
- •3.2. Статистическое наблюдение
- •3.3. Статистическая сводка и группировка.
- •4.4. Абсолютные статистические величины
- •4.5. Средние величины
- •Средняя арифметическая.
- •Средняя гармоническая
- •Средняя геометрическая
- •Структурные средние
- •4.6. Изучение вариации признака в совокупности
- •Правило сложения дисперсий
- •4.6. Выборочное наблюдение
- •4.6. Статистическое изучение рядов динамики
- •4.7. Индексные метод в статистике
- •1) Физического объема:
- •2) Цен:
- •4.8. Статистическое изучение взаимосвязей
- •Количественные критерии оценки тесноты связи
- •Оценка линейного коэффициента корреляции
- •III. Задание к контрольной работе Задание 1
- •Задание 2
- •Задание 3
- •Задание 4.
- •V. Материалы для практических занятий
- •5.1. Стаистическое наблюдение
- •5.2. Сводка и группировка статистических данных.
- •5.3. Статистические показатели
- •5.4. Распределение признака в совокупности
- •5.5. Выборочные наблюдения.
- •5.6. Ряды динамики
- •5.6. Индексы
- •Статистическое изучение взаимосвязей.
- •VI. Рекомендуемая литература.
- •Итоги деятельности предприятий промышленности региона за год
- •Исходный данные для решения задачи 3
Средняя гармоническая
Средняя арифметическая, как было показано
выше, применяется в тех случаях, когда
известны варианты варьирующего признака
![]() и их частоты
и их частоты![]() .
.
Когда статистическая информация не
содержит частот
![]() по отдельным вариантам
по отдельным вариантам![]() совокупности, а представлена как их
произведение
совокупности, а представлена как их
произведение![]() ,
применяется формуласредней гармонической
взвешенной. Чтобы исчислить среднюю,
обозначим
,
применяется формуласредней гармонической
взвешенной. Чтобы исчислить среднюю,
обозначим![]() ,
откуда
,
откуда![]() .
Теперь преобразуем формулу средней
арифметической таким образом, чтобы по
имеющимся Данным
.
Теперь преобразуем формулу средней
арифметической таким образом, чтобы по
имеющимся Данным![]() и
и![]() можно было исчислить среднюю. В формулу
средней арифметической взвешенной
(5.4) вместо
можно было исчислить среднюю. В формулу
средней арифметической взвешенной
(5.4) вместо![]() подставим
подставим![]() ,
вместо
,
вместо![]() - отношение
- отношение![]() и получим формулусредней гармонической
взвешенной.
и получим формулусредней гармонической
взвешенной.
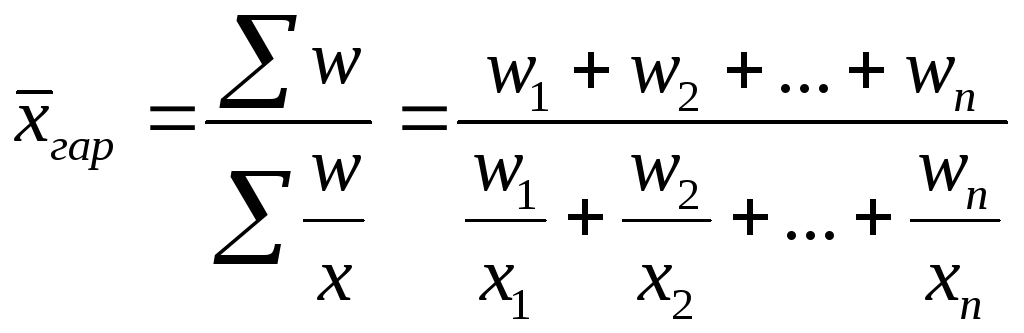 . (5.9)
. (5.9)
Из формулы (5.9) видно, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужна определить веса отдельных значений признака, скрытые в весах средней гармонической.
Например, по данным (табл. 5.5) требуется определить среднюю цену 1 кг картофеля.
Таблица 5.5
Цена и выручка от реализации по трем коммерческим магазинам в октябре 1996 г.
|
Номер магазина |
Цена картофеля, руб/кг,
|
Выручка от реализации, млн. руб.,
|
Частота (количество реализованных едениц), кг,
|
|
1-й 2-й 3-й |
800 1000 900 |
24 15 18 |
30000 15000 20000 |
|
Итого |
- |
57 |
65000 |
Расчет средней цены выражается соотношением:
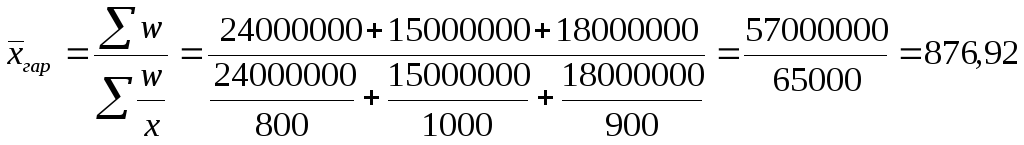 .
.
В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:
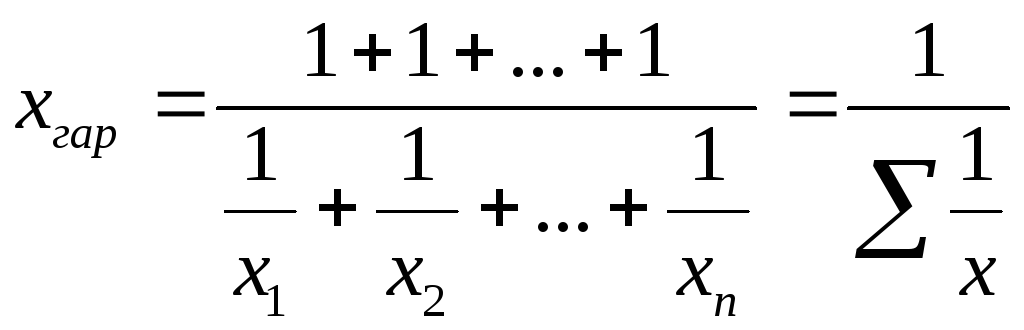 , (5.10)
, (5.10)
где
![]() - отдельные варианты обратного признака,
встречающиеся по одному разу;
- отдельные варианты обратного признака,
встречающиеся по одному разу;![]() - число вариантов.
- число вариантов.
Средняя геометрическая
Применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическаяисчисляется
извлечением корня степени![]() из произведений отдельных значений -
вариантов признака
из произведений отдельных значений -
вариантов признака![]() :
:
![]() ,
,
где
![]() - число вариантов;П- знак произведения.
- число вариантов;П- знак произведения.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Структурные средние
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода![]() - значение случайной величины,
встречающееся с наибольшей вероятностью,
в дискретном вариационном ряду - вариант,
имеющий наибольшую частоту.
- значение случайной величины,
встречающееся с наибольшей вероятностью,
в дискретном вариационном ряду - вариант,
имеющий наибольшую частоту.
В интервальных рядах распределения с равными интервалами модавычисляется по формуле:
 , (5.16)
, (5.16)
где
![]() - нижняя граница модального интервала;
- нижняя граница модального интервала;![]() - модальный интервал;
- модальный интервал;![]() ,
,![]() ,
,![]() - частоты в модальном, предыдущем и
следующем за модальным интервалах
(соответственно).
- частоты в модальном, предыдущем и
следующем за модальным интервалах
(соответственно).
Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.
Медиана![]() - это вариант, который находится в
середине вариационного ряда. Медиана
делит ряд на две равные (по числу единиц)
части – со значениями признака меньше
медианы и со значениями признака больше
медианы. Чтобы найти медиану необходимо
отыскать значение признака, которое
находится в середине упорядоченного
ряда. В ранжированных рядах несгруппированных
данных нахождение медианы сводится к
отысканию порядкового номера медианы.
- это вариант, который находится в
середине вариационного ряда. Медиана
делит ряд на две равные (по числу единиц)
части – со значениями признака меньше
медианы и со значениями признака больше
медианы. Чтобы найти медиану необходимо
отыскать значение признака, которое
находится в середине упорядоченного
ряда. В ранжированных рядах несгруппированных
данных нахождение медианы сводится к
отысканию порядкового номера медианы.
Пусть ряд состоит из показателей заработной платы 9 рабочих, тыс. руб. в месяц (в 1996 г.):
630, 650, 680, 690, 700, 710, 720, 730, 750.
Номер медианы для нечетного объема вычисляется по формуле:
![]() ,
,
где
![]() - число членов ряда.
- число членов ряда.
В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
В интервальных рядах распределения
медианное значение (поскольку оно делит
всю совокупность на две равные по
численности части) оказывается в каком-то
из интервалов признака
![]() .
Этот интервал характерен тем, что его
кумулятивная частота (накопленная сумма
частот) равна или превышает полусумму
всех частот ряда. Значениемедианывычисляется линейной интерполяцией по
формуле:
.
Этот интервал характерен тем, что его
кумулятивная частота (накопленная сумма
частот) равна или превышает полусумму
всех частот ряда. Значениемедианывычисляется линейной интерполяцией по
формуле:
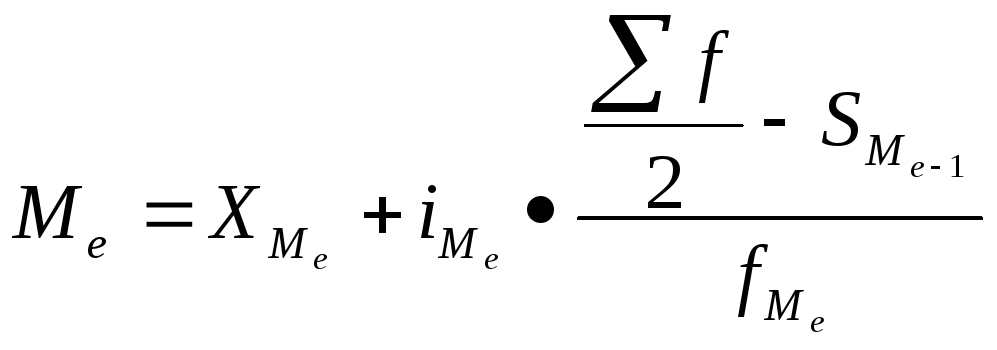 , (5.17)
, (5.17)
где
![]() - нижняя граница медианного интервала;
- нижняя граница медианного интервала;![]() - медианный интервал;
- медианный интервал;![]() - половина от общего числа наблюдений;
- половина от общего числа наблюдений;![]() - сумма наблюдений, накопленная до начала
медианного интервала,
- сумма наблюдений, накопленная до начала
медианного интервала,![]() - число наблюдений в медианном
интервале.
- число наблюдений в медианном
интервале.
Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.
