bekbaev_energetikadagy_umk_kz_2012

dV

=

¶V

X

1

+

¶V

X

2

+ ... +

¶V

X

n

,

dt

¶x

¶x

2

¶x

n

1

мұнда X1, X 2 ,..., X n - өзiмен x1, x2 ,..., xn ауытқуларынан									таңдалған функцияларды
ұсынатын теңдеулердiң оң бөлiктерi (8.1).
Демек, Ляпунов функциясынан туынды əр уақытта,сонымен қатар өзі
сияқты ауытқулардың кейбiр функциясы болып табылады, яғни
				dV	=W (x , x ,..., x ),					(8.4)
				dt		1	2	n
жəне де	өз	қасиетіне(8.2)		сəйкес			бұл W функциясы дəл V сияқты
x1 = x2 = ... = xn	= 0	болғанда нөлге айналады.
Сондықтан оған бiрдей			дəрежеде				тұрақтылық жəне жоғары			айтылатын
V функциясына қатысты түсініктерді қолдануға болады.
Бұл жерде мəселе тек теңдеулер							туралы ғана болады, оларға t уақыт
нақты түрде кірмейді. Жалпы Ляпунов əдісі t уақыт нақты түрде болғанда да
қолданылуы мүмкін, негізінен ауыспалы коэффиценттері бар теңдеулер үшін.
Осы	мəліметтерге		сүйене				отырып		сызықтық	емес	жүйелер

тұрақтылығы мен тұрақсыздығы туралы Ляпунов теоремасының жалпы түсініктемесін береміз. Егер берілген реттеу жүйесінің бастапқы теңдеулері дұрыс болса бұл теоремалар реттеу жүйелерін үлкен жəне кіші ауытқулар кезінде де зерттеуге пайдаланылады. Кез - келген үлкен ауытқу кезінде жүйенің тұрақтылығы қысқаша жалпы тұрақтылық деп аталады.

Сызықтық емес жүйелердің тұрақтылығы туралы Ляпунов теоремасы.

Теорема келесі түрде құрылады: егер п қатарындағы теңдеу жүйесі формасында

берілген, уақыт бойынша туындысыW (x1 , x2 ,..., xn )нақты болатын,

бірақ V

белгісіне

карсы W (x1 , x2 ,..., xn )

туындысы

болса ол жүйе тұрақты деп

есептеледі.W нақты функциясы кезінде

асимптотикалық

тұрақтылық

пайда болады.

Осы

теореманың

дұрыстығын

геомтриялық

мысалдар

сипаттайық. Жеңілдік үшін үшінші ретті жүйені алайық(п = 3). Ол үшін

(8.1) теңдеудің жалпы түрі мынандай болады:

dx1

= X

(x

, x

, x

),

ü

1

ï

dt

1

2

3

ï

dx 2

= X

2 (x1 , x2 , x3 ),ýï

(8.5)

dt

ï

dx3

= X

(x

, x

, x

).

ï

3

ï

dt

1

2

3

þ

Ляпуновтың тұрақты оң функциясын аламыз

31

V = a 2 x 2	+ b2 x 2		+ c 2 x 2		(8.6)
1		2		3
мұнда а, b, с – кез-келген нақты		сандар.		V мəніне V=0, C1 , C 2 , C3 , ....,	өспелі

нақты мəндерді береміз, бұл мынаны білдіреді.

		a2 x2	+ b2 x2	+ c2 x2	= 0
		1	2	3
		a2 x2	+ b2 x2	+ c2 x = C		,
		1	2		1
		a2 x2	+ b2 x2	+ c2 x2	=C	2	,
		1	2	3
		..........	..........	..................			·
Бұл	өрнектің	біріншісі		ғанаx = x		2	= x	3	= 0	нүктесіне	сай, ал
				1

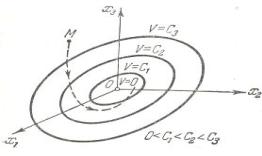
қалғандары фазалық кеңістіктегі элипсоидтардың бетіне сай болады. Əр алдыңғы элипсоид келесі элипсоидтың(8.2 сурет) ішінде орналасады. Енді уақыт бойынша Ляпунов функциясынан туынды аламыз. (8.3) жəне

(8.4) сəйкес

dV

= 2a 2 x X

1

(x , x

, x

)+ 2b2 x

2

X

2

(x , x

, x

)+ 2c 2 x

X

(x , x

, x

)= W (x , x

, x

),

3

dt

1

1

2

3

1

2

3

3

1

2

3

1

2

3

мұнда

X 1 , X 2 , X 3

функциялары

реттеу

жүйесінің(8.5)

берілген теңдеулерінен

алынады.

Егер осындай жолмен алынғанW(x1, x2, xs) функциясы теріс нақты, т.б

егер

dV

p 0

(8.7)

dV

dt

болса

= 0

( x

= x

2

= x

3

= 0

бойынша)

координаттар

басынан басқа

1

dt

зерттелетін фазалық кеңістіктің барлық нүктелеріндеМ нүктесі F азаю жағына қарай жылжиды, яғни элипсоидтарды қиып өтеді (8.2-сурет).

8.2 - сурет. Фазалық кеңістік

Нəтижесінде уақыт ағымымен М бейнелеуші нүктесіО фазалық кеңістігінің координаттар басына ұмтылады жəне өзі кірген элипсоидтардың сыртына шыға алмайды.

32

y = F(x)

		Бұл	уақыт		ағымы	бар	өтпелі	процесстерде x ,		xбарлық, x
									1	2	3
ауытқулардың сөнетінін білдіреді. Осылайша осы реттеу жүйесінің
тұрақтылығы анықталады. Бұл теореманың үшінші рет									үшін		дұрыс
екенін көрсетеді.
		Осыдан теореманың жалпы жағдайда да дұрыс болатыны көрінеді.
Пікірлер			сол күйде қалады, тек үш теңдеу					орнынаn	теңдеулер
қолданылады. Бұрынғыдай Ляпуновтың барлық V (x1 , x2 ,..., xn ) = C нақты оң
функциясы			үшін бірқатар тұйық кеңістіктерді аламыз, бірақ олар							енді
үш		өлшемді			фазалық кеңістіктерде			болады.	Сондықтан
	dV	= W (x , x	,..., x	) туындысы нақты теріс болса n кеңістігіндегі М бейнелеуші
	dt	1 2	n
нүктесінің			траекториясы			кез-келген	бастапқы	шарттарда		көерсетілген

кеңістіктерді ішінен сыртына қарай қиып өтеді. Бұл жүйенің тұрақты екенін көрсетеді.

Негізгі əдебиеттер: 3 [324-348]. Қосымша əдебиеттер: 1 [365-414]. Бақылау сұрақтар:

Орнықтылық жəне сызықты емес жүйелердiң сапасының кейбiр бағалары. Ляпуновтың функциясы жəне оның уақыт бойынша туындысы.

Сызықты емес жүйелердiң орнықтылығы туралы Ляпуновтың теоремасы. V функция қашан нақтылы деп аталады?

V функция қашан қарсы таңбалы деп аталады? V функция қашан тұрақты таңбалы деп аталады?

Дəрістің тақырыбы: 9 Сызықты емес жүйелердiң абсолюттi

орнықтылық шарттары. В. М. Попов критериясы.

Дəріс конспектісі. Құрылымдық сұлбасы 9.1- суретте көрсетілгендей түрге келтiруге болған сызықты емес жүйелерді қараймыз. Бұл сұлбада

сипаттамасы бар инерциясыз сызықты	емес	элемент	жəkне(t) өтпелі
			И
инерциялы, нөлге тең статикалық беру	коэффиценті барW (s) берілісті
функциялы сызықты бөлік бар. Барлық əсерлер бір		кіріске	келтірілген жəне
f (t ) түрінде белгіленген.

9.1- сурет. Сызықты емес жүйелердiң құрылымы

33

(9.1)

(9.2)

суреттеу

Жүйенің дифференциалды теңдеуінің шешімінF(s) əсерді жəне Y (s) = L{F[x(t)]} координаттары арқылы бейнелейміз:

X (s) = F (s) -W (s)L{F[x(t)]}

Түпнұсқаға өте отырып екінші ретті Вольтер интегралды теңдеуін аламыз:

t

x(t) = f (t) - z(t) = f (t) - òk И (t -t )F[x(t )]dt .

			0
Жүйені	модуль	бойынша	шектелген		жəне	уақыттың			жоғалаты
функциясы	болып	табылатын	əсерлер	кезінде		қарастырамыз. sup		f (t )

(supremum) максималды əсерін белгілейміз.

f (t ) уақыттың жоғалу функциясы деп уақыт ағымымен нөлге ұмтылатын функцияны атаймыз:

lim f (t )= 0 .

t ®¥

Егер əсер болмаса 9.1-ден мынау шығады

t
x(t )= -òk И (t -t )F[x(t )]dt .	(9.3)
0

Егер сызықтық емес сипаттама координаттар басымен өтсе, яғни Ф(0)=0 болса (9.3) теңдеуінің тепе-теңдік жағдайына сай тривиалды шешімі болады

							x(t) º 0,	(9.4)
Егер l(A)f 0 болғанда оң мəні болса
	sup				f (t )		= l(A)	(9.5)
т е ң с і з д і г і о р ы н а л а д ы .
	x(t)		£ A,					(9.6)

м ұ н д а А - к а н д а й д а б о л м а с ы н а з о ң м ə н .

Осыған сəйкес, l(A)-ның қандай мағынасында (9.5) жəне (9.6) теңдеулері орындалатынын, орнықтылқтың үш түрін айқынтаймыз: аз орнықтылық егер l(A)-шексіз кішкентай, үлкен орнықтылық егер sup f (t ) - соңғы орнықтылық, жəне бүтін орнықтылық, егер sup f (t ) шексіз.

Қандай болмасын нақтылы сыныпқа тəуелдi Ф(х) сипаттамасына орын бар тепе-теңдiк жағдайының орнықтылығын негiзiнен абсолюттi орнықтылық деп атайды.

34

r

болып

Ф (х) сыныбының сипаттамасы үшін жақсы игерiлген əдiс болып екi тура сəулелердiң арасындағы, бiрiншi координаталар басы арқылы өтетiн жəне жəне K бұрыштық коэффиценттері бар орнықтылықтар зерттеулері табылады.

( r , K ) секторына тиісті жəне осышектеулерді қанағаттандыратын сипаттамаларын, сипаттамасы дап атайтын боламыз.

В. М. Поповоның жиiлiк əдiсi

Енді румын ғалымы В. М. Попов ұсынған қолдануында берілген есептер əлдеқайда оңай мысалдармен шешілетін бөлшектік əдісті назарларыңызға ұсынамыз.

Егер автоматты реттеу жүйесінде тек қана жалғыз бiрмəндi сызықты емес

болса

y = F (x) ,

(9.7)

онда жүйенiң (сызықты) барлық өзге теңдеулерiн бiрге топтастырып,

9.2 - сурет. ( а ) сызықты емес жүйе жəне y = F (x1 ) (б)

əрдайым жүйенiң сызықтық бөлiгiнің келесі түрдегi ортақ теңдеуін (9.2- а сурет) алуға болады

Q( p)x = -R( p) y ,										(9.8)
мұнда				p n + a p n-1						,
Q( p)x = a		0			+ ... + a		n-1	p + a	n
				1						,
R( p)x = b	0		p m + b p m-1		+ ... + b	m-1		p + a	m
				1

т < п деп санайыз.
y=F(x) тізбексіздігі берілген arctg k (9.2-сурет, б),	бұрышының
шегінен шықпайтын болсын, яғни кез-келген х мəнінде
0< F(x)< kx.	(9.9)

35

Q(p) көпмүшесінің теріс нақты бөлікті түбірлері бар деп немесе олардан

басқа екіден	көп емес	нөлдік	түбірлері бар болсын. Басқаша						айтқанда Q(p)
мəнінде an = 0 немесе an		= 0 жəне an-1 = 0 болуына жол беріледі.
			W ( p) =		R( p)		.
					Q( p)
В. М. Попов	теоремасының		формулировкасын					келтіреміз: сызықтық		емес
жүйенің тұрақтылығын		орнату	үшінh			мəнін қою		жеткілікті,	ол мəн	барлық
w ³ 0 кезінде болуы керек.
	Re(1 + jwh)W ( jw) +			1		f 0 ,				(9.10)
				k

мұнда W (jw) - жүйенің сызықтық бөлігінің амплитудалық-фазалық жиіліктік сипаттамасы. Бір нөлдік плюс болғанда болуы керек,

ImW (jw)® -¥ болғанда w ® 0 ,

ал екі нөлдік плюс болғанда

ReW (jw)® -¥ болғанда w ® 0 , ал ImW (jw) p 0 аз болғанда w .

Теорема Q(p) сызықтық бөлiктің берiлiс функцияның бөлiмiнде екi таза жорамал түбiрлер болған жағдайда, бiрақ сонымен бiрге шектi орнықтылықтың шарты деп аталатын қосымша шарттар болғанда дұрыс болады.

9.3 – сурет. W * ( jw) графигі

Дəл осы теореманың ыңғайлы графикалық интерпретациясын беретін басқаша тұжырымы W * (jw)өзгертілген жиіліктік сипаттамасымен

байланысты. Ол келесі жолмен анықталады:

ReW	*	(jw) = ReW (jw),	ü
			ï	(9.11)
	*		ý
			ï
ImW (jw )= w ImW (jw .)þ

36

Q(p) жəне R(p) мəндерінде дəрежелер айырмашылығы п- т>1 болғанда W * ( jw) графигінің түрі W ( jw) (9.3 - сурет а), графигіне ұқсас болады. Егер де дəрежелер айырмашылығыn - m = 1 болса W * ( jw) (9.3 - сурет б) графигінің соңы жалған осьте координаттар басынан төмен орналасады.

Теңсіздіктің сол жағын түрлендіреміз (9.10):

Re(1 + jw h)W ( jw) + 1 = ReW ( jw) - w h ImW ( jw) + 1 .

k	k
Сонда, қойып
W * (jw) = U * (w)+ jV * (w)

жəне (9.11) қатынасын қолданып, В. М. Попов теоремасы үшін (9.10) орнына аламыз

	U * (w) - hV * (w) +	1		f 0		(9.11)
		k
	барлық уақытта w ³ 0 .
	Очевидно, что равенство
	U * (w) - hV * +			1	= 0	(9.12)
				k

теңдік W * (jw) жазықтығындағы теңдеуді көрсететіні анық.

Бұдан В.М.Попов теоремасының келесі графикалық интерпретациясы шығады: сызықтық емес жүйенің тұрақтылығын қамтамасыз ету үшін

W * (jw) жазықтығында (- 1 , j0) (9.4- сурет) нүктесі арқылы өтетін, k

барлық W * (jw) қисығы оң жағында қалатындай түзу жүргізу керек.

9.4-сурет. В.М. Попов теоремасының графикалық интерпретациясы

Негізгі əдебиеттер: 3 [324-348]. Қосымша əдебиеттер: 1 [365-414].

37

Бақылау сұрақтар:

1.Сызықты емес жүйелердiң абсолюттi орнықтылығының шарттары.

2.Қандай орнықтылықты абсолюттi орнықтылық деп атайды.

3.В.М.Поповоның жиiлiк əдiсi.

4.В.М.Попов критериясыi.

Дəрістің	тақырыбы: 10 Сызықты емес		АРЖ процесстеріндегі
орнықтылық
Дəріс конспектісі.		Сызықтық емес жүйелерде кей жағдайларда тек тепе-
теңдік жағдайлары ғана ,емессонымен қатар			белгілі	процесстердің
орнықтылығын анықтау да қызығушылық туғызады. Себебі жалпы жағдайда
орнықтылық тепе-теңдігі процесс орнықтылығымен			сəйкес келмеуі мүмкін.
Я.З. Цыпкин	Попов	белгісі процесстер орнықтылығын		зерттеуге де
бағытталуы мүмкін.
Өрнегімен анықталатын сызықтық емес жүйедегі мəжбүрлі процесстің
абсолютті орнықтылығын анықтаймыз.
		t
	xB (t) = f (t) - òk И (t -t )F[xB (t )]dt .			(10.1)

-¥

Интегралда айнымалыны тиiстi жолымен	алмастыру (10.1) арқылы
өрнекті түріне келтіруге болады.
¥
xB (t) = f (t) - òkИ (t )F[xB (t )]dt	(10.2 а)
0

Əсер етуші процесс бар жəнеt=0 моментінде жүйеге f1 (t) жоғалатын əсер қосылады деп есептейік. Сонда f1 (t) бұрын болған f(t)-ке түседі, ал

хв (t) процесі x (t ) вариациясын алады:

t
xB (t) + x(t )= f (t) + f1 (t )- òk И (t -t )F[xB (t ) + x(t )]dt	(10.3)

-¥

Ауытқушы процессті көрсететiн (10.3 ) теңдеулерден əсер етуші процесстiң (10.1 ) теңдеуiн аламыз жəне ауытқу үшiн теңдеу аламыз:

		t
	x (t )= f1 (t )- òk И (t -t )F0 [x(t ),t ]dt ,						(10.4)
	мұнда	-¥
			ìF[xB (t )+ x (t )]- F[xB (t )], t ³ 0, ü
	F0	[x(t ), t ]=					(10.5)
			í	t £	0.	ý
			î0,			þ

(10.5) жəне (10.2 а) ескере отырып (10.4) теңдеуін мына түрге келтіреміз:

38

t
x (t )= f1 (t )- òkИ (t -t )F0 [x(t ),t ]dt ,	(10.6)
0
Бұл теңдеулер Попов белгi iсшығарылған	теңдеуден F0 функциясы

уақытқа тəуелді болады. Сызықтық емес жүйе стационарлық емес сипаттамаға ие.

Келесі шарт дəлелденген: сыртқы шекті əсерден туындаған сызықтық емес жүйедегі процесс абсолютті тұрақты болуы үшін берілгенr кезінде түрленген сызықтық бөлік тұрақты жəнеW ( jw) сызықтық бөлігінің жиілік сипаттамасы

	Re	W ( jw)	+			1	³ 0		(0 £ w p ¥),	(10.7)
		1 + rW (jw ) K - r
шартын	қанағаттандырғаны,					ал		F(x)	сызықтық емес	сипаттамасының
туындысы
(r + e , K - e ), т. е. r + e £				dF(x)				£ K - e ,		(10.8)
						dx
мұнда e	- жолына тəуелді болғаны жеткілікті.

Сызықтық бөлік тұрақты болған жағдайда r = 0 деп алып аламыз

ReW (jw )+ 1 ³ 0 (0 £ w p ¥)

K

немесе

Re KW (jw)+1 ³ 0.

Геометриялық жағынан бұл K беріліс коэффиценті бар сызықтық емес элементті сызықтықпен алмастыру нəтижесінде алынатынKW (jw) ажыратылған сызықты жүйенің сипаттамасыV (w)= -1 түзуінің оң жағында немесе W ( jw) сипаттамасы V (w) = -1/ K түзуінің сол жағында жататынын білдіреді. (5.11 сурет.)

10.1- сурет. Ажыратылған	10.2 - сурет. Нолдік координат жүйесі
сызықтық жүйенің сипаттамасы

39

Жəне де сызықтық емес элемент сипаттамалар шарттын қанағаттандыруы керек

	0 p	F[x(t) + x (t)]- F[x(t)]	p K ,			(10.9)
		x(t)
	яғни сипаттама жаңа координаттар жүйесінің (01 , K1 ) секторында жатуы керек
	(10.2- сурет). 01 K1 көлбеулігі ОК көлбеулігіне тең болуы тиіс. Егер			0 p	dF1	(x)	p K
					d (x )

болса шарт орындалады. Ажыратылған сызықтық жүйе тұрақсыз не бейтарап болғанда жəне r нөлден бөлек болғанда болады

Re	KW (jw)	+	1	³ 0,	(10.10)
	A + KW (jw )		A -1

мұнда A = K белгіленген.

r

KW (jw) = U + jV болсын. Сонда (10.10)

теңсіздігін теңдікпен алмастыра

отырып ішіне KW (jw) сипаттамасы

кірмейтін

облыс шекарасы теңдеуін

аламыз.

U + jV

1

+

= 0,

A +U + jV

ол түріне алып келуі мүмкін

A -1

æ

A +1ö

2

2

æ A

-1ö2

(10.11)

çU

+

÷

+V

= ç

÷ .

è

2 ø

è

2 ø

(10.11 ) теңдеуі орталығы терiс нақты жарты өсi үстiнде жатқан жəне (-1, j0) ортақ жанасу нүктелері бар дөңгелектер жиынын анықтайды.

10.3- сурет. Абсолютті орнықтылық	10.4 - сурет. Геометриялық интерпретация
критериінің геометриялық интерпретациясы

Дөңгелектерiнiң жиыны тұйық жүйенің заттық жиілік сипаттамасының ординаталарының тең мəндері үшін құрылған дөңгелек диаграммаларды құрғандағыдай болатынын байқау қиын емес.

40